気になる超楕円曲線 - ryamadaのコンピュータ・数学メモ

まずはWikipedia
$y^2 = f(x)$ なる(x,y)らしい
Rで書く

x <- seq(from=-4,to=4,length=100000)
fx <- x * (x+1) *(x-3) * (x+2) * (x-2)
y1 <- y2 <- rep(NA,length(x))
s <- which(fx>=0)
y1[s] <- sqrt(fx[s])
y2[s] <- -y1[s]

plot(c(x,x),c(y1,y2),type="l")

my.draw.hyperepilleptic <- function(x,f,draw.f=FALSE){
	fx <- f(x)
	y1 <- y2 <- rep(NA,length(x))
	s <- which(fx>=0)
	y1[s] <- sqrt(fx[s])
	y2[s] <- -y1[s]
	plot(c(x,x),c(y1,y2),type="l")
	if(draw.f){
		points(x,fx,type="l",col=2)
	}
}
f <- function(x){
	x * (x+1) *(x-3) * (x+2) * (x-2)
}
my.draw.hyperepilleptic(x,f,TRUE)

楕円曲線と超楕円曲線っていうのは、(x,y)平面に描いたときに、重ならない輪が並んだような絵を描く曲線(ただし、無限遠点でようやく閉じる輪も許す)
この楕円曲線(超楕円曲線)上の点を「数」とすると、それらには、幾何的な関係で表現できる演算があって、いい感じに群論的に扱える。たとえば、点Pと点Qとから、点Rを作るルールを乗せられる。そのときに、「基準点〜単位元相当の点」というのもあるし・・というような
これを曲線の有理点の個数問題として考えることもあるらしい。どうしてか、というと、上で書いた「点の間のルール」というのが、平面上の直線で構成するのだが、直線というのは、加減乗除で計算してその交点とかを書き表せるが、それって初期点座標が「有理数の点」なら、そのルールでできる点は全部有理数の点になる、ということになるから、二次元実平面上の有理点だけを扱うことができてくる。その個数の問題とかがあるらしい
一方(これが一方なのか、有理点問題と同じことなのかはわかっていないのだけれど)、写像類群で出てくるのは、輪が並んでいるときに、「輪が消えて〜実世界から虚世界に移行して」行き、また「実世界に戻ってくる」と見ることができるのだが、その「虚実移行」が「点」になっているけれど、そこが、穴のある曲面上で自由に移行できない円の切り替え操作に相当する、という関係になるらしい
$y^2=f(x)$ というのは標準的な形で、一般的な形というのは $y^2+h(x)y=f(x)$ となる
このあたりはRで描き分けるのが有効なので、少し丁寧になぞってみる
$y^2=f(x)$ というのは、 $y=\pm\sqrt{f(x)}$ と言うように、x軸に関して上下対称な曲線になる
そして、曲線が実数世界で「現れる」のは、 $f(x) \ge 0$ を満足するxについてである
他方 $y^2+h(x)y=f(x)$ というときには、 $(x,y)=(a,b)$ がこの曲線上の点であるとすると $(x,y)=(a,-b-h(a))$ も曲線上の点である
$x=a$ における曲線上の２点の中点は、 $(x,y)=(a,(b)+(-b-h(a))/2)=(a,-h(a)/2)$ であることがわかる
また $y^2=f(x)$ のときに、実数世界で曲線が現れた範囲は $f(x) \ge 0$ を満足する範囲であったが、 $y^2+h(x)y=f(x)$ での『判別式』は $h(x)^2+4f(x) \ge 0$ であることがわかり、 $h(x)^2+4f(x)=0$ の解との関係となることがわかる
今 $f(x)=0,h(x)=0$ を $a\prod_{i=1}^k (x-x_i)$ という多項式で表すことにする(実解がk個あるk次多項式であるということだが)。複素数解も、と言うことであれば、共役複素数をペアで与えることでもよいが、今は、実解k個にしておく
xはx座標、xsはk個の実解、aは定数倍係数とすれば、以下のようにすることで、xs,aにて多項式を与え、そのxにおける値を計算することができる

my.make.polyfx <- function(x,xs,a=1){
	if(length(xs)==0){
		return(rep(0,length(x)))
	}
	m <- matrix(rep(x,length(xs)),ncol=length(xs))
	m <- t(t(m)-xs)
	apply(m,1,prod)*a
}

これを使って、適当にf(x),h(x)を与えて超楕円曲線を描いてみよう。ただし、f(x)の次数とh(x)の次数には、h(x)の次数の２倍がf(x)の次数と比べて大きすぎないことが超楕円曲線の定義になっている。なぜなら、h(x)の次数がそれより大きいと、 $h(x)^2+4f(x)=0$ の解の『主導者』がf(x)からh(x)に交代してしまって、超楕円曲線の両端の輪が無限遠に行っても閉じなくなるから…無限遠で閉じることについては、さらに、以降で射影同次座標を使って無限遠点を取り込むことで、R的に描図するが、まずは、超幾何曲線を普通に描いておく
曲線のy軸方向での「中点」を結ぶ曲線や、判別式曲線と超楕円曲線の閉じている点、太り・痩せの具合などを確認しよう

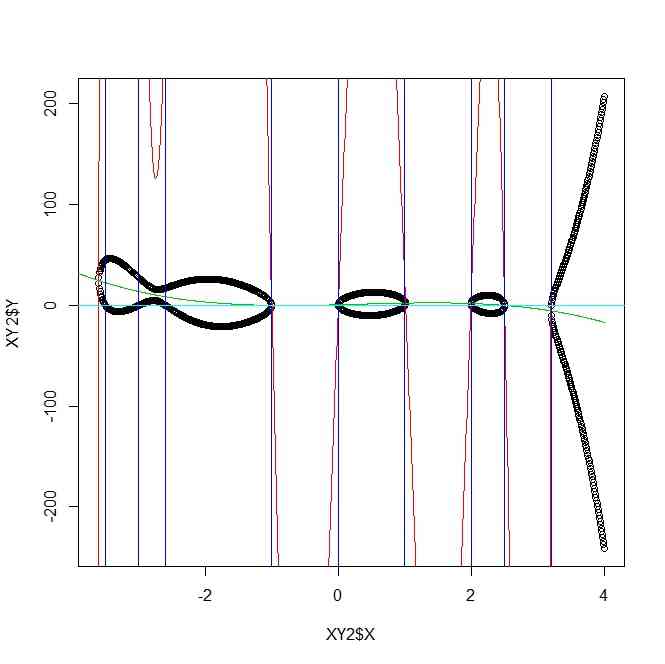
XY <- my.coord.hyperepilleptic(x,f,h)
fxs <- list(c(-3.5,-3,-2.6,-1,0,1,2,2.5,3.2),1)
hxs <- list(c(-1,-0.5,2.5),1)
#hxs <- list(c(),1)
XY2 <- my.coord.hyperepilleptic2(x,fxs,hxs)
F <- my.make.polyfx(x,fxs[[1]],fxs[[2]])
H <- my.make.polyfx(x,hxs[[1]],hxs[[2]])
degF <- length(fxs[[1]])
degH <- length(hxs[[1]])
degF
degH

plot(XY2$X,XY2$Y)
points(x,H^2+4*F,col=2,type="l")
points(x,-H/2,col=3,type="l")
abline(v=fxs[[1]],col=4)
abline(h=0,col=5)

超楕円曲線では、無限遠点で閉じていることが特徴(らしい)が、それを実感するには、無限遠点を「わかりやすい世界」に持ってくるのがよい
射影幾何を使って、持ってくることにする
射影幾何では(x,y)という二次元座標を(X=x/1,Y=y/1,Z=1)とみなした上で、Zを自由にし、(X,Y,Z)という３次元座標を(X/Z,Y/Z)という二次元座標みなす「同次座標」を使う。これを使うとZ=0という点は二次元的には無限遠点に相当するが(0,1,0)のような３次元の有限な座標で表すことができる
$y^2+h(x)y=f(x)$ の $(x,y)$ を、 $x=X/Z,y=Y/Z$ と考えれば $(Y/Z)^2 + h(X/Z)=f(X/Z)$ となる。ここで分母に来ているZを全部なくすために、h(x),f(x)の次数の大きい方の次数k(それはf(x)の次数だが)の分である $Z^k$ 倍すれば、 $(Y/Z)^2Z^k + h(X/Z)Y/Z Z^k =f(X/Z) Z^k$ と言う、 $(X,Y,Z)$ の方程式ができる
単純な例で見てみる(f(x)の次数が３なので『超』ではないが)

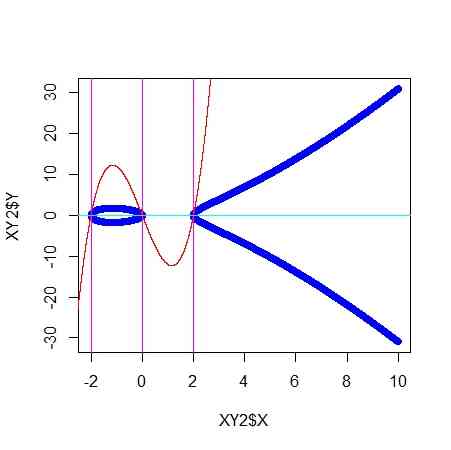
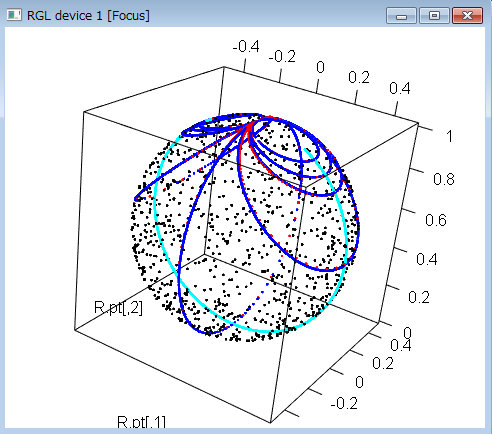
(超)楕円曲線(青)と、それを決める判別式曲線(赤)、y=0の直線(水色)などを二次元と三次元とで描いている
三次元で、混んでいるのは、無限遠のあたり、三次元でスカスカしているところは原点周辺
確かに、判別式曲線とy=0との交点を(超)楕円曲線も通っている
大きい青い輪が原点付近の実二元座標でも閉じている輪で、小さい青い輪は、二次元では開いているが、三次元では無限遠で閉じているのがわかる

# 二次元座標を中心(0,0,0.5)で半径0.5の球面に写す関数
# 原点(0,0)は(0,0,0)へ、無限遠は(0,0,1)に写る
my.projective.sphere <- function(X){
	R <- sqrt(apply(X^2,1,sum))
	theta <- atan(R) * 2
	z <- -0.5 * cos(theta) + 0.5
	r <- 0.5 * sin(theta)
	cbind(X/R * r,z)
}
library(rgl)

x <- seq(from=-10,to=10,length=100000)

fxs <- list(c(-2,0,2),1)
hxs <- list(c(),1)
#hxs <- list(c(),1)
XY2 <- my.coord.hyperepilleptic2(x,fxs,hxs)
F <- my.make.polyfx(x,fxs[[1]],fxs[[2]])
H <- my.make.polyfx(x,hxs[[1]],hxs[[2]])

plot(XY2$X,XY2$Y,col=4)
points(x,H^2+4*F,col=2,type="l")
points(x,-H/2,col=3,type="l")
abline(v=fxs[[1]],col=6)
abline(h=0,col=5)

XYZ <- my.projective.sphere(cbind(XY2$X,XY2$Y))

HF.z <- my.projective.sphere(cbind(x,H^2+4*F))
H.z <- my.projective.sphere(cbind(x,-H/2))
zero.z <- my.projective.sphere(cbind(x,rep(0,length(x))))
n.pt <- 10^3
R.pt <- matrix(rnorm(n.pt*3),ncol=3)
R.pt <- R.pt/sqrt(apply(R.pt^2,1,sum))
R.pt <- R.pt/2
R.pt[,3] <- R.pt[,3] + 0.5

plot3d(R.pt)

points3d(XYZ,col=4)
points3d(HF.z,col=2)
#points3d(H.z,col=3)
points3d(zero.z,col=5)

少し複雑に

x <- seq(from=-4,to=4,length=100000)

fxs <- list(c(-3.5,-3,-2.6,-1,0,1,2,2.5,3.2),1)
hxs <- list(c(-1,-0.5,2.5),1)
#hxs <- list(c(),1)
XY2 <- my.coord.hyperepilleptic2(x,fxs,hxs)
F <- my.make.polyfx(x,fxs[[1]],fxs[[2]])
H <- my.make.polyfx(x,hxs[[1]],hxs[[2]])

plot(XY2$X,XY2$Y,col=4)
points(x,H^2+4*F,col=2,type="l")
points(x,-H/2,col=3,type="l")
abline(v=fxs[[1]],col=6)
abline(h=0,col=5)


XYZ <- my.projective.sphere(cbind(XY2$X,XY2$Y))

HF.z <- my.projective.sphere(cbind(x,H^2+4*F))
H.z <- my.projective.sphere(cbind(x,-H/2))
zero.z <- my.projective.sphere(cbind(x,rep(0,length(x))))
n.pt <- 10^3
R.pt <- matrix(rnorm(n.pt*3),ncol=3)
R.pt <- R.pt/sqrt(apply(R.pt^2,1,sum))
R.pt <- R.pt/2
R.pt[,3] <- R.pt[,3] + 0.5

plot3d(R.pt)

points3d(XYZ,col=4)
points3d(HF.z,col=2)
#points3d(H.z,col=3)
points3d(zero.z,col=5)