準結晶 cut & project 再び

• 移動の評価から準結晶に戻ってきた
• 昨日もcut ' projectで…ということを書いたが、やはり、cut & projectやそれと黄金比の関係をRレベルでハンドリングできないと…ということでやってみる
• 参考サイト,参考サイト2
• まずは、１次元フィボナッチ格子を２次元正方格子における傾き=黄金比でのcut & projectでやってみる
• 傾き=黄金比の帯を描くことと、その傾き分の回転をしてその上で水平な帯を引くことは同じだが、そんなことをRで。
• 回転前の帯

• 回転後の帯

• 選ばれた点の写像

# 正方格子を作る
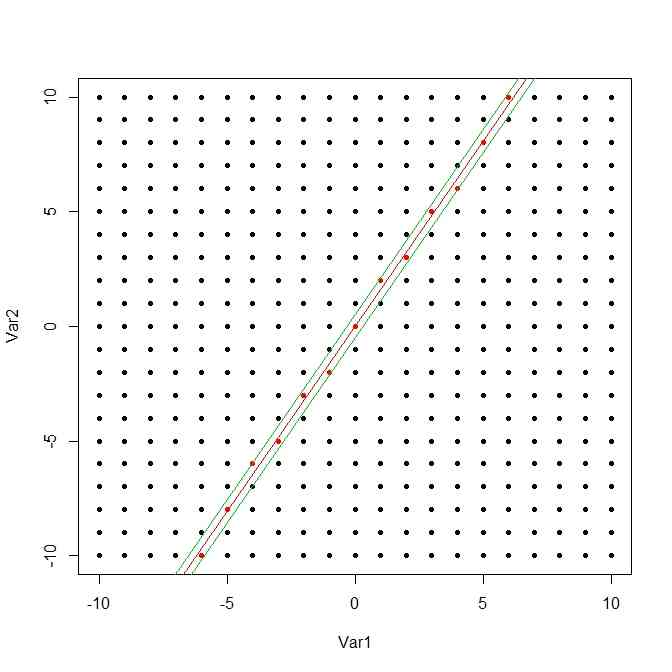
x <- (-10):10
xy <- expand.grid(x,x)
# 黄金比
golden.ratio <- (1+sqrt(5))/2
# 黄金比の傾きの帯上の点を取り出す
s <- which(abs(golden.ratio*xy[,1]-xy[,2])<0.5)
# 色分け
my.col <- rep(1,length(xy[,1]))
my.col[s] <- 2
plot(xy,pch=20,col=my.col)
abline(0,golden.ratio,col=2)
abline(0.5,golden.ratio,col=3)
abline(-0.5,golden.ratio,col=3)
# 黄金比の傾き分回転する
theta <- atan(golden.ratio)
rot <- matrix(c(cos(theta),-sin(theta),sin(theta),cos(theta)),2,2)
xy.rot <- t(rot %*% t(xy))
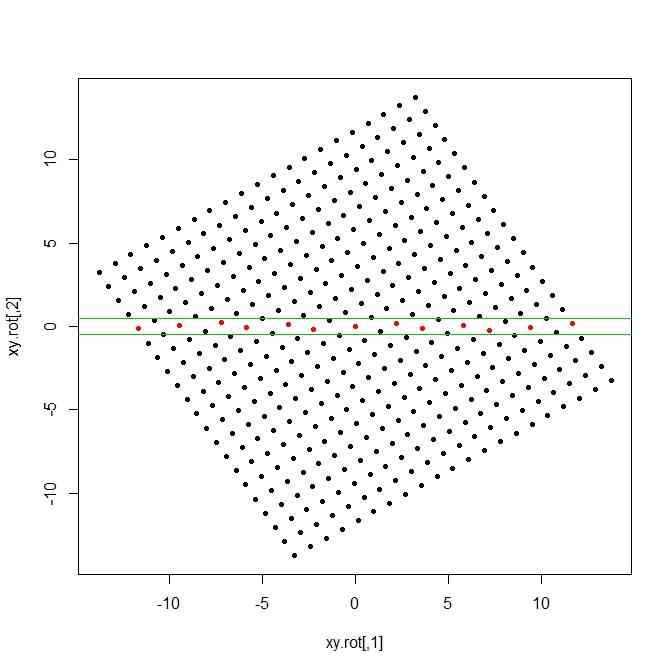
plot(xy.rot,pch=20,col=my.col)
abline(h=c(0.5,-0.5),col=3)
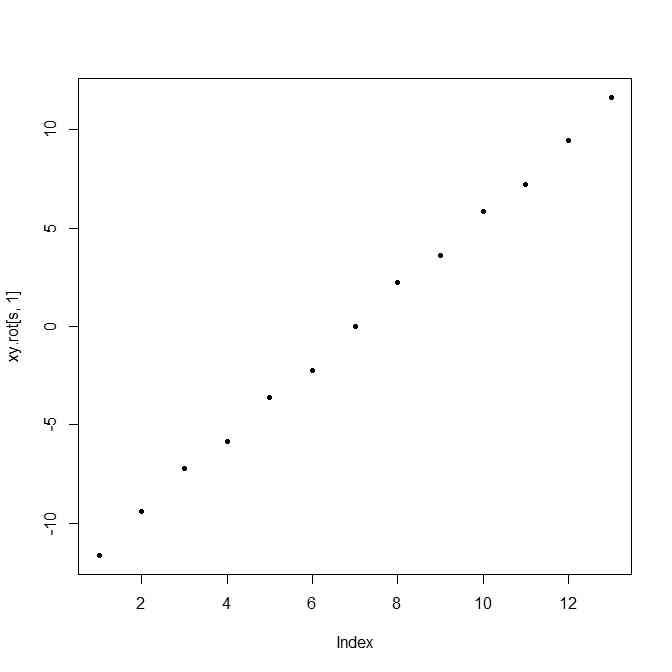
plot(xy.rot[s,1],pch=20)

• ４次元の結晶を…(ちょっと違うんだなー)

t <- 0:3
X <- cbind(cos(t/6*pi),sin(t/6*pi),cos(5*t/6*pi),sin(5*t/6*pi))
plot(X[,1:2])
x <- (-10):10
xy <- as.matrix(expand.grid(rep(list(x),4)))
#d <- as.matrix(dist(xy,method="manhattan"))
#s <- which(d==1,arr.ind=TRUE)
z <- xy %*% X
ss <- which(sqrt(apply(z[,3:4]^2,1,sum))<0.5)
z.ss <- z[ss,]
xy.ss <- xy[ss,]
ed <- matrix(0,length(xy.ss[,1]),length(xy.ss[,1]))
for(i in 1:(length(ed[,1])-1)){
	for(j in (i+1):length(ed[,1])){
		if(max(abs(xy.ss[i,]-xy.ss[j,]))<2){
			ed[i,j] <- 1
		}
	}
}
s <- which(ed == 1,arr.ind=TRUE)
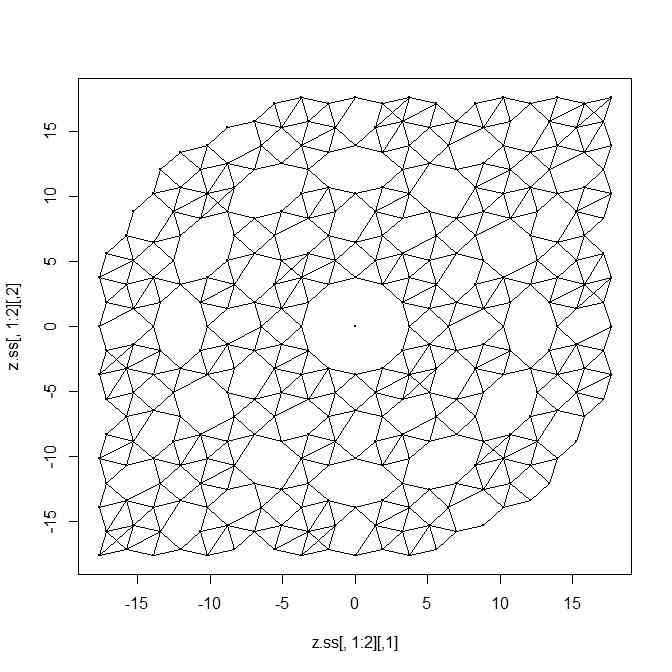
plot(z.ss[,1:2],pch=20,cex=0.2)
segments(z.ss[s[,1],1],z.ss[s[,1],2],z.ss[s[,2],1],z.ss[s[,2],2])