指数関数で複素平面を閉じる
- 複素平面の虚軸という直線は、指数関数変換をすると複素単位円に写る
- 今、虚部が非負の複素半平面上に原点を出発する曲線があったとする
- これを指数変換すると、曲線が虚軸と交差する点は複素単位円に写され、実部負の点は単位円の内部に、実部正の点は単位円の外部に写される
- ここで、複素半平面上の曲線が、原点を出発し、虚軸上の点
で終わるとすると、この曲線は、閉曲線となる
- SLE曲線の離散版Schwarz-Christoffel(こちら)を使うこともできる
- この考えで行くと、少し注意が必要。複素数(複素平面)の指数関数は、円板が無限層に重なり合った構造をしている→こちらなわけなので、実は、虚部について0-2piで実部は正負無限大の帯が複素平面に対応づく。それを考慮すると、複素上半平面は、虚部について2piの周期でぐるぐる円柱巻きにしたうえで、その上に曲線が描かれる。そのうえで、「交差することなく」実部０、虚部2pi(もしくは0)に戻ると、その指数関数変換によって、交差のない曲線が、複素平面全体に描けたことになる
- 複素数の指数関数変換については、色塗りをしたい(一つは複素数によって明度と彩度を指定する方法、もう一つは市松模様にする方法)
t <- seq(from=0,to=1,length=10001)*3*pi x <- 1i * t X <- cos(t) - t^0.5 Y <- t x <- X + 1i * Y plot(x,type="l",asp=TRUE) y <- exp(x) plot(y,type="l",asp=TRUE) my.schwarzChristoffel <- function(p,n,S0=0+0*1i,p2 = NULL){ if(is.null(p2)){ p2 <- p } rw <- sample(c(-1,1),n,replace=TRUE) * runif(n,min=p,max=p2) + 1/2 + 0 * 1i my.S <- function(z,a){ z <- z + 0*1i (z+2*sqrt((1-a)/a))^(1-a)*(z-2*sqrt(a/(1-a)))^a } S0 <- 0 + 0 * 1i Ss <- rep(0,n) for(i in 1:n){ if(i == 1){ Ss[i] <- my.S(S0,rw[i]) }else{ Ss[i] <- S0 for(j in i:1){ Ss[i] <- my.S(Ss[i],rw[j]) } } } Ss } ps <- seq(from=0.05,to = 0.45,length=3) ps <- 0.0 ps2 <- 0.1 n.iter <- 1 n <- 2000 out <- matrix(0,length(ps)*n.iter,n) cnt <- 1 col <- c() for(i in 1:length(ps)){ for(j in 1:n.iter){ out[cnt,] <- my.schwarzChristoffel(ps[i],n,p2=ps2[i]) cnt <- cnt + 1 col <- c(col,i) } } out <- cbind(rep(0,n.iter),out) plot(out[1,],type="l",xlim = range(Re(out)),ylim=range(Im(out)),col=col[1]) for(i in 2:length(out[,1])){ points(out[i,],type="l",col=i) } exp.out <- exp(out/max(Re(out),Im(out))) plot(exp.out[1,],type="l",xlim = range(Re(exp.out)),ylim=range(Im(exp.out)),col=col[1]) for(i in 2:length(exp.out[,1])){ points(exp.out[i,],type="l",col=i) } # 終末点を i * 2 * piにする #exp.out.2 <- out/Mod(out[,length(out[1,])]) 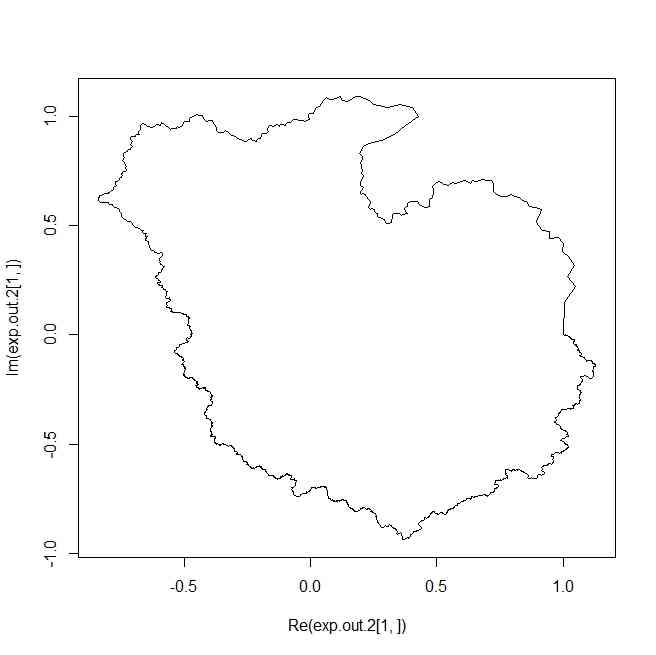out.2 <- out/out[,length(out[1,])] * 1i * 2 * pi exp.out.2 <- exp(out.2) plot(exp.out.2[1,],type="l",xlim = range(Re(exp.out.2)),ylim=range(Im(exp.out.2)),col=col[1]) for(i in 2:length(exp.out.2[,1])){ points(exp.out.2[i,],type="l",col=i) }
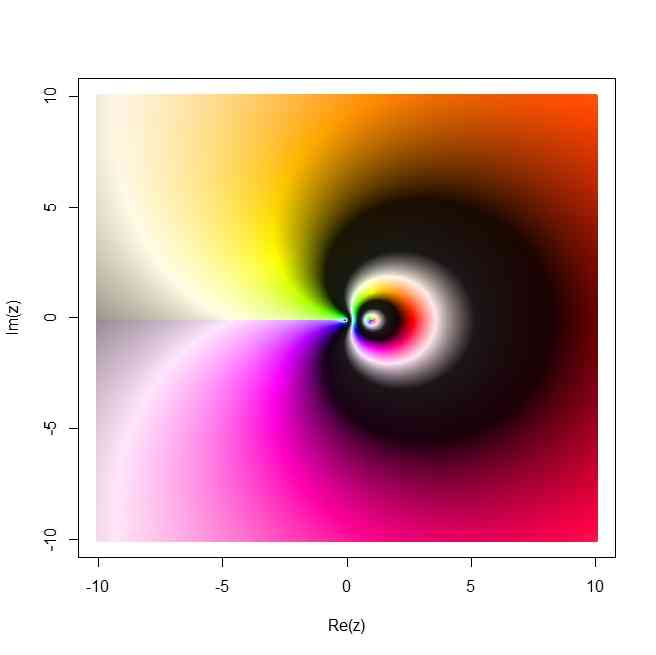
my.complex.color <- function(z,int0=0.6,sat0=0.3,int1=1,sat1=1){ my.hsv <- function(z,int0=0.6,sat0=0.3,int1=1,sat1=1){ # 複素数の偏角 arg <- Arg(z) s <- which(arg<0) arg[s] <- arg[s]+2*pi # 複素数の絶対値 r <- Mod(z) # 絶対値が非常に大きくてもそこそこの色になるように対数変換 s <- which(r>1) r[s] <- log(r[s]) # 絶対値で周期性が出るように4のmod r. <- 4*(r%%1) k <- floor(r.) r. <- r.-k # 明度が上限、明度が下限、彩度が上限、彩度が下限の４パターンを # 4のmodに対応づける # 明度・彩度を動かすときは、複素数の絶対値で１次線形変化 inten <- sat <- rep(0,length(r)) s <- which(k==0) inten[s] <- int1 sat[s] <- sat1-(sat1-sat0)*r.[s] s <- which(k==1) inten[s] <- int1-(int1-int0)*r.[s] sat[s] <- sat0 s <- which(k==2) inten[s] <- int0 sat[s] <- sat1-(sat1-sat0)*(1-r.[s]) s <- which(k==3) inten[s] <- int1-(int1-int0)*(1-r.[s]) sat[s] <- sat1 return(cbind(arg,inten,sat)) } my.hsv2rgb <- function(h,s,v){ # 色相の6 のmodでぐるりの情報を作る hi <- floor(h/(2*pi)*6) hi[which(hi==6)] <- 0 # 色相のぐるりの余りをfに入れ、それと明度・彩度とでp,q,tという３変数を決める # ３変数を色相からの値を取らせる１つの原色を除いた２原色の値を定めるために使う # 使い方は巡回させることでうまいことやる f <- (h/(2*pi)*6) %%1 p <- v*(1-s) q <- v *(1-f*s) t <- v *(1-(1-f)*s) r <- g <- b <- rep(0,length(h)) s <- which(hi==0) r[s] <- v[s];g[s] <- t[s]; b[s] = p[s]; s <- which(hi==1) r[s] <- q[s];g[s] <- v[s]; b[s] = p[s]; s <- which(hi==2) r[s] <- p[s];g[s] <- v[s]; b[s] = t[s]; s <- which(hi==3) r[s] <- p[s];g[s] <- q[s]; b[s] = v[s]; s <- which(hi==4) r[s] <- t[s];g[s] <- p[s]; b[s] = v[s]; s <- which(hi==5) r[s] <- v[s];g[s] <- p[s]; b[s] = q[s]; return(cbind(r,g,b)) } hsv <- my.hsv(z,int0=int0,sat0=sat0,int1=int1,sat1=sat1) col <- my.hsv2rgb(hsv[,1],hsv[,3],hsv[,2]) rgb(col[,1],col[,2],col[,3]) } x <- seq(from=0,to=2*pi,len=1000) xx <- expand.grid(x,x) z <- xx[,1]+1i * xx[,2] log.z <- log(z) plot(z,col=my.complex.color(log.z,0.1,0.1,1,1),pch=20) plot(exp(z),col=my.complex.color(z,0.5,0.5,1,1),pch=20,xlim=c(-3,3),ylim=c(-3,3)) plot(z,col=my.complex.color(z,0.1,0.1,1,1),pch=20,xlim=c(-20,20),ylim=c(-20,20)) 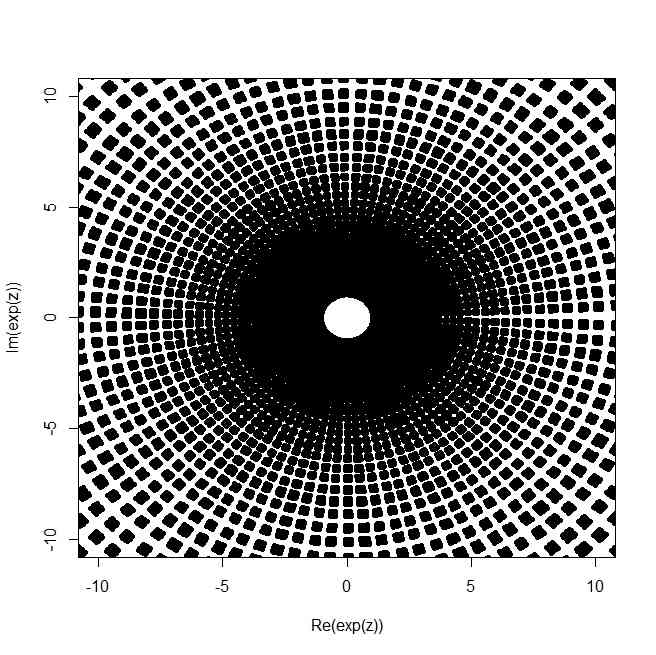col2 <- floor((Re(z)*30) %% 2) * floor((Im(z)*30) %% 2) plot(z,col=col2,pch=20) plot(exp(z),col=col2,pch=20,xlim=c(-10,10),ylim=c(-10,10))
