曲面の共形変換
- 共形変換は「角度を保存する変換」
- 直交する２直線は直交する
- 平面を３次元空間に埋め込んで２次元多様体をつくるときに、それが共形変換になっているというのは
- 平面の各点の法線ベクトル(これらは平面ならすべて同じ)が、埋め込み後に滑らかなベクトル場になっていることになる
- なぜならば、局所において直角が直角を保つということは、平面局所で接平面方向のベクトルとそれを接平面内で９０度回転したベクトルとが、埋め込み先でも同じようになっていることであるが
- それは、局所での法線ベクトル周りの９０度回転変換が、埋め込み先でも、法線ベクトル回りの９０度回転変換であることであって
- この法線ベクトルの９０度回転は(向きにも気を付ければ)、法線ベクトルのみで決まるものであるから
- 結局そのような変換は法線ベクトル方向さえ決めればきまり
- それが滑らかだということは滑らかなベクトル場であるということ
- 平面から出発したが、平面からの共形変換埋め込み１と、同じく平面からの共形変換埋め込み２との間には、法線ベクトル場１から法線ベクトル場２への対応付けをとればよいことから、平面はなくてもよい
- 法線ベクトル場を考えるとき、「法線ベクトル」は単位球面上の点の位置ベクトルであることにも注意
- また法線ベクトル場で、その変化を考えるとき、その変化量はすべて接平面成分であることにも注意
- また接平面上のベクトル場の埋め込み後の変化は、接平面上での変化成分と、法線方向成分での変化成分にきれいに分けられることも便利
- 埋め込みに伴う法線ベクトルの変化量と接平面の変化量との量的関係が曲率
- たとえば：
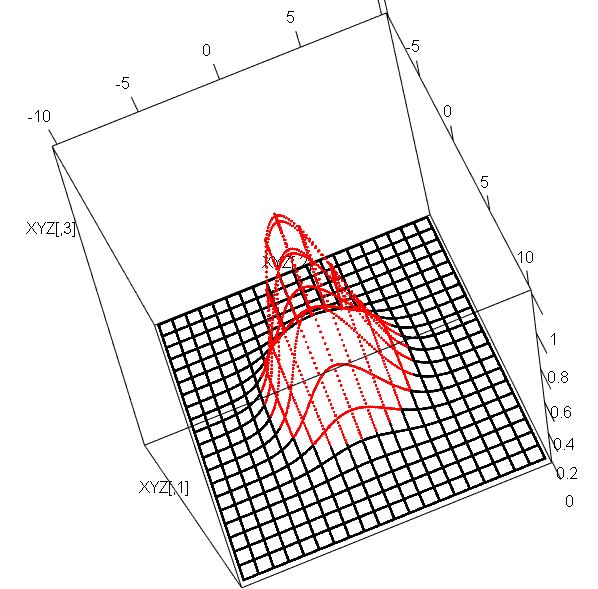
- 上から、平面グリッド、その曲面埋め込み、そして単位法線ベクトルの場
# xy二次元平面のグリッド点を作る x1 <- y1 <- seq(from=-10,to=10,length=21) x2 <- y2 <- seq(from=-10,to=10,length=201) xy <- rbind(expand.grid(x1,y2),expand.grid(x2,y1)) # ハンドリングしやすいようにその複素数版も作り xy. <- xy[,1] + 1i*xy[,2] # グリッドをプロット plot(xy,pch=20,cex=0.1) # わかりやすいように、ある特定領域の色を変えてプロット col <- rep(1,length(xy[,1])) col[which(Mod(xy.)<5)] <- 2 plot(xy,pch=15,col=col,cex=1) # これを滑らかに３次元曲面として埋め込む # 適当な関数でｚ座標を決めて曲面化する XYZ <- matrix(0,length(xy[,1]),3) r <- sqrt((xy[,1]-5)^2+(xy[,2]+3)^2)^1 r <- Mod(xy.) XYZ[,1] <- r*cos(Arg(xy.)) XYZ[,2] <- r*sin(Arg(xy.)) XYZ[,3] <- exp(-0.1*(Mod(xy.)^2)) plot3d(XYZ,col=col) plot3d(XYZ[which(col==2),],col=2) # その単位法線ベクトルを、元の２次元平面の点ごとに並べてプロットすれば # 単位法線ベクトル(なので球面に並ぶ)が滑らかに変化している様子がわかる # このように単位法線ベクトルが滑らかな場を作ることと、曲面への埋め込みが共形変換であることとの関係を述べたのが、この記事の説明部分 N <- cbind(-2*0.1*xy[,1]*exp(-0.1*Mod(xy.)),-2*0.1*xy[,2]*exp(-0.1*Mod(xy.)),1) N <- N/sqrt(apply(N^2,1,sum)) N. <- rbind(N,rbind(c(1,1,1),c(-1,-1,-1))) plot3d(N.,col=c(col,1,1))
