遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

京都大学学部入試数学問題2017で学ぶR

数学 高校数学 R
  • 昨日は国立大学(前期)入学試験の初日。京都大学でも国語と数学の試験がありました。
  • こちらに数学の試験問題(と解答)があります
  • 解説はお任せするとして、Rの練習課題として扱ってみましょう
  • （１）複素数と複素数での変換の話
    • 題意の通りにプロットしてみます


# [1]
## (1)
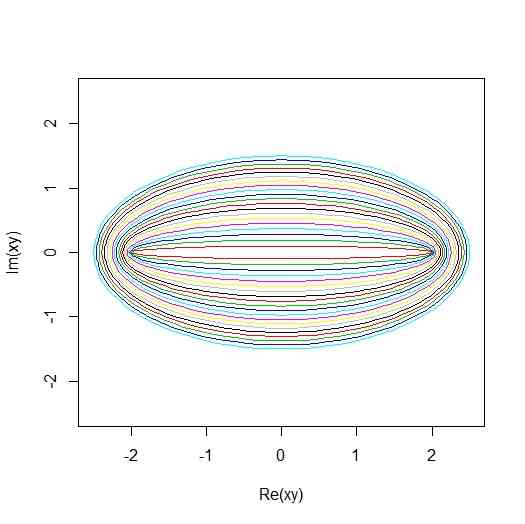
R <- 2
thetas <- seq(from=0,to=2*pi,length=101)
#thetas <- thetas[-1]

ws <- R * cos(thetas) + R * 1i * sin(thetas)
xy <- ws + 1/ws
xlim <- ylim <- range(c(Re(xy),Im(xy)))

plot(xy,type="l",xlim=xlim,ylim=ylim)

Rs <- seq(from=1,to=2,length=21)
Rs <- Rs[-1]
for(i in 1:length(Rs)){
	R <- Rs[i]
	ws <- R * cos(thetas) + R * 1i * sin(thetas)
	xy <- ws + 1/ws
	xlim <- ylim <- range(c(Re(xy),Im(xy)))
	points(xy,type="l",xlim=xlim,ylim=ylim,col=i+1)

}

## (2)

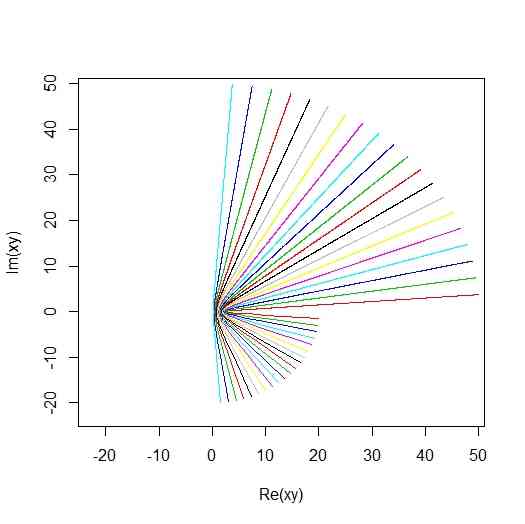
alpha <- pi/3
Rs <- seq(from=0,to=50,length=1000)
Rs <- Rs[-1]
ws <- Rs * cos(alpha) + Rs * 1i * sin(alpha)
xy <- ws + 1/ws

xlim <- ylim <- range(c(Re(xy),Im(xy)))
xlim[1] <- xlim[1]-5
xlim[2] <- xlim[2]+5
ylim[1] <- ylim[1]-5
ylim[2] <- ylim[2]+5

plot(xy,type="l",xlim = xlim,ylim=ylim)

alphas <- seq(from=0,to=pi/2,length=22)
alphas <- alphas[-1]
alphas <- alphas[-length(alphas)]

for(i in 1:length(alphas)){
	alpha <- alphas[i]
	ws <- Rs * cos(alpha) + Rs * 1i * sin(alpha)
	xy <- ws + 1/ws
	points(xy,type="l",col=i+1)
}
  • （２）３次元の図形。ベクトル。座標の自由度など
    • 平行になること、斜めになること、きれいな正八面体になること



# [2]
# O: X[1,]
# A: X[2,]
# B: X[3,]
# C: X[4,]
# D: r[1] * X[1,] + (1-r[1]) * X[2,]
# E: r[4] * X[2,] + (1-r[4]) * X[3,]
# F: r[6] * X[3,] + (1-r[6]) * X[4,]
# G: r[3] * X[4,] + (1-r[3]) * X[1,]
# H: r[2] * X[1,] + (1-r[2]) * X[3,]
# I: r[5] * X[2,] + (1-r[5]) * X[4,]

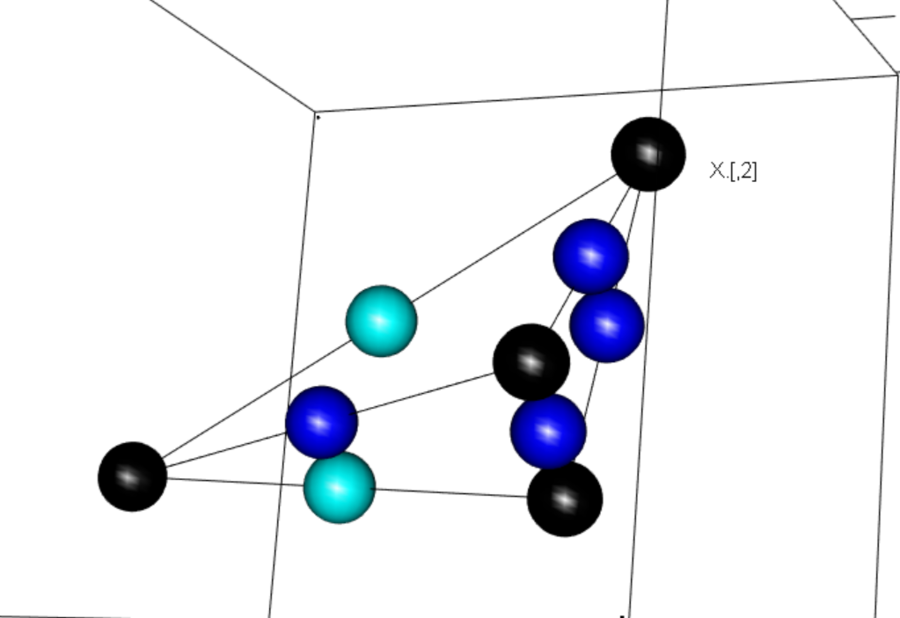
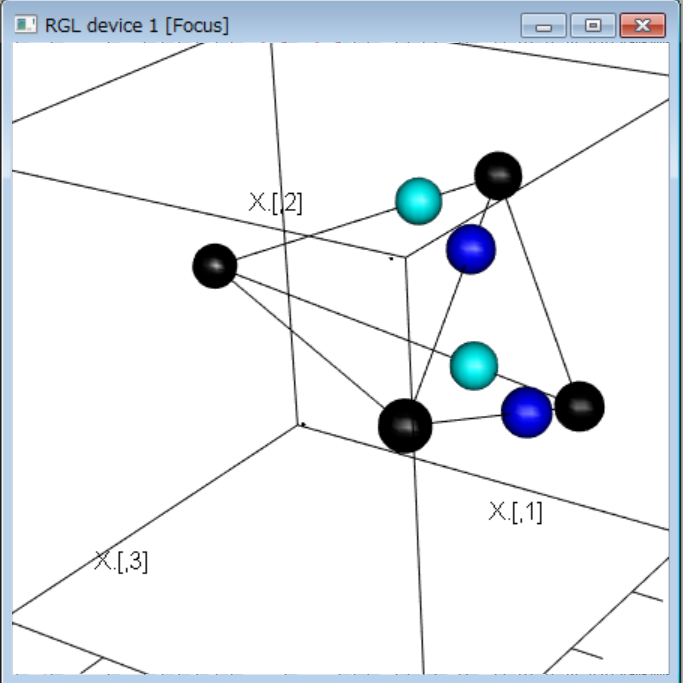
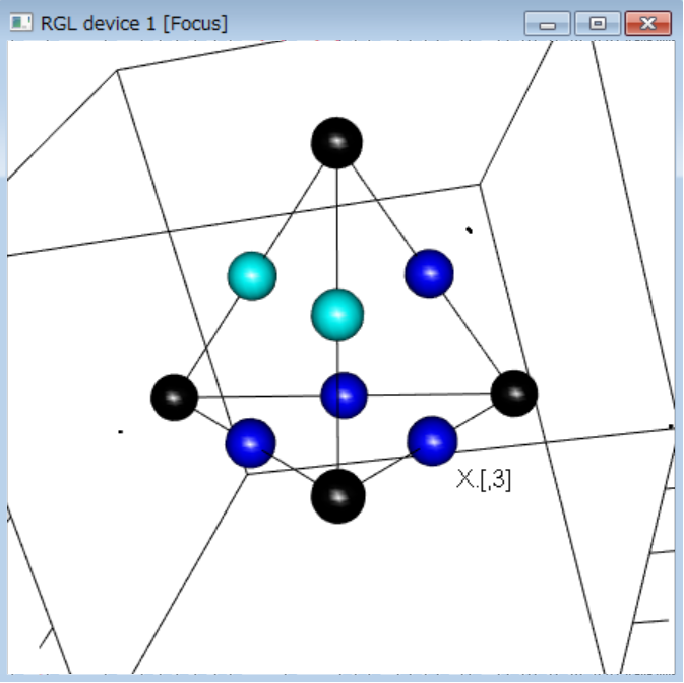
X <- matrix(rnorm(3*4),ncol=3)
X <- X/sqrt(apply(X^2,1,sum))
X. <- rbind(X,c(1,1,1))
X. <- rbind(X.,c(-1,-1,-1))
library(rgl)
plot3d(X.,)
spheres3d(X,radius=0.1)
r <- runif(6)
cnt <- 1
for(i in 1:3){
	for(j in (i+1):4){
		segments3d(X[c(i,j),])
		tmp <- X[i,] * r[cnt] + X[j,] * (1-r[cnt])
		spheres3d(tmp,color=2,radius=0.1)
		cnt <- cnt+1
	}
}

## (1)
r2 <- r
r2[1] <- r2[3]
r2[4] <- 1-r2[6]

cnt <- 1
for(i in 1:3){
	for(j in (i+1):4){
		segments3d(X[c(i,j),])
		tmp <- X[i,] * r2[cnt] + X[j,] * (1-r2[cnt])
		spheres3d(tmp,color=3,radius=0.1)
		cnt <- cnt+1
	}
}

O <- X[1,]
A <- X[2,]
B <- X[3,]
C <- X[4,]
D <- r2[1] * X[1,] + (1-r2[1]) * X[2,]
E <- r2[4] * X[2,] + (1-r2[4]) * X[3,]
F <- r2[6] * X[3,] + (1-r2[6]) * X[4,]
G <- r2[3] * X[1,] + (1-r2[3]) * X[4,]
H <- r2[2] * X[1,] + (1-r2[2]) * X[3,]
I <- r2[5] * X[2,] + (1-r2[5]) * X[4,]
plot3d(X.,)
for(i in 1:3){
	for(j in (i+1):4){
		segments3d(X[c(i,j),])
		tmp <- X[i,] * r2[cnt] + X[j,] * (1-r2[cnt])
	}
}
spheres3d(X,radius=0.1)
spheres3d(D,radius=0.1,col=4)
spheres3d(G,radius=0.1,col=4)
spheres3d(E,radius=0.1,col=5)
spheres3d(F,radius=0.1,col=5)

DG <- G-D
EF <- F-E
DG/EF


## (2)

r2 <- rep(1/2,6)

cnt <- 1
for(i in 1:3){
	for(j in (i+1):4){
		segments3d(X[c(i,j),])
		tmp <- X[i,] * r2[cnt] + X[j,] * (1-r2[cnt])
		spheres3d(tmp,color=3,radius=0.1)
		cnt <- cnt+1
	}
}

O <- X[1,]
A <- X[2,]
B <- X[3,]
C <- X[4,]
D <- r2[1] * X[1,] + (1-r2[1]) * X[2,]
E <- r2[4] * X[2,] + (1-r2[4]) * X[3,]
F <- r2[6] * X[3,] + (1-r2[6]) * X[4,]
G <- r2[3] * X[1,] + (1-r2[3]) * X[4,]
H <- r2[2] * X[1,] + (1-r2[2]) * X[3,]
I <- r2[5] * X[2,] + (1-r2[5]) * X[4,]
plot3d(X.,)
for(i in 1:3){
	for(j in (i+1):4){
		segments3d(X[c(i,j),])
		tmp <- X[i,] * r2[cnt] + X[j,] * (1-r2[cnt])
	}
}
spheres3d(X,radius=0.1)
spheres3d(D,radius=0.1,col=4)
spheres3d(G,radius=0.1,col=4)
spheres3d(E,radius=0.1,col=5)
spheres3d(F,radius=0.1,col=5)
spheres3d(H,radius=0.1,col=4)
spheres3d(I,radius=0.1,col=4)

simplex <- function(n) {
	qr.Q(qr(matrix(1,nrow=n)),complete=T)[,-1]
}
X <- simplex(4)
r2 <- rep(1/2,6)

cnt <- 1
for(i in 1:3){
	for(j in (i+1):4){
		segments3d(X[c(i,j),])
		tmp <- X[i,] * r2[cnt] + X[j,] * (1-r2[cnt])
		spheres3d(tmp,color=3,radius=0.1)
		cnt <- cnt+1
	}
}

O <- X[1,]
A <- X[2,]
B <- X[3,]
C <- X[4,]
D <- r2[1] * X[1,] + (1-r2[1]) * X[2,]
E <- r2[4] * X[2,] + (1-r2[4]) * X[3,]
F <- r2[6] * X[3,] + (1-r2[6]) * X[4,]
G <- r2[3] * X[1,] + (1-r2[3]) * X[4,]
H <- r2[2] * X[1,] + (1-r2[2]) * X[3,]
I <- r2[5] * X[2,] + (1-r2[5]) * X[4,]
plot3d(X.,)
for(i in 1:3){
	for(j in (i+1):4){
		segments3d(X[c(i,j),])
		tmp <- X[i,] * r2[cnt] + X[j,] * (1-r2[cnt])
	}
}
spheres3d(X,radius=0.1)
spheres3d(D,radius=0.1,col=4)
spheres3d(G,radius=0.1,col=4)
spheres3d(E,radius=0.1,col=5)
spheres3d(F,radius=0.1,col=5)
spheres3d(H,radius=0.1,col=4)
spheres3d(I,radius=0.1,col=4)
  • （３）整数、三角関数、チョッキリなこと
    • ひたすら調べる

# [3]

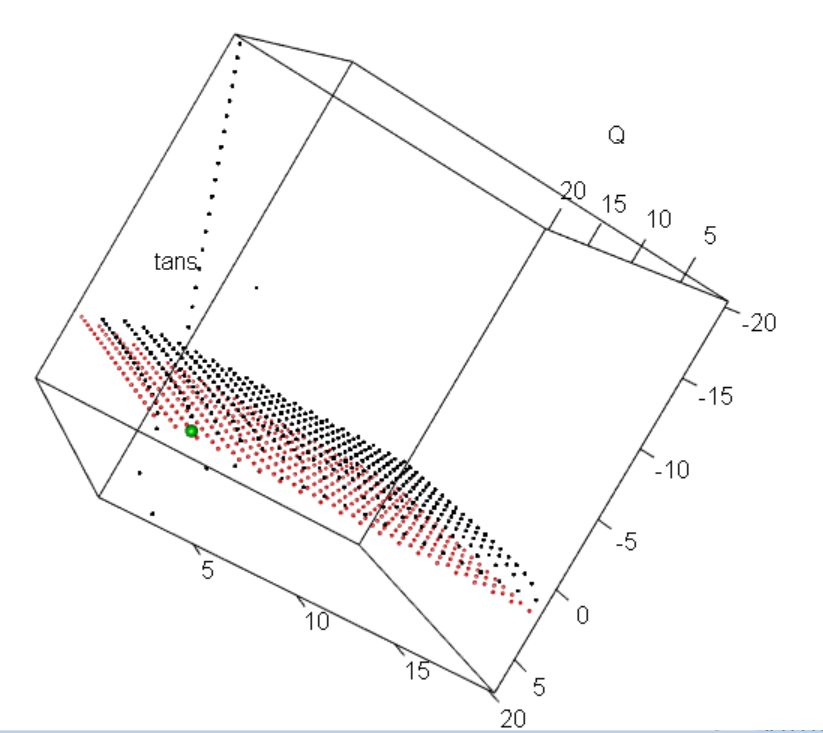
p <- q <- 1:20
pq <- as.matrix(expand.grid(p,q))
P <- pq[,1]
Q <- pq[,2]
alpha <- atan(1/P)
beta <- atan(1/Q)
tans <- tan(alpha+2*beta)

plot3d(P,Q,tans)
spheres3d(P,Q,2,col=2,radius=0.1)

pq[which(abs(tans-2)<10^(-12)),]
  • （４）円、三角形、三角関数
    • 外接円を原点中心単位円とし、Aを(1,0)に固定して、BをAから外接円周上、半周させる。それに合わせてCを決める
    • 円の面積を用いて内接円半径を求め、Aから角Aの二等分線上にしかるべき距離の点として内接円中心を描く


# [4]

## 外接円は原点中心の単位円
## A = (1,0)

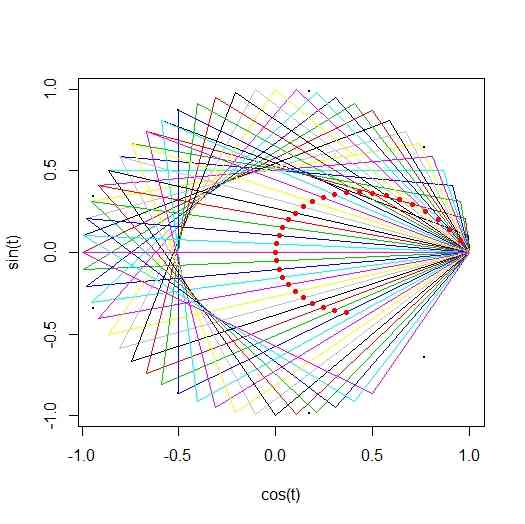
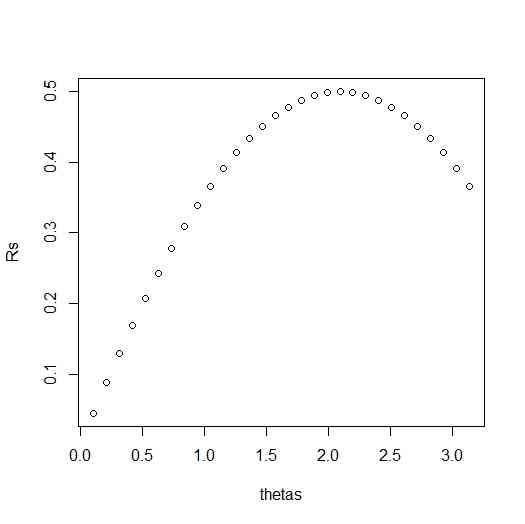
A <- c(1,0)
thetas <- seq(from=0,to=pi,length=31)
thetas <- thetas[-1]
Bs <- cbind(cos(thetas),sin(thetas))

Cs <- matrix(0,length(thetas),2)
Rs <- rep(0,length(thetas))
InCtr <- matrix(0,length(thetas),2)
for(i in 1:length(thetas)){
	v.B <- Bs[i,]-A
	v.B <- v.B/sqrt(sum(v.B^2)) # 単位ベクトル
	tmp.phi <- Arg(v.B[1]+1i*v.B[2])
	tmp.phi2 <- tmp.phi + pi/3
	r <- -2*cos(tmp.phi2)
	Cs[i,] <- c(r * cos(tmp.phi2) + 1,r*sin(tmp.phi2))
	
	# 内接円半径
	## 三角形面積
	lenAB <- sqrt(sum((Bs[i,]-A)^2))
	lenAC <- sqrt(sum((Cs[i,]-A)^2))
	lenBC <- sqrt(sum((Bs[i,]-Cs[i,])^2))
	area2 <- lenAB * lenAC * sin(pi/3)
	Rs[i] <- area2/(lenAB+lenAC+lenBC)
	tmp.phi3 <- tmp.phi + pi/6
	InCtr[i,] <- A + (Rs[i]/sin(pi/6)) * c(cos(tmp.phi3),sin(tmp.phi3))
	
}

t <- seq(from=0,to=2*pi,length=10)

plot(cos(t),sin(t),pch=20,cex=0.1)

for(i in 1:length(thetas)){
	segments(A[1],A[2],Bs[i,1],Bs[i,2],col=i)
	segments(Bs[i,1],Bs[i,2],Cs[i,1],Cs[i,2],col=i)
	segments(A[1],A[2],Cs[i,1],Cs[i,2],col=i)
}

points(InCtr,col=2,pch=20)

plot(thetas,Rs)
  • （５）微分積分
    • 特定の範囲にひかれた曲線とそれをよぎる直線とに挟まれる領域の面積が直線の傾きによって変化する。面積を最小にする直線は？



# 5
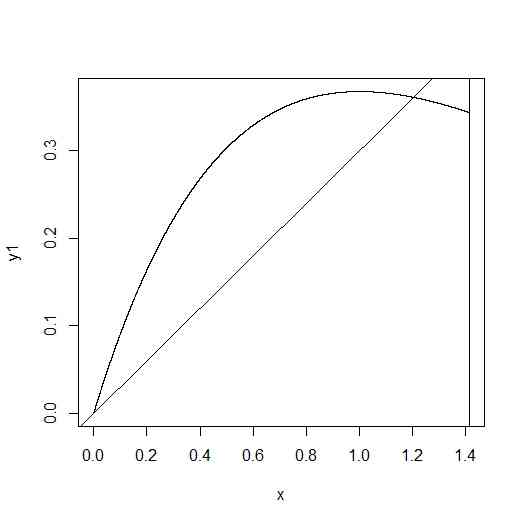
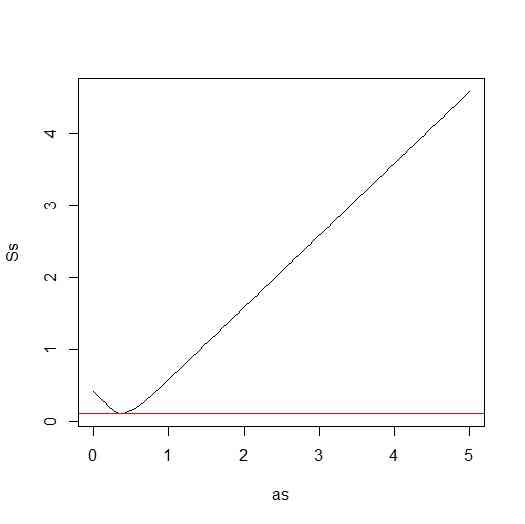
x <- seq(from=0,to=sqrt(2),length=10000)
a <- 0.3
y1 <- x * exp(-x)
y2 <- a * x

plot(x,y1,type="l")
abline(0,a)
abline(v=sqrt(2))


diff.y <- y1-y2
s <- sum(abs(diff.y) * (x[2]-x[1]))

# aを変えてみる
as <- seq(from=0,to=5,length=100)
Ss <- rep(0,length(as))
for(i in 1:length(as)){
	a <- as[i]
	y2 <- a * x
	diff.y <- y1-y2
	Ss[i] <- sum(abs(diff.y) * (x[2]-x[1]))
}

plot(as,Ss,type="l")
abline(h=min(Ss),col=2)


min.a <- as[which(Ss==min(Ss))]
a <- min.a
y1 <- x * exp(-x)
y2 <- a * x

plot(x,y1,type="l")
abline(0,a)
abline(v=sqrt(2))
  • （６）1,2,3,4,5でできたn桁の自然数が3で割り切れる確率
    • ランダム発生させてみる


# まずはべたにやってみる
# [6]

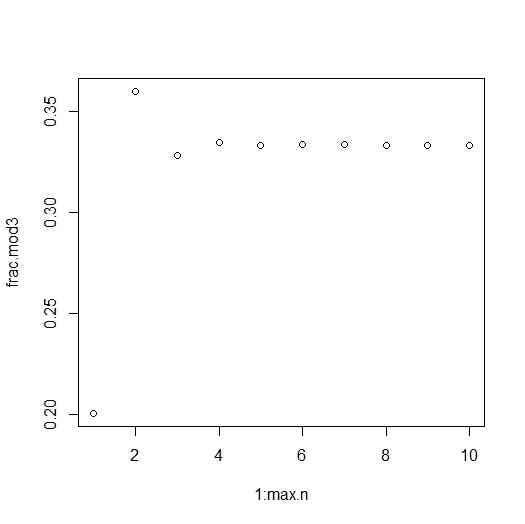
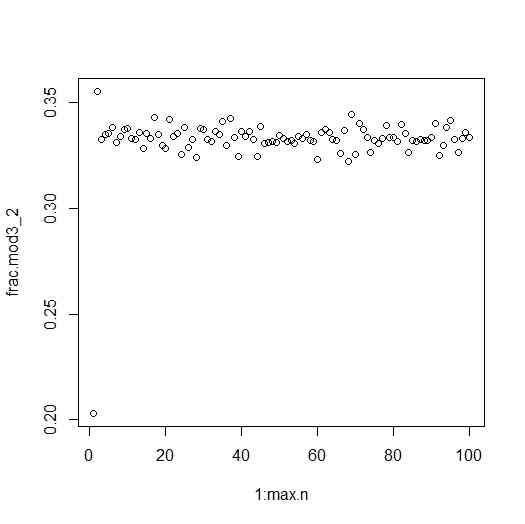
rep.num <- 10^6

max.n <- 10

r <- matrix(sample(1:5,max.n*rep.num,replace=TRUE),ncol=max.n)

frac.mod3 <- rep(0,max.n)
frac.mod3[1] <- length(which(r[,1] %% 3==0))/rep.num

frac.mod3_2 <- frac.mod3
for(i in 2:max.n){
	r10 <- r[,1:i] %*% 10^(0:(i-1))
	tmp <- r10 %% 3
	frac.mod3[i] <- length(which(tmp==0))/rep.num
	tmp.sum <- apply(r[,1:i],1,sum) # これでも同じ
	frac.mod3_2[i] <- length(which(tmp.sum%%3==0))/rep.num 
}


plot(1:max.n,frac.mod3)

plot(frac.mod3,frac.mod3_2)
frac.mod3-frac.mod3_2
# 各桁の値の和の割り切れるかどうかを調べてもよいことを確認

# 桁の値の和の計算の方が楽なので、それを使って桁数を増やしてやってみる
# 桁数を増やすことで、各桁での試行回数を減らしても、挙動の情報は取れるので、そのようにして見る
max.n <- 100
rep.num <- 10^4
r <- matrix(sample(1:5,max.n*rep.num,replace=TRUE),ncol=max.n)

frac.mod3 <- rep(0,max.n)
frac.mod3[1] <- length(which(r[,1] %% 3==0))/rep.num

frac.mod3_2 <- frac.mod3
for(i in 2:max.n){
	# 大変な計算をはしょる
	#r10 <- r[,1:i] %*% 10^(0:(i-1))
	#tmp <- r10 %% 3
	#frac.mod3[i] <- length(which(tmp==0))/rep.num
	tmp.sum <- apply(r[,1:i],1,sum) # これでも同じ
	frac.mod3_2[i] <- length(which(tmp.sum%%3==0))/rep.num 
}

plot(1:max.n,frac.mod3_2)