遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

共形変換でオタマジャクシ発生風

射影幾何 共形変換 複素解析 発生 多様体 曲面
  • 共形変換というのがある
  • 複素関数の分数を使って座標変換する
  • 「円」が｢円」に移される変換
  • こちらに色々な複素関数の変換がある
  • f(z) = k z^2とかf(z)=k z^{-2}とかだと、円にくびれを入れることができる
  • それは発生における脊索形成とかに擬せられる
  • こちらでやった、渦とpivot transformationよりシンプル(pivot transformationが共形変換の言葉で表現できる可能性はあるが…)
  • やってみる
  • まず、４次元空間の指数関数的増大円筒が卵に射影されることをやったが、その卵の長軸について、円をくびれさせる共形変換の原点を変化させて作ったのが以下

library(rgl)
f1 <- function(X){
	z <- X[,1] + 1i * X[,2]
	return(1/z)
}

f2 <- function(X,a){
	b <- Re(a) - 1i * Im(a)
	z <- X[,1] + 1i * X[,2]
	return((z-a)/(1-z*b))
}
f3 <- function(X){
	b <- Re(a) - 1i * Im(a)
	z <- X[,1] + 1i * X[,2]
	return(1/2*z^2)
}

# A parameter to decide number of visible windings
q <- 1
# kurtosis parameter
d <- 0.9
# A parameter of fatness
k <- 0.6
# Projection: x4 has component of x3
p <- 0

# conformal transform axis (x1,x2)座標により(x3,x4)の中心が決まる
# Q %*% t(c(x1,x2)) + c(X1,X2)
Q <- diag(rep(1,2))*10^(-4)
#as <- as/sqrt(sum(as^2))
# shift
shift <- c(0,0)
lambdas <- c(d,-1,0+q*1i,0-q*1i )
# A matrix to consist rotations in (x3,x4)-plane
V <- matrix(c(1,0,0,0,0,1,0,0,0,0,1,-1i*1,0,0,1,1i*1),4,4)
# A projection matrix: Two convergence points are specified at (1,0,0) and (-1,0,0)
M <- matrix(c(1,-1,0,0,0,0,1,0,0,0,0,1,1,1,p,0),byrow=TRUE,4,4)


x.init <- rep(1,4)
x.init[3:4] <- x.init[3:4]*k
t <- seq(from=-30,to=30,length=500)

X <- matrix(0,length(t),4)
for(i in 1:4){
	X[,i] <- x.init[i] * exp(lambdas[i]*t)
}

X. <- Re(t(V%*% t(X)))

# A surface is consisted of mulitple spirals that are made by rotation of the standard spiral in the original 4-dimensional space

phis <- seq(from=0,to=1,length=100)*2*pi
Y.all <- matrix(0,0,3)
for(ii in 1:length(phis)){
	Rot <- matrix(c(cos(phis[ii]),sin(phis[ii]),-sin(phis[ii]),cos(phis[ii])),2,2)
	X.2 <- X.
	X.2[,3:4] <- t(Rot %*% t(X.2[,3:4]))
	
	#for(iii in 1:length(X.2[,1])){
	#	ctr <- Q %*% X.2[iii,1:2] + shift
	#	tmp.v <- X.2[iii,3:4] -ctr

	#	tmp.v2 <- f3(matrix(tmp.v,nrow=1))
	#	tmp.v3 <- c(Re(tmp.v2),Im(tmp.v2))
	#	X.2[iii,3:4] <- tmp.v3 + ctr
	#}
	X.. <- t(M %*% t(X.2))
	Y <- X..[,1:3]/X..[,4]
	Y.all <- rbind(Y.all,Y)
}
Y.all.emb <- Y.all
qs <- seq(from=0.6,to=1,by=0.1)
q2s <- seq(from=0.3,to=1.1,by=0.2)
embs <- list()
cnt <- 1
for(i in 1:length(qs)){
	for(j in 1:length(q2s)){
		q <- qs[i]
		q2 <- q2s[j]
		tmp.emb <- Y.all
		for(ii in 1:length(Y.all[,1])){
			ctr <- q*Y.all.emb[ii,1] + q2
			tmp.v <- Y.all.emb[ii,2:3]
			tmp.v2 <- f3(matrix(tmp.v-c(ctr,0),nrow=1))
			tmp.v3 <- c(Re(tmp.v2),Im(tmp.v2))
			tmp.emb[ii,2:3] <- tmp.v3 +c(ctr,0)
		}
		tmp.emb[,1] <- tmp.emb[,1]+i*2
		tmp.emb[,3] <- tmp.emb[,3]+j*2
		embs[[cnt]] <- tmp.emb
		plot3d(my3Dstandard(embs[[cnt]]),type="l")
		cnt <- cnt + 1
	}
}
my3Dstandard <- function(x){
	rbind(x,rep(min(x),length(x[1,])),rep(max(x),length(x[1,])))
}
EMB <- matrix(0,0,3)
for(i in 1:length(embs)){
	current.emb <- embs[[i]]
	#if(i>1){
	#	current.emb[,1] <- current.emb[,1] + i
	#	current.emb[,3] <- current.emb[,3] + max(EMB[,3])
	#}
	
	plot3d(my3Dstandard(embs[[i]]),type="l")
	EMB <- rbind(EMB,current.emb)
}
#EMB. <- EMB
#EMB. <- rbind(EMB.,rep(min(EMB),3))
#EMB. <- rbind(EMB.,rep(max(EMB),3))

plot3d(my3Dstandard(EMB),type="l")


q <- 0.3
q2 <- 0.4
for(i in 1:length(Y.all[,1])){
	ctr <- q*Y.all.emb[i,1] + q2
	tmp.v <- Y.all.emb[i,2:3]
	tmp.v2 <- f3(matrix(tmp.v-c(ctr,0),nrow=1))
	tmp.v3 <- c(Re(tmp.v2),Im(tmp.v2))
	Y.all.emb[i,2:3] <- tmp.v3 +c(ctr,0)
}
col <- rep(1,length(Y.all[,1]))
minY <- min(Y.all)
maxY <- max(Y.all)
plot3d(rbind(Y.all,rbind(rep(minY,3),rep(maxY,3))),col=c(col,rep(2,2)),type="l")
Y.all.emb. <- Y.all.emb
Y.all.emb. <- rbind(Y.all.emb,rep(min(Y.all.emb),3))
Y.all.emb. <- rbind(Y.all.emb,rep(max(Y.all.emb),3))
plot3d(Y.all.emb.,type="l")
  • 共形変換は変換のための複素関数を与えて行う

x <- y <- seq(from=-1,to=1,length=100)
xy <- expand.grid(x,y)
R <- sqrt(apply(xy^2,1,sum))
col <- round(R*5)+1
f1 <- function(X){
	z <- X[,1] + 1i * X[,2]
	return(1/z)
}

out.f1 <- f1(xy)
par(mfcol=c(1,2))
plot(xy,col=col,pch=20)
plot(Re(out.f1),Im(out.f1),col=col,pch=20,xlim = c(-3,3),ylim=c(-3,3))
par(mfcol=c(1,1))

f2 <- function(X,a){
	b <- Re(a) - 1i * Im(a)
	z <- X[,1] + 1i * X[,2]
	return((z-a)/(1-z*b))
}
f3 <- function(X){
	b <- Re(a) - 1i * Im(a)
	z <- X[,1] + 1i * X[,2]
	return(1/2*z^2)
}
x <- y <- seq(from=-5,to=5,length=100)
xy <- as.matrix(expand.grid(x,y))

t <- seq(from=0,to=1,length=1000)*2*pi

ctr <- c(0.6,0.8)
rr <- seq(from=0.3,to=1.9,by=0.1)
X <- Y <- c()
for(i in 1:length(rr)){
	tmpX <- rr[i] * cos(t)+ctr[1]
	tmpY <- rr[i] * sin(t)+ctr[2]
	X <- c(X,tmpX)
	Y <- c(Y,tmpY)
}

#X <- 2 * cos(t) + 0.7
#Y <- 2 * sin(t) + 0.6
#X <- c(X,3.3*cos(t),0.9*cos(t))
#Y <- c(Y,3.3*sin(t),0.9*sin(t))
R <- sqrt(apply(xy^2,1,sum))
s <- which(R <= max(x)/sqrt(2))
xy <- xy[s,]
col <- floor(R[s]*5)+2
col <- c(col,rep(1,length(X)))
a <- -0.5 - 1i * 0.5
out.f2 <- f2(rbind(xy,cbind(X,Y)),a)
out.f3 <- f3(rbind(xy,cbind(X,Y)))
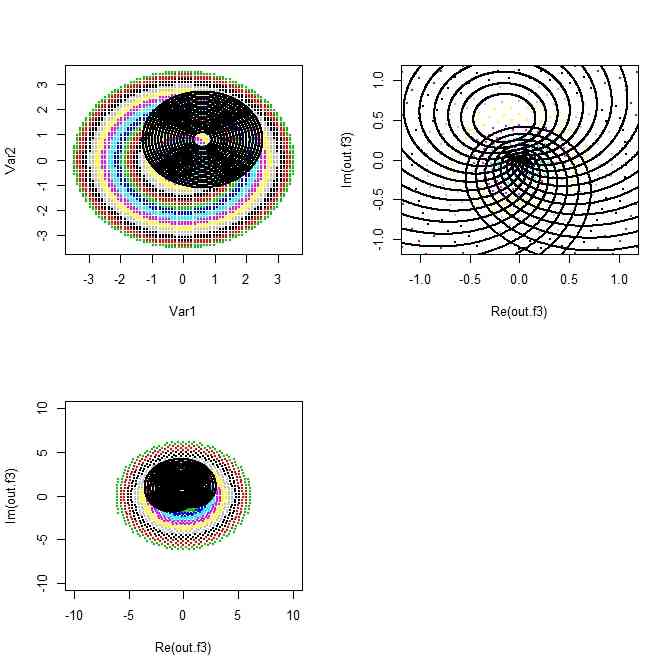
par(mfcol=c(2,2))
plot(rbind(xy,cbind(X,Y)),col=col,pch=20,cex=0.3)
plot(Re(out.f3),Im(out.f3),col=col,pch=20,xlim = c(-10,10),ylim=c(-10,10),cex=0.3)
plot(Re(out.f3),Im(out.f3),col=col,pch=20,xlim = c(-1.1,1.1),ylim=c(-1.1,1.1),cex=0.3)
#plot(Re(out.f3),Im(out.f3),col=col,pch=20,asp=TRUE,cex=0.3)
par(mfcol=c(1,1))