Windows 11で、ショートカットを使って添付メールを作る
- Windows10までは、とあるファイルを添付したメールを作成するには
- Windows11 になり、これができなくなった
- Window11の場合、添付したいファイルを右クリックすると、現れるメニューがWindows10時代から変わっており、「送る」がない
- その変わり、右クリック内オプションに「その他のオプションを表示」というのがある
- それを選ぶと、Windows10の右クリックメニューとほぼ同じメニューになる
- その中に「送る」はあるのだが、添付メールとして送る、というメニューがない
- 「送る=SendTo」にメーラーアプリを紐づけたりもしたが、うまくいかずに困っていた
- と、そんな折、添付したいファイルを右クリックし、メニューを開いたときに、「その他のオプションを表示」ではなく、「プログラムから開く」を選ぶと、そこにメーラーがあり、それを選ぶと、Windows10の「送る」「添付ファイルとして送る」と同じ動作がされることが解った
- めでたしめでたし
ぱらぱらめくる『線形代数と数え上げ』
- カステレイン行列と数え上げのことが気になった
- その両方が含まれている本書を買って眺めてみる
![線形代数と数え上げ[増補版] [ 高崎 金久 ] 線形代数と数え上げ[増補版] [ 高崎 金久 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/9616/9784535789616_1_3.jpg?_ex=128x128)
- 価格: 3190 円
- 楽天で詳細を見る
- この本の扱うトピックの英語版としては、Mishigan State Univ. がPDFをアップロードしていて(
[https://users.math.msu.edu/users/bsagan/Books/Aoc/final.pdf:title=Combinatorics:
The Art of Counting] by Bruce E. Sagan、その書籍版が
- 前書き
- 増補版まえがき
- 第1部 3次元ヤング図形の数え上げ
- 第1章 平面分割と非交差経路
- 第2章 LGV公式
- 第3章 平面分割とシューア函数
- 第4章 ヤコビ-トゥルーディ公式
- 第5章 非交差経路とフェルミオン
- 第6章 ワイルの指標公式
- 第7章 マクマホンの公式
- 第8章 平面分割の対角断面
- 第9章 平面分割と非交差経路
- 第2部 完全マッチングと全域木の数え上げ
- 第10章 ダイマー模型
- 第11章 カステレイン行列
- 第12章 有限正方格子上のダイマー模型
- 第13章 パフ式とその使い方
- 第12章 全域木の数え上げ
- 第13章 全域木と完全マッチングの対応
- 付録A
- 付録B
- 付録C 発展的話題
前書き
- 「行列と木の定理』
- カステレインの定理
- 非交差経路和に対するLGV(Lindstrom-Gessel-Viennot)公式
第1部 3次元ヤング図形の数え上げ
第1章 平面分割と非交差経路
- LGV公式が本書全体の中心
- LGV公式の行列式を計算する過程でシューア函数が登場する
- シューア函数は多変数対称多項式の古典的な例。表現論・可積分系・パンルヴェ方程式などとも関係が深い
- 3次元ヤング図形は、単位立方体を原点詰めで第一象限に積むパターンで、それは、行列の左上を原点と見た平面格子と考えたときに非負整数要素で大小制約のある行列として表現できる。この行列では、同じ整数を持った領域を区画と考えると、一種の平面分割になるので、3次元ヤング図形は平面分割を表しているとも見える
- これをさらに、非交差経路のセットとみることもできる
- LGV公式は、この非交差経路の場合の数にきれいな式表現(行列式を使う)を与える
- LGV公式が言っているのは
- これを使うと、正の整数 r,s,tでできた直方体と合致する3次元ヤング図形の場合の数の数え上げが
- さらに、シューア函数(対称性函数)を用いることで
と単純な式になる
my.macmahon <- function(r,s,t){ ret <- 1 for(i in 1:r){ for(j in 1:s){ for(k in 1:t){ ret <- ret * (i+j+k-1)/(i+j+k-2) } } } return(ret) } r <- 1 s <- 1 t <- 1 my.macmahon(r,s,t) # 1次元 rs <- 1:100 v <- rep(0,length(rs)) for(i in 1:length(rs)){ v[i] <- my.macmahon(rs[i],s,t) } plot(rs,v) # 2次元 n <- 9 rs <- 1:n ss <- n rss <- expand.grid(rs,ss) v <- rep(0,length(rss[,1])) for(i in 1:length(v)){ v[i] <- my.macmahon(rss[i,1],rss[i,2],t) } plot(rs,v)
第2章 LGV公式
第3章 平面分割とシューア函数
第4章 ヤコビ-トゥルーディ公式
第5章 非交差経路とフェルミオン
第6章 ワイルの指標公式
第7章 マクマホンの公式
- マクマホンの公式は整数の式。それを実数変数qで表された式で
の極限を取ったものとするという話
- 簡単な連続函数と、その極限として離散状態とを考え、数え上げとは極限(量子化)であるとの枠組み(か?)
- q-数え上げ ( q-enumeration ) と呼ばれる
- q-変形の例として、二項係数のq-form "q-binomial coefficient)を挙げる
- https://en.wikipedia.org/wiki/Gaussian_binomial_coefficient:titel=Wiki 英語記事に詳しい
と言う式が『線形代数と数え上げ』にあるが、この
は整数分割になっており、ちょっと面倒くさい
- Wiki記事の式によれば、
my.q.binom <- function(n,m,q){ ret <- 1 for(i in 1:m){ ret <- ret * (1-q^{n-i+1}) / (1-q^i) } return(ret) } q <- seq(from=-1,to=1.2,length=400) v <- rep(0,length(q)) n <- 5 m <- 2 V <- factorial(n)/(factorial(m)*factorial(n-m)) for(i in 1:length(v)){ v[i] <- my.q.binom(n,m,q[i]) } plot(q,v,type="l") abline(v=1) abline(h=V)

第8章 平面分割の対角断面
- シューア過程と呼ばれる確率過程の研究から注目を浴びるようになった
- 位相的弦理論に応用
第2部 完全マッチングと全域木の数え上げ
第10章 ダイマー模型
- ダイマー模型と2部グラフと完全マッチング
- タイリングとも関係
- ダイマー模型から、状態数、エネルギー状態などにつながり、量子力学的になる。全場合を網羅するのが「分配函数」。確率の総和が1になるようにする正規化項
- 「カステレインはダイマー模型の分配函数を線形代数的に計算する方法を示した」
- 「分配函数が直接に行列式として表せるのはグラフが平面的(な)場合に限られる」
- 平面化可能グラフは球面に描けるということ
- トーラスに描けるグラフについて拡張された
- 球面上の場合の分配函数は1個の行列
- トーラス上の場合の分配函数は4個の行列
- (球面に描ける)平面化可能グラフのダイマー模型のダイマーの取り方の場合の数(分配函数)は、カステレイン行列Kの行列式の絶対値
- カステレイン行列の要素は、N個の頂点セット2つを持つ2部グラフについてのNxN行列。行が第1セット、列が第2セットに対応し、第1・第2の頂点間にエッジがなければ0、エッジがあれば値が入る。その値は「そのダイマーの重みに符号をつけたもの」
- 「Kの固有ベクトルを直接構成して、Kを対格かし、その固有値の積としてKの行列式を表すことにしてみた
- 2m x 2n の正方格子の場合には
と美しい。。。
- さらに物理学的には、
において、自由エネルギーが
になるという
第11章 カステレイン行列
- 分配函数は、すべての場合の数
- 相関関数は、頂点重複のない辺の(亜)集合に対応する場合の数(ある周辺度数に対する場合の数に相当するだろう)
第12章 有限正方格子上のダイマー模型
- 扱いやすいグラフでやってみる
第13章 パフ式とその使い方
- パフ式は偶数次の反対称行列に定義される
- 外積代数と関係する
- 反対称行列だから箙と関係してくる
第12章 全域木の数え上げ
第13章 全域木と完全マッチングの対応
付録A
付録B
付録C 発展的話題
- トロピカル幾何・アメーバなどと絡んでくる:ダイマー模型とその周辺
グーグルマップの「所要時間」を得るための情報を分解する
- グーグルマップのルート検索・所要時間情報はかなり正確
- グーグルマップの利用者で位置情報を提供している人の情報をリアルタイムで収集し、その人が歩いているのか、車に乗っているのかなども判断したうえで、各道路の進み具合を計算し(それを色で表示し)、それらの積分値として所要時間を出すらしい
- 指定の日時での出発・到着に関する調べ物も可能で、その場合は(おそらく、過去の同一条件日(時刻や曜日)での情報を同様に集計して返してきているようだ。日時指定の場合は幅をもって所要時間が返ってくるので、情報を分布として収集してそのクオンタイルなどを出しているのだと思われる
- じゃあ、その検索を「自動化」するかもしれないとして、どうやったらできるかのための情報収集をしてみることにする
- 例えば、銀閣寺から金閣寺までの所要時間情報を取りたいとする
- グーグルクロームのGUIでその作業をやれば以下のようになる
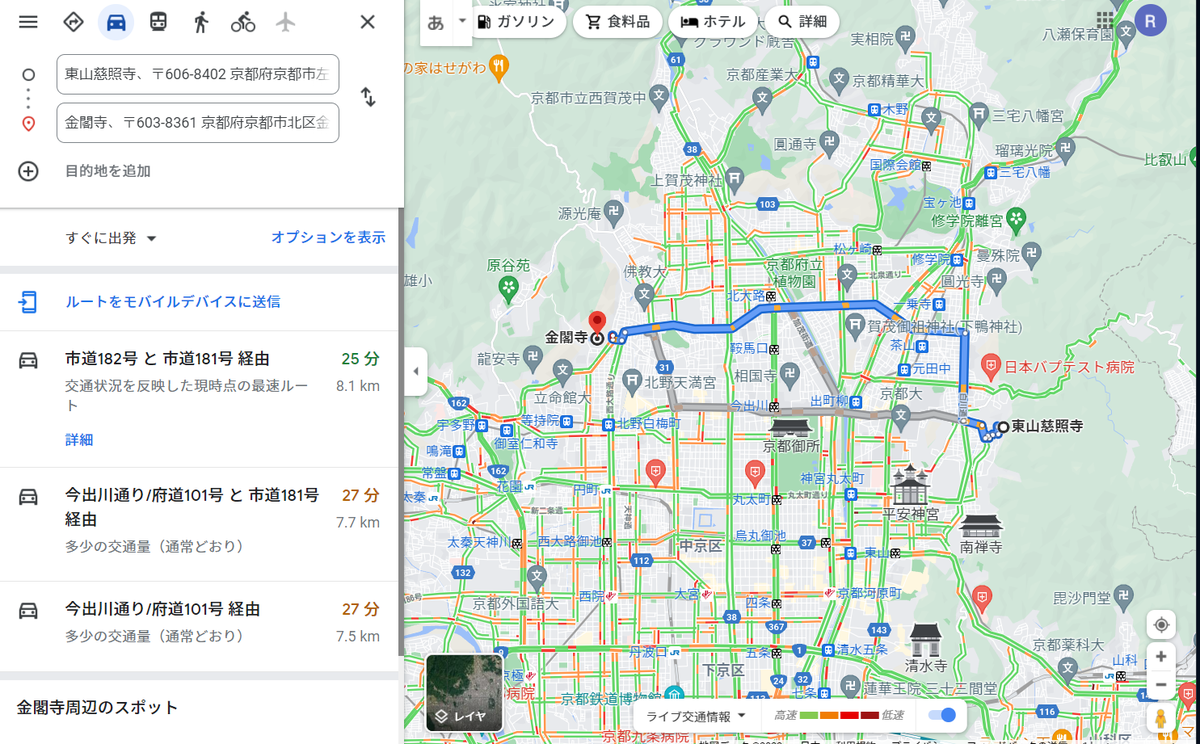
- このURLを引っ張り出してくると…
https://www.google.co.jp/maps/dir/%E6%9D%B1%E5%B1%B1%E6%85%88%E7%85%A7%E5%AF%BA%E3%80%81%E3%80%92606-8402+%E4%BA%AC%E9%83%BD%E5%BA%9C%E4%BA%AC%E9%83%BD%E5%B8%82%E5%B7%A6%E4%BA%AC%E5%8C%BA%E9%8A%80%E9%96%A3%E5%AF%BA%E7%94%BA%EF%BC%92/%E9%87%91%E9%96%A3%E5%AF%BA%E3%80%81%E3%80%92603-8361+%E4%BA%AC%E9%83%BD%E5%BA%9C%E4%BA%AC%E9%83%BD%E5%B8%82%E5%8C%97%E5%8C%BA%E9%87%91%E9%96%A3%E5%AF%BA%E7%94%BA%EF%BC%91/@35.0347898,135.728705,13z/data=!3m1!4b1!4m14!4m13!1m5!1m1!1s0x600109050b426fe1:0x258aca1ce888abc9!2m2!1d135.7982058!2d35.0270213!1m5!1m1!1s0x6001a820c0eb46bd:0xee4272b1c22645f!2m2!1d135.7292431!2d35.03937!3e0!5m1!1e1?hl=ja
- いかにも、エンコーディングで読めなくなっているっぽい部分が大量にある
- これらはあってもなくても多分大丈夫だろうと予想がつく
- 実際、この文字化けらしき部分を取り除いて、以下のようにしても、地図は得られる
https://www.google.co.jp/maps/dir//@35.0347898,135.728705,13z/data=!3m1!4b1!4m14!4m13!1m5!1m1!1s0x600109050b426fe1:0x258aca1ce888abc9!2m2!1d135.7982058!2d35.0270213!1m5!1m1!1s0x6001a820c0eb46bd:0xee4272b1c22645f!2m2!1d135.7292431!2d35.03937!3e0!5m1!1e1?hl=ja
- さて。余計な部分を削ったので、さらに調べることとする
- 大事なのは、「地点」を特定する情報で、それは緯度経度。その情報が
@35.0347898,135.728705,13z d135.7982058!2d35.0270213 d135.7292431!2d35.03937
- の当たりなのは、京都市の緯度が北緯35度くらいで経度が統計135度くらいであることを知っているから
- ちなみに、地図を表示して、経路を表示するために必要な位置特定情報は(1)地図の描画位置を決めるための情報と、(2)経路の始点情報と(3)経路の終点情報
- 上の3つの緯度・経度情報のうち、@で始まる方が描画位置のための情報で、残り2つが経路の始点終点のそれであることは、始点終点の緯度経度を調べればわかる
- ただし、この数字を変えただけでは、地図等の表示が変わらないので、何かしら数字ではないところの情報を使って全体として何かをコントロールしている模様だが、今はそこには興味がないので放っておく
- ちなみに
@35.0347898,135.728705,13z
- の 13z は表示時の拡縮パラメタになっており、数字が大きいほど狭い範囲をズームインして表示させる
- ルート検索のオプションで、出発時刻を「2022年1月1日午前9時」にしてやると、以下のように変わる
https://www.google.co.jp/maps/dir/''/''/@35.0345774,135.728705,13z/data=!3m1!4b1!4m18!4m17!1m5!1m1!1s0x600109050b426fe1:0x258aca1ce888abc9!2m2!1d135.7982058!2d35.0270213!1m5!1m1!1s0x6001a820c0eb46bd:0xee4272b1c22645f!2m2!1d135.7292431!2d35.03937!2m3!6e0!7e2!8j1641027600!3e0!5m1!1e1?hl=ja
- 丁寧に比べると
35.03937!3e0!5m1!1e1
- が
35.03937!2m3!6e0!7e2!8j1641027600!3e0!5m1!1e1
- に変わっていることがわかる
- 35.03937! は緯度情報で共通で、後半の !3e0!5m1!1e1 も共通である。違っているのは、次の文字列が挿入されていること
2m3!6e0!7e2!8j1641027600
- 今、出発時刻を1分、遅らせると
35.03937!2m3!6e0!7e2!8j1641027660!3e0!5m1!1e1
- となる。変わったのは
1641027600
- が
1641027660
- と、+60 されたこと。1分後倒しにして、+60されたということは、これは「60秒」のことと予想がつく
- 実際、60 x 60 x 24 = 86400 秒を足すと、24時間=1日後倒しになる。
- さて、今度は、出発時刻を指定する代わりに到着時刻を指定することにする。到着時刻を2022年1月1日の午前9時にすると
35.03937!2m3!6e1!7e2!8j1641027600!3e0!5m1!1e1
- となる。1641027600は元に戻り、代わりに次のような変化がある。0 --> 1である。これが「出発=0」「到着=1」
6e0
6e1
バドミントンのショートサーブ、どこをめがけて打つか
[https://journals.sagepub.com/doi/pdf/10.1177/1747954118812662:title=journals.sagepub.com
ro.ecu.edu.au
- シャトルコックは打ち出しの初期に速さの2乗に応じた減速加速度を受けて減速し、放物軌道に収束していくことが知られている
- ショートサーブでは
- ネットを越えること
- ネットを越えるが高すぎないこと
- サービスラインより奥に落ちること
- サービスラインに近い方が「よいサービス」とみなされることが多いが、実際には、サービスラインを越えさえすれば、レシーバは着地より相当前のタイミングでシャトルに触るので、「打ちにくさ」の方が、着地点自体より重要
- 「打ちにくさ」は、シャトルが上向きのときにレシーバが打てるかどうかと
- レシーバが触るときに、シャトルがネットより高い位置で触れるかどうかとで決まってくる
- レシーバがシャトルに触るのはネットを越えてからであるので、ネットを越えるタイミングで、それほど高い位置になく、かつ、すでに下向きの軌道に入っていると「打ちにくい」ことになる
- ネットを越えるタイミングで下向きであるということは、「シャトルの回転が収束し、シャトルの軸と進行方向が一致している」とするならば、重心軌道が下向きであることと同一であり、それは、軌道の最高到達点がサーバー側コート内にあることである
- このように「レシーバーが打ちにくい」=「良い」サービスの軌跡を、固定打ち出し点から描くために
- 打ち出し角度
- 打ち出し初速
- の2要因のみでコントロールするとして、どのような軌跡が可能かを考えてみる
- そして、「失敗の少ない、よいサービスの打ち方」とは、
- 打ち出し角度と打ち出し初速とに、ある程度の乱雑項が入ってしまっても、
- ネットにかかりにくく、
- ネット越えのときの高さが高くなりすぎず、
- サービスラインの手前に落ちにくく、
- 最高到達点がサーバー側にとどまりやすい
- ようなサービスを目標として打つ、ということと言える
- サービスを打つ時の「気持ちとしての目標」は
- 「ネットを越えるときの下向きベクトル」と「ネットを越えるときの高さ」にするのは難しいだろう(ネットの白帯の上、ぎりぎりを狙って打つ、というのは、白帯上に上向きベクトルを作ることを狙いがちになるので、うまくいかない)
- それよりは、ネットよりも自陣側のある地点のある高さを目標に、そこを通過するときに軌道が水平になるように狙うことの方が簡単そうだ
- Rでシミュレーションしてみる

m <- 5 * 10^(-3) g <- c(0,-9.8) st <- c(-200,115) * 10^(-2) net <- c(0,155) * 10^(-2) end <- c(198,0) * 10^(-2) rho <- 10^(-3.5) # best service #theta.init <- pi/5.5 #speed.init <- 6 dt <- 0.01 t <- seq(from=0,to=2,by=dt) my.short.service.sim <- function(theta.init,speed.init,m=5 * 10^(-3),g=c(0,-9.8),st=c(-200,115) * 10^(-2),net=c(0,155) * 10^(-2),end=c(198,0) * 10^(-2),rho=10^(-3.5),dt=0.01){ t <- seq(from=0,to=2,by=dt) cond <- expand.grid(theta.init,speed.init) n <- length(cond[,1]) ret <- list() for(i in 1:n){ #ret[[i]] <- 1:i this.theta <- cond[i,1] this.speed <- cond[i,2] vs <- matrix(0,length(t)+1,2) v.init <- this.speed * c(cos(this.theta),sin(this.theta)) vs[1,] <- v.init for(ii in 1:length(t)){ new.v <- vs[ii,] + dt * (g + rho * sqrt(sum(vs[ii,]^2)) * (-vs[ii,]) / m) vs[ii+1,] <- new.v } xs <- apply(vs*dt,2,cumsum) xs <- t(t(xs)+st) #print(xs) ret[[i]] <- matrix(0,length(t)+1,2) #print(ret[[i]]) ret[[i]] <- xs } #return(ret) return(list(ret=ret,cond=cond,t=t)) } theta.init <- seq(from=pi/7,to=pi/5,length=30) speed.init <- seq(from=5,to=8,length=30) out <- my.short.service.sim(theta.init,speed.init) plot(out$ret[[1]],type="l",ylim=c(0,2),asp=TRUE) abline(h=0) segments(0,0,net[1],net[2]) points(end[1],end[2],pch=20,col=2) for(i in 2:length(out$ret)){ points(out$ret[[i]],type="l",col=i) } too.high <- too.short <- peak.loc <- peak.hight <- rep(0,length(out$ret)) for(i in 1:length(too.high)){ this.xs <- out$ret[[i]] too.high[i] <- this.xs[which.min(this.xs[,1]^2)[1],2]-net[2] too.short[i] <- this.xs[which.min(this.xs[,2]^2)[1],1]-end[1] peak.loc[i] <- this.xs[which(this.xs[,2]==max(this.xs[,2]))[1],1] peak.hight[i] <- max(this.xs[,2])-net[2] } oks <- which(too.high > 0 & too.short > 0 & too.high < 0.1 & peak.loc < 0) oks.but.peakout <- which(too.high > 0 & too.short > 0 & too.high < 0.1 & peak.loc >= 0) ok.but.high <- which(too.high >= 0.1 & too.short > 0) ng.both <- which(too.high <= 0 & too.short <= 0) ng.high <- which(too.high <= 0 & too.short > 0) ng.short <- which(too.high > 0 & too.short <= 0) cond <- cbind(out$cond[,1]/pi,out$cond[,2]) par(mfcol=c(1,1)) plot(cond[,1],cond[,2],xlab="angle, pi",ylab="speed, m/s") points(cond[oks,],pch=20,col=2) points(cond[oks.but.peakout,],pch=15,col=6) points(cond[ng.both,],pch=20,col=1) points(cond[ng.high,],pch=20,col=3) points(cond[ng.short,],pch=20,col=4) points(cond[ok.but.high,],pch=20,col=5) # OKsの軌道だけを描く plot(out$ret[[oks[1]]],type="l",ylim=c(0,2),asp=TRUE) abline(h=0) segments(0,0,net[1],net[2]) points(end[1],end[2],pch=20,col=2) for(i in 2:length(oks)){ points(out$ret[[oks[i]]],type="l",col=i) } hsp <- cbind(too.short,too.high,peak.loc,peak.hight) pairs(hsp) par(mfcol=c(2,2)) plot(too.short,too.high,xla="floor short",ylab="oevrnet") abline(h=0,col=2) abline(v=0,col=3) plot(too.short,peak.loc,xla="floor short",ylab="peak.loc") abline(h=0,col=2) abline(v=0,col=3) plot(too.high,peak.loc,xla="overnet",ylab="peak.loc") abline(h=0,col=2) abline(v=0,col=3) plot(peak.loc,peak.hight,xla="peak.loc",ylab="peak.hight.overnet") abline(h=0,col=2) abline(v=0,col=3) for(i in 1:length(overnet)){ this.cond <- out$cond[i,] points(floor[i],overnet[i],pch=this.cond[1],col=this.cond[2]) }
- 条件を変えて、コートの後ろ半分から、アンダーハンドでレシーブをしつつ、奥へ飛ばさずに、ネットを越えたあたりに落としたい。その際、ショートサービスと同様に軌道の最高到達点を自陣側に持ってくるためには、どのくらいの角度と初速で飛ばせばよいのだろうか

m <- 5 * 10^(-3) g <- c(0,-9.8) st <- c(-450,30) * 10^(-2) net <- c(0,155) * 10^(-2) end <- c(198,0) * 10^(-2) rho <- 10^(-3.5) # best service #theta.init <- pi/5.5 #speed.init <- 6 dt <- 0.01 t <- seq(from=0,to=2,by=dt) my.short.service.sim <- function(theta.init,speed.init,m=5 * 10^(-3),g=c(0,-9.8),st=c(-200,115) * 10^(-2),net=c(0,155) * 10^(-2),end=c(198,0) * 10^(-2),rho=10^(-3.5),dt=0.01){ t <- seq(from=0,to=2,by=dt) cond <- expand.grid(theta.init,speed.init) n <- length(cond[,1]) ret <- list() for(i in 1:n){ #ret[[i]] <- 1:i this.theta <- cond[i,1] this.speed <- cond[i,2] vs <- matrix(0,length(t)+1,2) v.init <- this.speed * c(cos(this.theta),sin(this.theta)) vs[1,] <- v.init for(ii in 1:length(t)){ new.v <- vs[ii,] + dt * (g + rho * sqrt(sum(vs[ii,]^2)) * (-vs[ii,]) / m) vs[ii+1,] <- new.v } xs <- apply(vs*dt,2,cumsum) xs <- t(t(xs)+st) #print(xs) ret[[i]] <- matrix(0,length(t)+1,2) #print(ret[[i]]) ret[[i]] <- xs } #return(ret) return(list(ret=ret,cond=cond,t=t)) } theta.init <- seq(from=pi/5,to=pi/3,length=30) speed.init <- seq(from=9,to=10,length=2) out <- my.short.service.sim(theta.init,speed.init,st=st) plot(out$ret[[1]],type="l",ylim=c(0,6),asp=TRUE) abline(h=0) segments(0,0,net[1],net[2]) points(end[1],end[2],pch=20,col=2) for(i in 2:length(out$ret)){ points(out$ret[[i]],type="l",col=i) } too.high <- too.short <- peak.loc <- peak.hight <- rep(0,length(out$ret)) for(i in 1:length(too.high)){ this.xs <- out$ret[[i]] too.high[i] <- this.xs[which.min(this.xs[,1]^2)[1],2]-net[2] #too.short[i] <- this.xs[which.min(this.xs[,2]^2)[1],1]-end[1] too.short[i] <- this.xs[which.min(this.xs[,2]^2)[1],1] peak.loc[i] <- this.xs[which(this.xs[,2]==max(this.xs[,2]))[1],1] peak.hight[i] <- max(this.xs[,2])-net[2] } oks <- which(too.high > 0 & too.short > 0 & too.high < 0.1 & peak.loc < 0) oks.but.peakout <- which(too.high > 0 & too.short > 0 & too.high < 0.1 & peak.loc >= 0) ok.but.high <- which(too.high >= 0.1 & too.short > 0) ng.both <- which(too.high <= 0 & too.short <= 0) ng.high <- which(too.high <= 0 & too.short > 0) ng.short <- which(too.high > 0 & too.short <= 0) cond <- cbind(out$cond[,1]/pi,out$cond[,2]) par(mfcol=c(1,1)) plot(cond[,1],cond[,2],xlab="angle, pi",ylab="speed, m/s") points(cond[oks,],pch=20,col=2) points(cond[oks.but.peakout,],pch=15,col=6) points(cond[ng.both,],pch=20,col=1) points(cond[ng.high,],pch=20,col=3) points(cond[ng.short,],pch=20,col=4) points(cond[ok.but.high,],pch=20,col=5) # OKsの軌道だけを描く plot(out$ret[[oks[1]]],type="l",ylim=c(0,2),asp=TRUE) abline(h=0) segments(0,0,net[1],net[2]) points(end[1],end[2],pch=20,col=2) for(i in 2:length(oks)){ points(out$ret[[oks[i]]],type="l",col=i) }

![線形代数とネットワーク [ 高崎金久 ] 線形代数とネットワーク [ 高崎金久 ]](https://thumbnail.image.rakuten.co.jp/@0_mall/book/cabinet/8299/9784535788299.jpg?_ex=128x128)