2014-11-02

共形変換による２次元の形解析その２

共形変換形

昨日は共形変換によって形の異同をノルムに変える話だった
「形」〜「輪郭」だけだと、リーマンの写像定理から、「すべての輪郭は単位円に共形変換できる」ので、「共形変換」が作る距離空間(測度空間)で話をすることになるようだ
この場合には、「単位円」から「単位円」への共形変換もあるので、輪郭どうし、相互に対応する点、というのがどうにでも変えられる
ただ、我々が「視覚的」に形を見るときには、「シルエット」を見つつ、その内部に構造を感じながら、「輪郭＋内部構造」として比べていることが多いように思う。これが錯視の原因だったりもするのかと思うけれども
それはどういうことか、というと「輪郭」と「内部の点」での対応関係をとるので、「単位円」から「単位円」への共形変換は使えない、ということなのだろうと思う
では、その内部点は何個あれば、共形変換を「一意化」できるのだろうか(もし一意化できるとして、ですが)
ゆっくり共形変換を見ていく
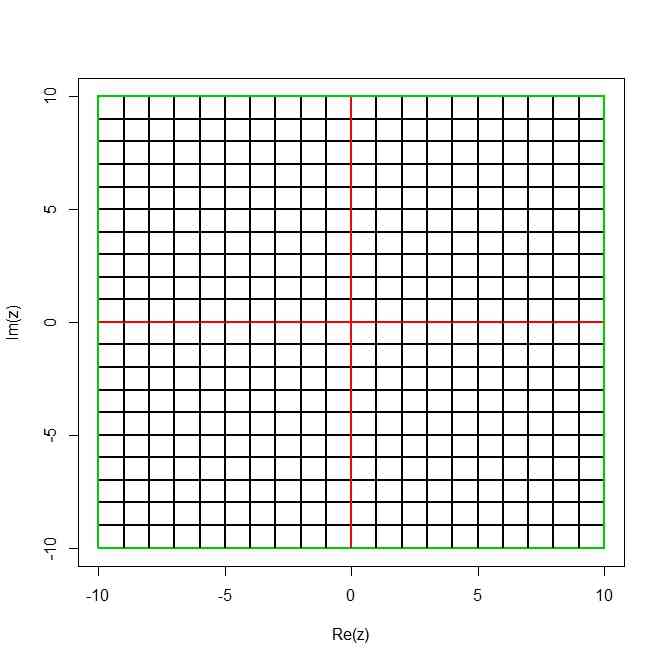
グリッドを描く。実軸と虚軸を赤。正方形の外周を緑

my.grid <- function(X=(-10):10,Y=(-10):10,n=200){
	x=seq(from=min(X),to=max(X),length=n+1)[-1]
	y=seq(from=min(Y),to=max(Y),length=n+1)[-1]
	as.matrix(rbind(expand.grid(x,Y),expand.grid(X,y)))
}
xy <- my.grid(X=(-10):10,Y=(-10):10,n=1000)
z <- xy[,1] + 1i * xy[,2]
col <- rep(1,length(z))
col[which(Re(z)==0)] <- 2
col[which(Im(z)==0)] <- 2
col[which(abs(Re(z))==abs(max(Re(z))))] <- 3
col[which(abs(Im(z))==abs(max(Im(z))))] <- 3
plot(z,pch=20,cex=0.5,col=col)

基本はだが、このは回転と拡大、は平行移動
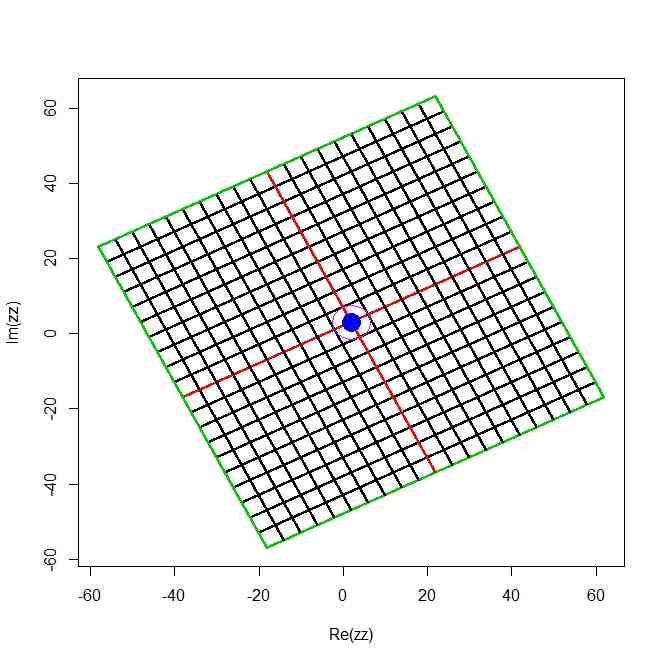
- 青い大きなドットが平行移動分(bの座標)
- 回転しているが、グリッドの１単位がMod(a)であることが紫の円で示してある

a <- 4+1i*2
b <- 2+1i*3
zz <- a*z+b
t <- seq(from=0,to=1,length=100)*2*pi
xx <- cos(t)*Mod(a)
yy <- sin(t)*Mod(a)
plot(zz,pch=20,cex=0.5,col=col)
points(b,col=4,pch=20,cex=4)
points(b+xx + 1i*yy,col=6,type="l")

$z^k$ でどう変わるかを見てみる

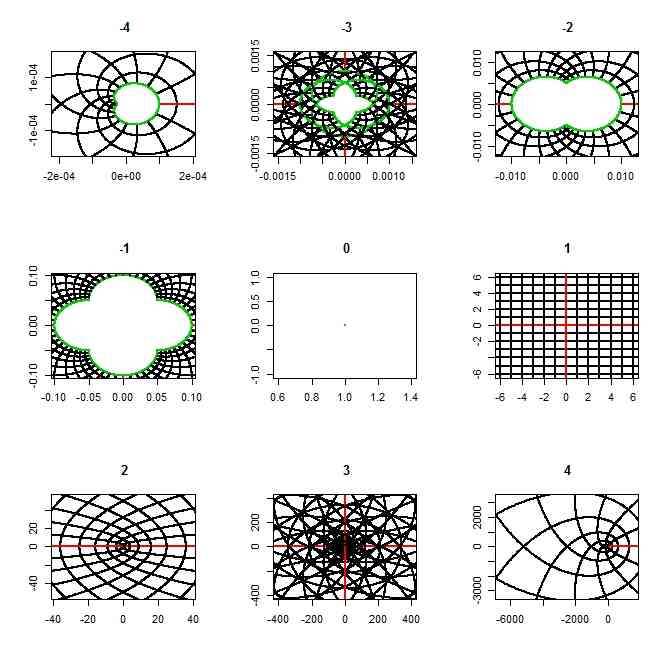
- k < 0 では中央付近に空白があって、緑の線で囲まれる。これはk < 0のときには、原点が無限遠に、無限遠が0に移るから
- k = 0 では、すべてが1 + 0i
- k > 0 で言うとk=1,2,4は「きれいな形」。これは、z^kでは、角度がk倍されるわけなので、偶数倍だと、うまくつじつまが合うから(一つのグリッド線に複数の線が対応している)

n.beki <- 9
bekis <- 1:n.beki
bekis <- seq(from=-4,to=4,length=9)
my.f.beki <- function(z,b)z^b
par(mfrow=c(3,3))
for(i in 1:length(bekis)){
	tmp <- my.f.beki(z,begis[i])
	xlim <- quantile(Re(tmp),c(0.2,0.8))
	ylim <- quantile(Im(tmp),c(0.2,0.8))
	plot(tmp,pch=20,cex=0.1,xlab="",ylab="",main=paste("",bekis[i]),xlim=xlim,ylim=ylim,col=col)
}

par(mfcol=c(1,1))

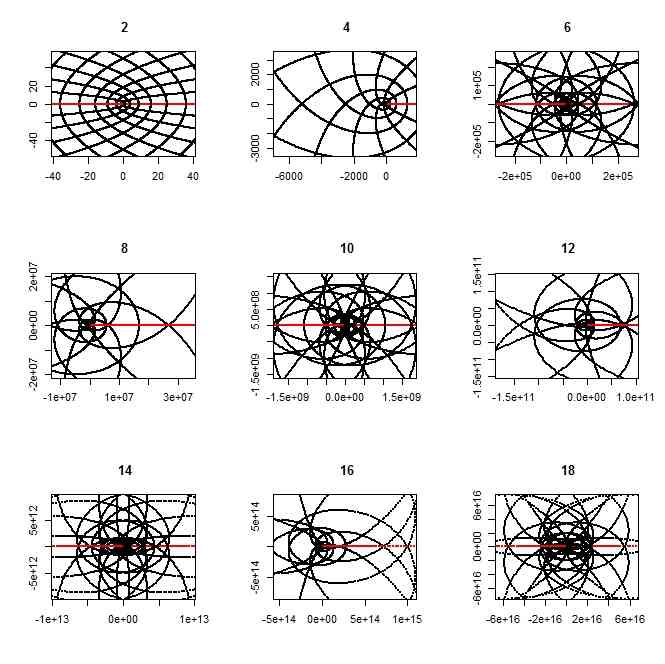
kが４の倍数のときは、実軸と虚軸の両方が実軸の非負に集結し、kが偶数だけれど４の倍数でないときには、虚実の軸が実軸全体に集結していることが次の図でわかる
この「重なる」というのは、 $\sum_{i=0}^n a_i z^i=f(z)=z$ という不動点について考えたとき、n個の点が不動点である。たとえば、 $f(z)=az+b=z$ とすると、不動点は $z=\frac{b}{a-1}$ 、 $f(z)=z^2=z$ の不動点は $z(z-1)=0$ の２点、 $f(z)=z^4=z$ の不動点は $z(z^3-1)=0$

bekis <- 1:n.beki
bekis <- seq(from=1,to=9,length=9)*2

par(mfrow=c(3,3))
for(i in 1:length(bekis)){
	tmp <- my.f.beki(z,bekis[i])
	xlim <- quantile(Re(tmp),c(0.2,0.8))
	ylim <- quantile(Im(tmp),c(0.2,0.8))
	plot(tmp,pch=20,cex=0.1,xlab="",ylab="",main=paste("",bekis[i]),xlim=xlim,ylim=ylim,col=col)
}

par(mfcol=c(1,1))

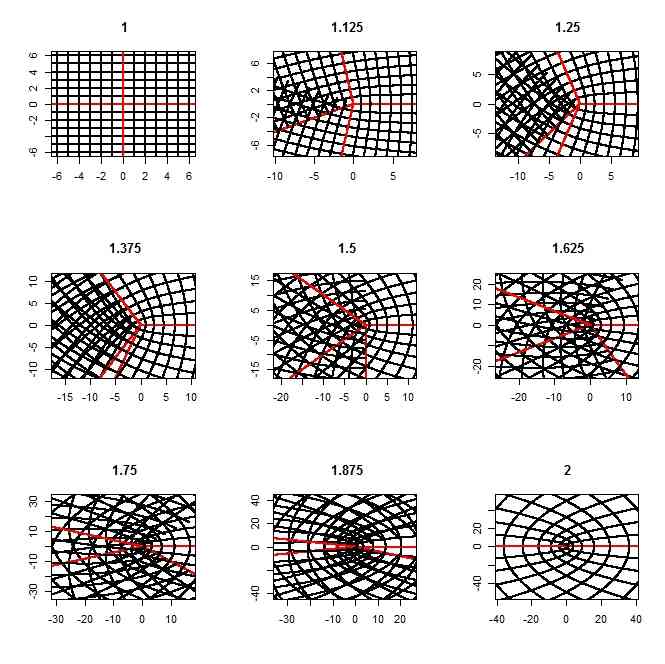
kが偶数でないときは、ピタリと重ならないので、ずれが生じるわけだけれど、その様子を1-2の間で試してみると、その「重ならない様子」が見て取れる

bekis <- 1:n.beki
bekis <- seq(from=1,to=2,length=9)


par(mfrow=c(3,3))
for(i in 1:length(bekis)){
	tmp <- my.f.beki(z,bekis[i])
	xlim <- quantile(Re(tmp),c(0.2,0.8))
	ylim <- quantile(Im(tmp),c(0.2,0.8))
	plot(tmp,pch=20,cex=0.1,xlab="",ylab="",main=paste("",bekis[i]),xlim=xlim,ylim=ylim,col=col)
}

par(mfcol=c(1,1))

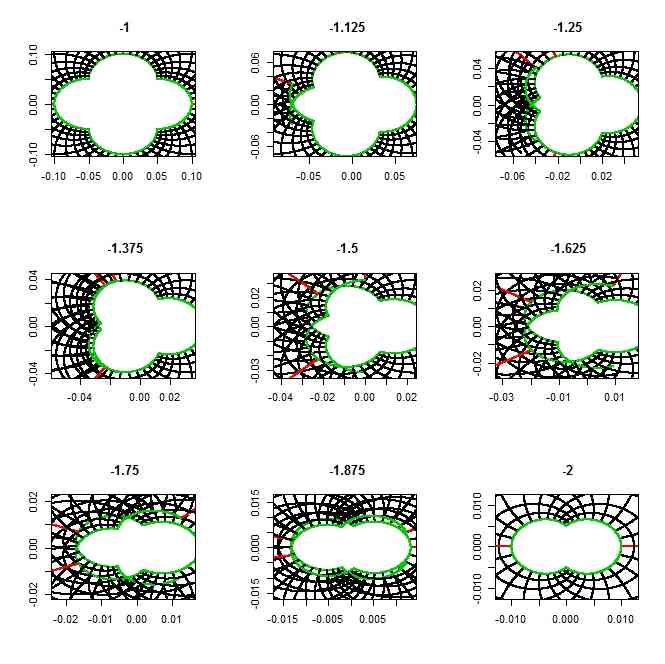
k<0の範囲でも「ピタリと重なる」場合と、そうでない場合とが、同様にある

bekis <- 1:n.beki
bekis <- seq(from=1,to=2,length=9)*(-1)

par(mfrow=c(3,3))
for(i in 1:length(bekis)){
	tmp <- my.f.beki(z,bekis[i])
	xlim <- quantile(Re(tmp),c(0.2,0.8))
	ylim <- quantile(Im(tmp),c(0.2,0.8))
	plot(tmp,pch=20,cex=0.1,xlab="",ylab="",main=paste("",bekis[i]),xlim=xlim,ylim=ylim,col=col)
}

par(mfcol=c(1,1))

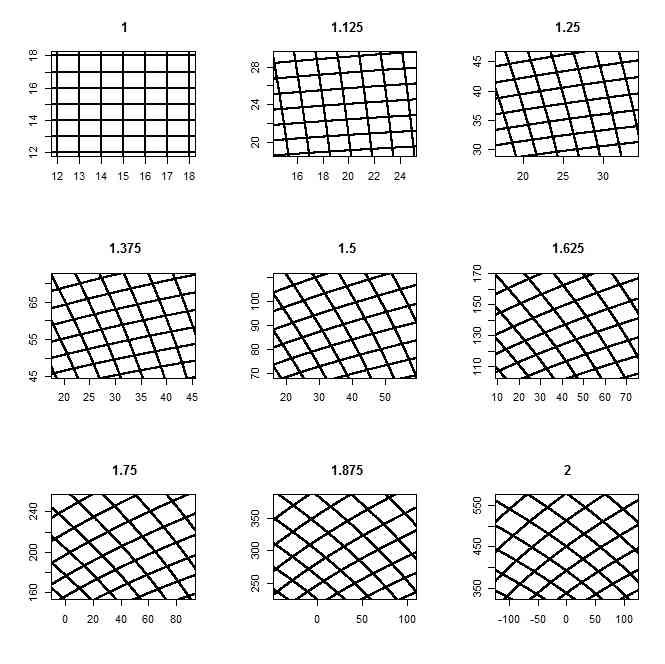
たしかに、この「ぐるりん」と回って重なる、とか、それが「ぴたりと重なる」とかは、美しいのだけれど、「正の数の世界」では、そのあたりは、あまり存在していないのではないか、とも思えます。そんな重なりが生じない領域だけを拡大してみてみると、ねじれの具合の強弱という違いとして見て取れる

xy <- my.grid(X=10:20,Y=10:20,n=1000)
z <- xy[,1] + 1i * xy[,2]
col <- rep(1,length(z))
col[which(Re(z)==0)] <- 2
col[which(Im(z)==0)] <- 2
col[which(abs(Re(z))==abs(max(Re(z))))] <- 3
col[which(abs(Im(z))==abs(max(Im(z))))] <- 3
bekis <- 1:n.beki
bekis <- seq(from=1,to=2,length=9)

par(mfrow=c(3,3))
for(i in 1:length(bekis)){
	tmp <- my.f.beki(z,bekis[i])
	xlim <- quantile(Re(tmp),c(0.2,0.8))
	ylim <- quantile(Im(tmp),c(0.2,0.8))
	plot(tmp,pch=20,cex=0.1,xlab="",ylab="",main=paste("",bekis[i]),xlim=xlim,ylim=ylim,col=col)
}

par(mfcol=c(1,1))