遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

ぱらぱらめくる『曲面と多様体』2. 曲面論

多様体 曲線 曲面 ぱらぱらめくるシリーズ R
  • 2. 曲面論
    • パラメタ表示された曲面を描いてみよう
    • 曲面とは\mathbf{R}^3の部分集合で、局所的に２つのパラメタで表されるもの
    • ２つのパラメタの偏微分が１次独立であると「都合がよい」
    • 閉曲面は有界(含まれている範囲が有限)で、境界がない曲面
    • 裏と表。曲面が空間内である部分を囲んでいると、その曲面には囲んでいる空間側とそうでない側の区別(裏表)ができるが、メビウスの輪にはそれがない→単側曲面、向き付け不可能曲面
    • 向き付け不可能な閉曲面は存在しない
    • 自身と交差する曲面は、向き付け不可能な閉曲面とみることもできる→クラインの壺
      • 自己交差のところでは、同じ点に、2つまたはそれ以上の枚数の曲面が通過する。それぞれの曲面が「曲面の条件」を満たしていること

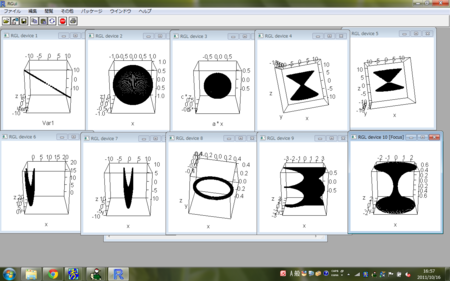
  • 曲面を２パラメタで表したとき、それぞれのパラメタで偏微分して接ベクトルが２つ得られる。これらが１次独立なとき、この２つの接ベクトルを基底とした線形部分空間が取れて、これが接平面(Rで、２パラメタ表現し、その式をderiv()関数で微分して、この様子を見てみる

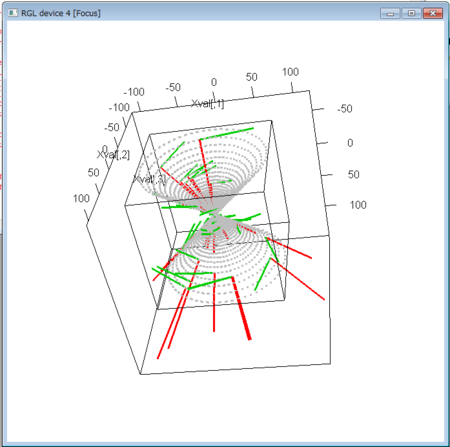
  • さらに、法線ベクトルは、２つの接ベクトルの外積ベクトルであるから、外積ベクトルの計算は、こちらの記事で書いたRの関数を使って、付加してみる

# 曲面
x<-y<-seq(from=-10,to=10,length=20)
xy<-expand.grid(x,y)
# 例2.1 平面
a<-runif(1)
b<-runif(1)
c<-runif(1)
d<-runif(1)
z<-(d-a*xy[,1]-b*xy[,2])/c
xyz<-cbind(xy,z)
plot3d(xyz)
#Z<-matrix(z,length(x),length(y))
#persp(Z,x=x,y=y)

# 例2.9 球面
u<-v<-seq(from=-1,to=1,length=100)*pi
uv<-expand.grid(u,v)
x<-cos(uv[,1])*cos(uv[,2])
y<-cos(uv[,1])*sin(uv[,2])
z<-sin(uv[,1])
open3d()

plot3d(x,y,z,type="l")

# 例2.10 楕円面

a<-runif(1)
b<-runif(1)
c<-runif(1)
xlim<-ylim<-zlim<-c(-max(a,b,c),max(a,b,c))
open3d()
plot3d(a*x,b*y,c*z,type="l",xlim=xlim,ylim=ylim,zlim=zlim)

# 例2.11 １葉双曲面
u<-v<-seq(from=-1,to=1,length=100)*pi
uv<-expand.grid(u,v)
x<-a*cosh(uv[,1])*cos(uv[,2])
y<-b*cosh(uv[,1])*sin(uv[,2])
z<-c*sinh(uv[,1])
open3d()
xlim<-ylim<-zlim<-range(c(x,y,z))

plot3d(x,y,z,xlim=xlim,ylim=ylim,zlim=zlim)

# 例2.12 ２葉双曲面
u<-v<-seq(from=-1,to=1,length=100)*pi
uv<-expand.grid(u,v)
x<-a*cosh(uv[,1])*cos(uv[,2])
y<-b*cosh(uv[,1])*sin(uv[,2])
z<-c*cosh(uv[,1])
z2<--c*z
open3d()
x<-c(x,x)
y<-c(y,y)
z<-c(z,z2)
xlim<-ylim<-zlim<-range(c(x,y,z))

plot3d(x,y,z,xlim=xlim,ylim=ylim,zlim=zlim)

# 例2.13 楕円放物面
x<-a*uv[,1]
y<-b*uv[,2]
z<-uv[,1]^2+uv[,2]^2

xlim<-ylim<-zlim<-range(c(x,y,z))

open3d()

plot3d(x,y,z,xlim=xlim,ylim=ylim,zlim=zlim)

# 例2.14 双曲放物面
x<-a*uv[,1]
y<-b*uv[,2]
z<-uv[,1]^2-uv[,2]^2

open3d()
xlim<-ylim<-zlim<-range(c(x,y,z))


plot3d(x,y,z,xlim=xlim,ylim=ylim,zlim=zlim)

# 例2.15 トーラス
R<-runif(1)
r<-runif(1)*R

x<-(R+r*cos(uv[,1]))*cos(uv[,2])
y<-(R+r*cos(uv[,1]))*sin(uv[,2])
z<-r*sin(uv[,1])
xlim<-ylim<-zlim<-range(c(x,y,z))

open3d()

plot3d(x,y,z,xlim=xlim,ylim=ylim,zlim=zlim)

# 例2.16 螺旋面
a<-runif(1)
x<-uv[,1]*cos(uv[,2])
y<-uv[,1]*sin(uv[,2])
z<-a*uv[,2]
xlim<-ylim<-zlim<-range(c(x,y,z))
open3d()
plot3d(x,y,z)

# パラメタはu1,u2

paramlist<-c("u1","u2")

X<-list()
X[[1]]<-expression(cosh(u1)*cos(u2))
X[[2]]<-expression(cosh(u1)*sin(u2))
X[[3]]<-expression(sinh(u1))

dX<-list()

for(i in 1:length(paramlist)){
	dX[[i]]<-list()
	for(j in 1:length(X)){
		dX[[i]][[j]]<-deriv(X[[j]],paramlist[i])
	}
}

tmpu1<-tmpu2<-seq(from=-5,to=5,length=100)
u12<-expand.grid(tmpu1,tmpu2)
#u1<-u12[,1]
#u2<-u12[,2]
Xval<-matrix(0,length(u12[,1]),length(X))

for(i in 1:length(Xval[,1])){
	for(j in 1:length(Xval[1,])){
		u1<-u12[i,1]
		u2<-u12[i,2]
		Xval[i,j]<-eval(X[[j]])

	}
}

dXval<-list()
for(i in 1:length(paramlist)){
	dXval[[i]]<-matrix(0,length(u12[,1]),length(X))
	for(j in 1:length(dXval[[i]][,1])){
		for(k in 1:length(dXval[[i]][1,])){
			u1<-u12[j,1]
			u2<-u12[j,2]
			dXval[[i]][j,k]<-attr(eval(dX[[i]][[k]]),"gradient")[1]

		}
	}
}


#plot3d(Xval[[1]],Xval[[2]],Xval[[3]],col=rainbow(length(u1)))
plot3d(Xval,col="gray")
#plot3d(dXval[[1]][[1]],Xval[[1]][[2]],Xval[[1]][[3]],col=rainbow(length(u1)))
#plot3d(dXval[[2]][[1]],Xval[[2]][[2]],Xval[[2]][[3]],col=rainbow(length(u1)))



NselectedPt<-100

selected<-sample(1:length(Xval[,1]),NselectedPt)
segs1<-segs2<-matrix(0,NselectedPt*2,length(X))

for(i in 1:NselectedPt){
	tmpX<-Xval[selected[i],]
	tmpdX1<-dXval[[1]][selected[i],]
	tmpdX2<-dXval[[2]][selected[i],]
	segs1[2*i-1,]<-tmpX
	segs1[2*i,]<-tmpX+tmpdX1
	
	segs2[2*i-1,]<-tmpX
	segs2[2*i,]<-tmpX+tmpdX2
	
}
segments3d(segs1,col=2,lwd=3)
segments3d(segs2,col=3,lwd=3)
  • 外積ベクトルを付加しよう
# 外積の計算
library(MCMCpack)
# 複素数行列のDeterminantの計算用関数
detComplex<-function(M){
	e.out<-eigen(M)
	prod(e.out[[1]])
}
# 外積計算用関数
ExteriorProduct<-function(V){
	ret<-rep(0,length(V[1,]))
	for(i in 1:length(ret)){
		ret[i]<-(-1)^(i+1)*detComplex(V[,-i])
	}
	ret
}
# 例えばn=7次でやってみる
n<-7
# 適当に複素数を要素とする正方行列を作る
X<-matrix(complex(real = rdirichlet(1,rep(1,n^2)), imaginary = rdirichlet(1,rep(1,n^2))),ncol=n)
# Hermite化する
X<-t(Conj(X))%*%X
# Determinantを計算する
detX<-detComplex(X)
detX
# n個のベクトルから適当にn-1個を選ぶ
s<-sample(1:n,(n-1))
# 選ばれたn-1個のベクトルについて外積を計算する
ep<-ExteriorProduct(X[s,])
# 外積は長さnのベクトルである
ep
# 選ばれなかったベクトルと、選ばれたn-1個のベクトルの外積との内積を計算すると
# 選ばれなかったベクトルと選ばれたベクトルとが作る行列のDeterminantになっていることが以下の計算でわかる
sum(X[-s,]*ep)
detComplex(X)
sum(X[-s,]*ep)-detComplex(X)



# パラメタはu1,u2

paramlist<-c("u1","u2")

X<-list()
X[[1]]<-expression(cosh(u1)*cos(u2))
X[[2]]<-expression(cosh(u1)*sin(u2))
X[[3]]<-expression(sinh(u1))

dX<-list()

for(i in 1:length(paramlist)){
	dX[[i]]<-list()
	for(j in 1:length(X)){
		dX[[i]][[j]]<-deriv(X[[j]],paramlist[i])
	}
}

tmpu1<-tmpu2<-seq(from=-5,to=5,length=100)
u12<-expand.grid(tmpu1,tmpu2)
#u1<-u12[,1]
#u2<-u12[,2]
Xval<-matrix(0,length(u12[,1]),length(X))

for(i in 1:length(Xval[,1])){
	for(j in 1:length(Xval[1,])){
		u1<-u12[i,1]
		u2<-u12[i,2]
		Xval[i,j]<-eval(X[[j]])

	}
}

dXval<-list()
for(i in 1:length(paramlist)){
	dXval[[i]]<-matrix(0,length(u12[,1]),length(X))
	for(j in 1:length(dXval[[i]][,1])){
		for(k in 1:length(dXval[[i]][1,])){
			u1<-u12[j,1]
			u2<-u12[j,2]
			dXval[[i]][j,k]<-attr(eval(dX[[i]][[k]]),"gradient")[1]

		}
	}
}


#plot3d(Xval[[1]],Xval[[2]],Xval[[3]],col=rainbow(length(u1)))
plot3d(Xval,col="gray")
#plot3d(dXval[[1]][[1]],Xval[[1]][[2]],Xval[[1]][[3]],col=rainbow(length(u1)))
#plot3d(dXval[[2]][[1]],Xval[[2]][[2]],Xval[[2]][[3]],col=rainbow(length(u1)))



NselectedPt<-100

selected<-sample(1:length(Xval[,1]),NselectedPt)
segs1<-segs2<-segs3<-matrix(0,NselectedPt*2,length(X))

for(i in 1:NselectedPt){
	tmpX<-Xval[selected[i],]
	tmpdX1<-dXval[[1]][selected[i],]
	tmpdX2<-dXval[[2]][selected[i],]
	segs1[2*i-1,]<-tmpX
	segs1[2*i,]<-tmpX+tmpdX1
	
	segs2[2*i-1,]<-tmpX
	segs2[2*i,]<-tmpX+tmpdX2
	
	ep.out<-ExteriorProduct(rbind(tmpdX2,tmpdX1))
	
	segs3[2*i-1,]<-tmpX
	segs3[2*i,]<-tmpX+ep.out/sqrt(sum(ep.out^2))*sqrt(sum(tmpdX2^2))
	
	
}
segments3d(segs1,col=2,lwd=3)
segments3d(segs2,col=3,lwd=3)
segments3d(segs3,col=4,lwd=3)