２次元プロットする - ryamadaのコンピュータ・数学メモ

２つの「もの」がn次元ベクトルで表現されているとする
それぞれを $x = (x_1,...,x_n),y = (y_1,...,y_n)$ とする
空間の点と考えてユークリッド距離を計算すれば、 $euc.d = \sqrt{\sum_{i=1}^n (x_i-y_i)^2}$
これは、n次元空間を描き、そこに２点を配置して、２点間の直線を引くことで図示ことができる
別の図示の方法としては、x軸とy軸との２次元平面を準備して、そこに $(x_i,y_i)$ なる点を打って示すことである
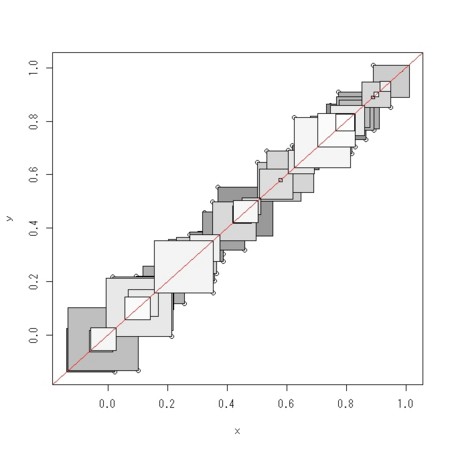
このとき $(x_i-y_i)^2$ というのは、点 $(x_i,y_i)$ と、その点が直線 $y=x$ に対して対称な点とを対角２点とする正方形の面積であるから、ユークリッド距離は、そのような正方形の面積の総和の平方根になる
正方形を描いてみると次のようになる

n <- 100
x <- runif(n)
y <- x + rnorm(n)*0.1
xlim <- ylim <- c(min(c(x,y)),max(c(x,y)))

plot(x,y,xlim=xlim,ylim=ylim)
for(i in 1:length(x)){
	col <- gray(0.5 + 0.5 * i/length(x))
	polygon(c(x[i],x[i],y[i],y[i]),c(y[i],x[i],x[i],y[i]),col=col)
}
abline(0,1, col=2)

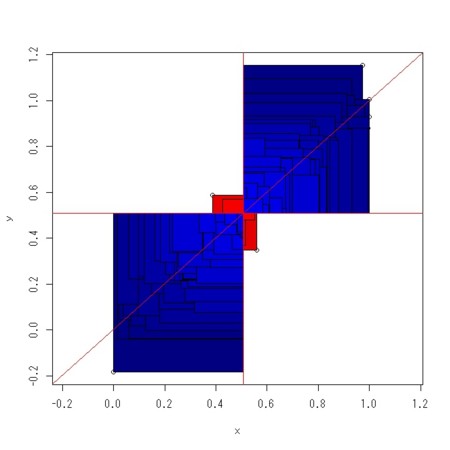
一方、相関係数は $\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{\sqrt{(\sum_{i=1}^n(x_i-\bar{x})^2)(\sum_{i=1}^n(y_i-\bar{y})^2)}}$ であるので、この分子の部分のみを同様に図示とすると、 $(\bar{x},\bar{y})$ という点(重心)と各点とが作る長方形の面積の和(ただし、重心を中心として直交４象限に分けたとき、第１、第３象限のときは正の値として加え、第２、第４象限のときは、負の値として加える、ことになるので、それを２色で塗り分けることにする

plot(x,y,xlim=xlim,ylim=ylim)

d.from.center <- sqrt((x-mean(x))^2+(y-mean(y))^2)
ord <- order(d.from.center,decreasing =TRUE)
cnt <- 1
for(i in ord){
	col <- sign((x[i]-mean(x))*(y[i]-mean(y)))+3
	col2 <- c(0,0,0)
	if(col == 2){
		col2 <- c(0.5+0.5*cnt/length(x),0,0)
	}else{
		col2 <- c(0,0,0.5+0.5*cnt/length(x))
	}
	cnt <- cnt +1
	polygon(c(mean(x),mean(x),x[i],x[i]),c(mean(y),y[i],y[i],mean(y)),col=rgb(col2[1],col2[2],col2[3]))
}
abline(mean(y)-mean(x),1, col=2)
abline(v = mean(x),col=2)
abline(h = mean(y),col=2)