2014-09-21

円によるスプライン曲線

R スプライン曲線曲率円

スプライン曲線というのがある(Wiki記事)
与えられた点を通り、点の間は多項式曲線でつなぎ、点においてk次の微分が等しくなるように(滑らかになるように)多項式係数を調整した曲線のこと
これを曲率の考え方、円の考え方に取り込んでみる
2次元平面に順序のある点列があるとする
相並ぶ３点を通る円は一意に描ける
相並ぶ３点をスライドすると、末端の２つの2点間以外は、二つの円を通る
ここで、二つの円を通る部分はこの2つの円の混合とすることとする
また、その2点が作るセグメントが次のセグメントと滑らかにつながるように混合比は、2点付近では(1,0),(0,1)とした上で、その増減微分が0であるような関数を与えてみよう

# ３点を通る円
# 円の中心座標、半径、３点の順序を考慮した角度を返す
my.circle <- function(X){
	x1 <- X[1,1]
	x2 <- X[2,1]
	x3 <- X[3,1]
	y1 <- X[1,2]
	y2 <- X[2,2]
	y3 <- X[3,2]
	rot <- 0
	if(y2-y1 ==0){
		rot <- 1
	x1 <- X[1,2]
	x2 <- X[2,2]
	x3 <- X[3,2]
	y1 <- X[1,1]
	y2 <- X[2,1]
	y3 <- X[3,1]
	}
	x <- 1/2 * 1/(y1*(x2-x3)+y2*(x3-x1)+y3*(x1-x2)) * ((y1-y2)*(y2-y3)*(y3-y1)-((y2-y3)*x1^2+(y3-y1)*x2^2+(y1-y2)*x3^2))
	y <- -(x2-x1)/(y2-y1)*(x-(x1+x2)/2) + (y1+y2)/2
	ctr <- c(x,y)
	if(rot==1){
		ctr <- c(y,x)
	}
	# 原点と３点とを結ぶ半径ベクトルの角を求める
	tmp <- (t(t(X)-ctr))
	angles <- Arg(tmp[,1] + 1i*tmp[,2])
	angles[which(angles<0)] <- angles[which(angles<0)] + 2*pi
	#print(angles)
	angle.dir <- 1
	if(angles[2] > angles[1]){
		if(angles[3] > angles[2]){
			
		}else{
			if(angles[3] < angles[1]){
				angles[3] <- angles[3] + 2*pi
			}else{
				angle.dir <- -1
				angles[2] <- angles[2] - 2*pi
				angles[3] <- angles[3] - 2*pi
			}
		}
	}else{
		if(angles[3] < angles[2]){
			angle.dir <- -1
		}else{
			if(angles[3] > angles[1]){
				angle.dir <- -1
				angles[3] <- angles[3] - 2*pi
			}else{
				angles[2] <- angles[2] + 2*pi
				angles[3] <- angles[3] + 2*pi
			}
		}
	}
	#print(angles)
	R <- sqrt(sum((X[1,]-ctr)^2))
	return(list(ctr=ctr,R=R,angles=angles,angle.dir=angle.dir))
}

# 隣接する４点には、２つの「３点を通る円」が描けて
# 中央２点は２つの円の両方に含まれる
# この２点の間に曲線を引き、２つの円を滑らかに移行させる
# そのために、２つの円の構成比を(u,1-u)でパラメタライズし
# u = -sin(k*pi-pi/2)/2 + 2 のようにkで表すこととする
# ただし、kは0から1へ動く関数

# この関数は隣接２円の寄与度に情報の濃さで重みづけをするなどの工夫をするのもよいだろうが、今はしない

k <- seq(from=0,to=1,length=100)
u <- -sin(k*pi-pi/2)/2 + 0.5
plot(k,u,type="l")

# 連続点行列から、円情報をシリアルに返す
my.serial.circles <- function(X){
	circles <- list()
	for(i in 1:(length(X[,1])-2)){
		circles[[i]] <- my.circle(X[i:(i+2),])
	}
	circles
}

# それを反映させて座標を計算
# Xは入力点
# Yは円での座標(セグメントに２つの座標が返される
# Zは２円のオーバーラップ部分を調整した座標を返す
# Wは調整座標と、調整が必要ない両端セグメント座標を合わせたもの
# W.serialはリストであるWを行列に置き換えたもの

my.circle.spline <- function(X,n=100){
	circles <- my.serial.circles(X)
	Y <- list()
	Z <- list()
	for(i in 1:length(circles)){
		tmp.t <- seq(from=circles[[i]]$angles[1],to=circles[[i]]$angles[3],length=n)
		tmp.x <- circles[[i]]$R * cos(tmp.t) + circles[[i]]$ctr[1]
		tmp.y <- circles[[i]]$R * sin(tmp.t) + circles[[i]]$ctr[2]
		Y[[i]] <- cbind(tmp.x,tmp.y)
	}
	k <- seq(from=0,to=1,length=n)
	u <- -sin(k*pi-pi/2)/2 + 0.5

	for(i in 1:(length(circles)-1)){
		tmp.t1 <- seq(from=circles[[i]]$angles[2],to=circles[[i]]$angles[3],length=n)
		tmp.t2 <- seq(from=circles[[i+1]]$angles[1],to=circles[[i+1]]$angles[2],length=n)
		tmp.x1 <- circles[[i]]$R * cos(tmp.t1) + circles[[i]]$ctr[1]
		tmp.y1 <- circles[[i]]$R * sin(tmp.t1) + circles[[i]]$ctr[2]
		tmp1 <- cbind(tmp.x1,tmp.y1)
		tmp.x2 <- circles[[i+1]]$R * cos(tmp.t2) + circles[[i+1]]$ctr[1]
		tmp.y2 <- circles[[i+1]]$R * sin(tmp.t2) + circles[[i+1]]$ctr[2]
		tmp2 <- cbind(tmp.x2,tmp.y2)
		Z[[i]] <- u*tmp1 + (1-u)*tmp2
	}
	W <- list()
	tmp.t <- seq(from=circles[[1]]$angles[1],to=circles[[1]]$angles[2],length=n)
	tmp.x <- circles[[1]]$R * cos(tmp.t) + circles[[1]]$ctr[1]
	tmp.y <- circles[[1]]$R * sin(tmp.t) + circles[[1]]$ctr[2]

	W[[1]] <- cbind(tmp.x,tmp.y)
	for(i in 1:length(Z)){
		W[[i+1]] <- Z[[i]]
	}
	N <- length(Y)
	tmp.t <- seq(from=circles[[N]]$angles[2],to=circles[[N]]$angles[3],length=n)
	tmp.x <- circles[[N]]$R * cos(tmp.t) + circles[[N]]$ctr[1]
	tmp.y <- circles[[N]]$R * sin(tmp.t) + circles[[N]]$ctr[2]
	W[[length(W)+1]] <- cbind(tmp.x,tmp.y)
	W.serial <- matrix(0,0,2)
	for(i in 1:length(W)){
		W.serial <- rbind(W.serial,W[[i]])
	}
	return(list(X=X,Y=Y,Z=Z,W=W,W.serial=W.serial))
}
# プロットする関数
plot.circle.spline <-function(cic.sp){
	xlim <- range(cic.sp$W.serial[,1])
	ylim <- range(cic.sp$W.serial[,2])
	plot(cic.sp$X,pch=20,xlim=xlim,ylim=ylim)
	points(cic.sp$W.serial,type="l",col=2)
}

# 曲率的スプライン曲線
tt <- sort(runif(10))*8
x <- tt*1.7
y <- sin(tt)
X <- cbind(x,y)

cic.sp <- my.circle.spline(X)
plot(cic.sp$X,asp=TRUE)
plot(cic.sp$X)
for(i in 1:length(cic.sp$Y)){
	points(cic.sp$Y[[i]],type="l")
}
for(i in 1:length(cic.sp$Z)){
	points(cic.sp$Z[[i]],type="l",col=2)
}

plot.circle.spline(cic.sp)


# 隣り合う２点のy座標が同じでも円が引けることを確認
x <- 1:6
y <- c(1,2.1,3,3,4.1,5.5)
X <- cbind(x,y)
cic.out2 <- my.circle.spline(X)
plot.circle.spline(cic.out2)

# 真実の曲線と、標本からのスプライン曲線を重ねて描く
t <- sort(runif(300))*10
X <- cbind(exp(t*0.1)*cos(t),exp(t*0.01)*sin(t))
s <- sort(sample(1:length(t),length(t)/10))
cic.sp3 <- my.circle.spline(X[s,])
plot.circle.spline(cic.sp3)
points(X,type="l",col=3)

# 別の曲線で
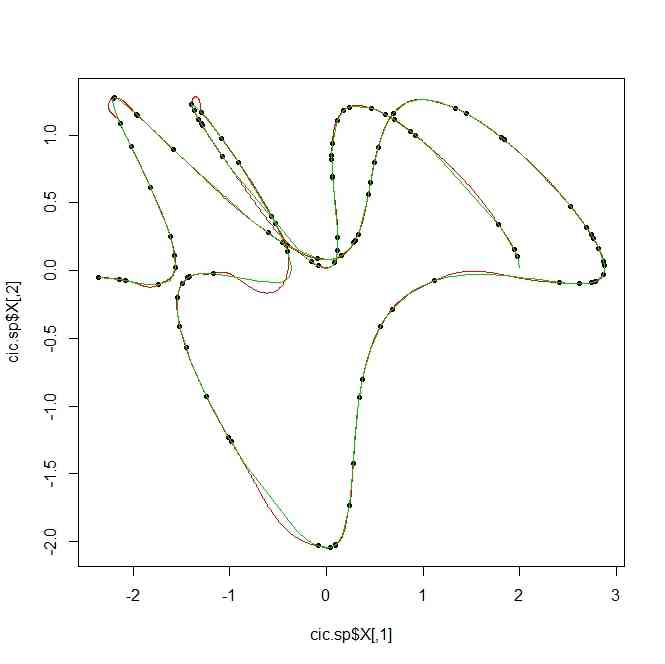
X <- cbind((exp(t*0.1)+cos(3*t))*cos(t),(exp(t*0.01)+sin(3*t))*sin(t))
s <- sort(sample(1:length(t),length(t)/3))

cic.sp4 <- my.circle.spline(X[s,])
plot.circle.spline(cic.sp4)
points(X,type="l",col=3)

# Y,Zなども描く
plot(cic.sp3$X,asp=TRUE)
plot(cic.sp3$X,type="l")
plot(cic.sp3$X,pch=20,cex=0.1)
for(i in 1:length(cic.sp3$Y)){
	points(cic.sp3$Y[[i]],type="l")
}
plot(cic.sp3$X,pch=20,cex=0.1)
plot(cic.sp3$X,type="l")
for(i in 1:length(cic.sp3$Z)){
	points(cic.sp3$Z[[i]],type="l",col=2)
}