2014-11-03

共形変換による２次元の形解析その３

共形変換形

昨日は共形変換の基本パーツについて図示して確認した
変換で回りすぎて重なるというようなことのない領域での変形データが得られたときに、その変換関数を推定する、ということを考えてみる
$f(z)= \sum_{i=0}^{n-1} a_i z^i$ という変換とする
係数推定なので、n個の複素数〜2n個の実数の推定になる
したがって、正確な変換値のペアがkペアあるときに、どうやって推定するかである。正確な変換ペアがあるということならば、であれば、条件としては十分になるだろうか
- ちなみに、メビウス変換は、３ペアで決定する
さて、今、 $f(z)=w= \sum_{j=0}^{n-1} a_j z^n$ を考える
$z=zx +i zy, w = wx+ i wy,a = ax + i ay$ として、虚実を分ければ
$\sum_{j=0}^{n-1} (zx ax - zy ay) = wx$ , $\sum_{j=0}^{n-1} (zy ax + zx ay) = wy$ が成り立つ
これを、(2n)x(2n)の行列と長さ2nのベクトルで表せば、単に、線形代数計算で係数が決まる

my.grid <- function(X=(-10):10,Y=(-10):10,n=200){
	x=seq(from=min(X),to=max(X),length=n+1)[-1]
	y=seq(from=min(Y),to=max(Y),length=n+1)[-1]
	as.matrix(rbind(expand.grid(x,Y),expand.grid(X,y)))
}
xy <- my.grid(X=(-10):10,Y=(-10):10,n=1000)
z <- xy[,1] + 1i * xy[,2]
col <- rep(1,length(z))
col[which(Re(z)==0)] <- 2
col[which(Im(z)==0)] <- 2
col[which(abs(Re(z))==abs(max(Re(z))))] <- 3
col[which(abs(Im(z))==abs(max(Im(z))))] <- 3
plot(z,pch=20,cex=0.5,col=col)

# f(z) = az + b
a <- 4+1i*2
b <- 2+1i*3
zz <- a*z+b
# n点

n <- 2
s <- sample(1:length(z),n)
zn <- z[s]
wn <- zz[s]

my.conformal.coef <- function(zn,wn){
	n <- length(zn)
	W <- c(Re(wn),Im(wn))
	Z <- matrix(0,2*n,2*n)
	for(i in 1:n){
		tmp <- zn[i]^(0:(ｎ-1))
		Z[i,] <- c(Re(tmp),-Im(tmp))
		Z[n+i,] <- c(Im(tmp),Re(tmp))
		Z[i,ｎ+1] <- Z[n+i,1] <- 0
	}
	solve(Z) %*% W
	# lm(W~Z-1)

}
my.conformal.coef(zn,wn)

> my.conformal.coef(zn,wn)
     [,1]
[1,]    2
[2,]    4
[3,]    3
[4,]    2

結局、複素数のべきについての線形代数なので、線形回帰関数を使ってもよさそうだ
- モデルよりも複雑なモデル設定で計算すると、その部分に係数はつくが、0に近い値が返ってきたりしていて、よい感じ

my.conformal.coef.2 <- function(zn,wn,k=2){
	n <- length(zn)
	W <- c(Re(wn),Im(wn))
	z.re <- Re(zn)
	z.im <- Im(zn)
	Z <- matrix(0,2*n,2*k)
	for(i in 1:n){
		tmp <- z[i]^(0:(k-1))
		Z[i,] <- c(Re(tmp),-Im(tmp))
		Z[n+i,] <- c(Im(tmp),Re(tmp))
		Z[i,k+1] <- Z[n+i,1] <- 0
	}
	#solve(Z) %*% W
	lm(W~Z-1)

}

格子が２つの共形変換で変わったとする

as <- runif(5) + runif(5) * 1i
as.2 <- runif(3)+runif(3) * 1i
xy <- my.grid(X=10:20,Y=10:20,n=1000)
z <- xy[,1] + 1i * xy[,2]

z. <- z + rnorm(length(z))*0.1+ 1i*rnorm(length(z))*0.1
z.2 <- z + rnorm(length(z))*0.1+ 1i*rnorm(length(z))*0.1
zz <- as[1]
for(i in 2:length(as)){
	zz <- zz + as[i] * z.^(i-1)
}
zz.2 <- as.2[1]
for(i in 2:length(as.2)){
	zz.2 <- zz.2 + as.2[i] * z.2^(i-1)
}

#zz. <- zz + rnorm(length(zz))*1 + 1i * rnorm(length(zz))*1
zz. <- zz
par(mfcol=c(1,2))
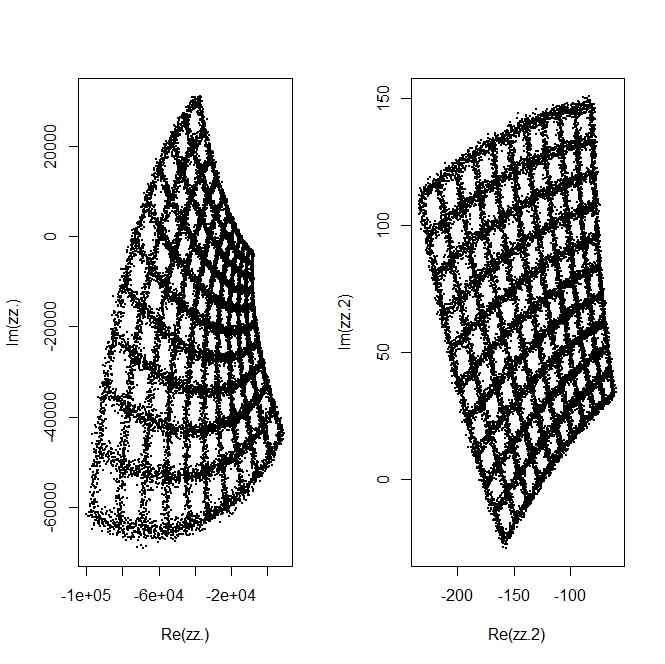
plot(zz.,pch=20,cex=0.1)
plot(zz.2,pch=20,cex=0.1)
par(mfcol=c(1,1))

これの間を取り持つ共形変換を推定してみる

as <- runif(5) + runif(5) * 1i
as.2 <- runif(3)+runif(3) * 1i
xy <- my.grid(X=10:20,Y=10:20,n=1000)
z <- xy[,1] + 1i * xy[,2]

z. <- z + rnorm(length(z))*0.1+ 1i*rnorm(length(z))*0.1
z.2 <- z + rnorm(length(z))*0.1+ 1i*rnorm(length(z))*0.1
zz <- as[1]
for(i in 2:length(as)){
	zz <- zz + as[i] * z.^(i-1)
}
zz.2 <- as.2[1]
for(i in 2:length(as.2)){
	zz.2 <- zz.2 + as.2[i] * z.2^(i-1)
}

#zz. <- zz + rnorm(length(zz))*1 + 1i * rnorm(length(zz))*1
zz. <- zz
par(mfcol=c(1,2))
plot(zz.,pch=20,cex=0.1)
plot(zz.2,pch=20,cex=0.1)
par(mfcol=c(1,1))

coef.out <- my.conformal.coef.2(zz.,zz.2,k=6)
coef.out$coef


coef.mat <- matrix(coef.out$coef,ncol=2)
as.new <- coef.mat[,1]+coef.mat[,2]*1i
zz.new <- as.new[1]
for(i in 2:length(as.new)){
	zz.new <- zz.new + as.new[i]*zz.^(i-1)
}
par(mfrow=c(2,2))
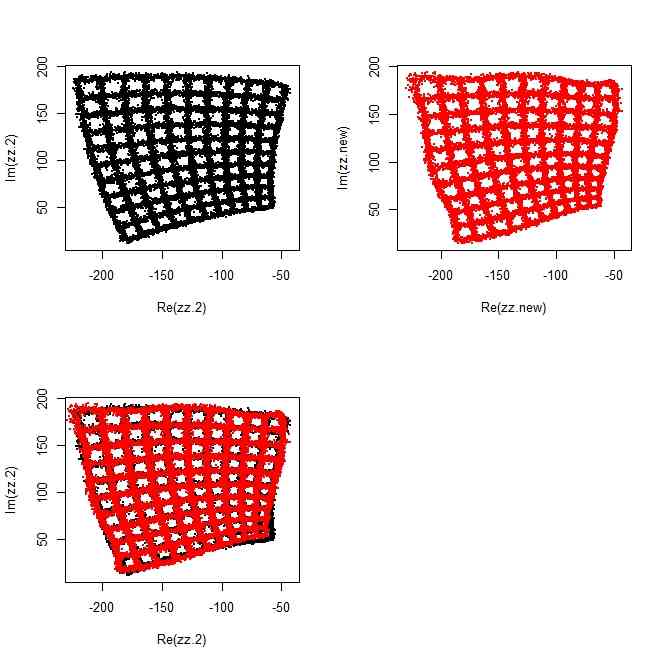
plot(zz.2,pch=20,cex=0.1)
plot(zz.new,pch=20,cex=0.1,col=2)
plot(zz.2,pch=20,cex=0.1)
points(zz.new,pch=20,cex=0.1,col=2)
par(mfrow=c(1,1))

予測に用いる点の数が少なくても、何とかなることも示す

as <- runif(5) + runif(5) * 1i
as.2 <- runif(3)+runif(3) * 1i
xy <- my.grid(X=10:20,Y=10:20,n=1000)
z <- xy[,1] + 1i * xy[,2]

z. <- z + rnorm(length(z))*0.1+ 1i*rnorm(length(z))*0.1
z.2 <- z + rnorm(length(z))*0.1+ 1i*rnorm(length(z))*0.1
zz <- as[1]
for(i in 2:length(as)){
	zz <- zz + as[i] * z.^(i-1)
}
zz.2 <- as.2[1]
for(i in 2:length(as.2)){
	zz.2 <- zz.2 + as.2[i] * z.2^(i-1)
}

#zz. <- zz + rnorm(length(zz))*1 + 1i * rnorm(length(zz))*1
zz. <- zz
par(mfcol=c(1,2))
plot(zz.,pch=20,cex=0.1)
plot(zz.2,pch=20,cex=0.1)
par(mfcol=c(1,1))

coef.out <- my.conformal.coef.2(zz.,zz.2,k=6)
coef.out$coef


coef.mat <- matrix(coef.out$coef,ncol=2)
as.new <- coef.mat[,1]+coef.mat[,2]*1i
zz.new <- as.new[1]
for(i in 2:length(as.new)){
	zz.new <- zz.new + as.new[i]*zz.^(i-1)
}
par(mfrow=c(2,2))
plot(zz.2,pch=20,cex=0.1)
plot(zz.new,pch=20,cex=0.1,col=2)
plot(zz.2,pch=20,cex=0.1)
points(zz.new,pch=20,cex=0.1,col=2)
par(mfrow=c(1,1))

n <- length(z)/10

s <- sample(1:length(z),n)
zn <- z[s]
wn <- zz.[s]

plot(wn,pch=20,cex=0.1)

my.conformal.coef.2(zn,wn,k=length(as))
as



coef.out <- my.conformal.coef.2(zz.,zz.2,k=6)

s <- sample(1:length(zz.),100)
coef.out.s <- my.conformal.coef.2(zz.[s],zz.2[s],k=6)
coef.out$coef
coef.out.s$coef


coef.mat <- matrix(coef.out$coef,ncol=2)
coef.mat.s <- matrix(coef.out$coef,ncol=2)
as.new <- coef.mat[,1]+coef.mat[,2]*1i
as.new.s <- coef.mat.s[,1] + coef.mat.s[,2]*1i
zz.new <- as.new[1]
zz.new.s <- as.new.s[1]
for(i in 2:length(as.new)){
	zz.new <- zz.new + as.new[i]*zz.^(i-1)
	zz.new.s <- zz.new.s + as.new.s[i]*zz.^(i-1)
}
par(mfrow=c(2,2))
plot(zz.2,pch=20,cex=0.1)
plot(zz.new,pch=20,cex=0.1,col=2)
plot(zz.2,pch=20,cex=0.1)
points(zz.new,pch=20,cex=0.1,col=2)
plot(zz.2,pch=20,cex=0.1)
points(zz.new.s,pch=20,cex=0.1,col=3)
par(mfrow=c(1,1))