曲線に伴う共形変換 - ryamadaのコンピュータ・数学メモ

駆動関数によって実直線上を動く。これが駆動関数となって、ある曲線が複素上半平面を伸びることに対応する。
その曲線を除いた複素上半平面を、曲線部分も含めた複素上半平面全体に写す変換が存在して、それは共形変換であることが知られている
実際、この複素上半平面に伸びる曲線の頂点が、その曲線が定める共形変換によって、実軸上の点に移される(極限として移される)
$\frac{\partial g_t(z)}{\partial t} = \frac{2}{g_t(z)-Ut}$ と言う微分方程式によってこの共形変換は変化していく
ただしt=0のときの変換は、 $g_0(z)=z$ 、すなわち恒等変換とする
駆動関数 $Ut$ を実軸上のブラウン運動とするとそれはSLE
この共形変換がわかれば、実軸上の動きから複素上半平面上の曲線が、「共形変換の逆変換」を実軸上の点に施すことで描ける(ただし、共形変換自体が微分方程式になっているので、複素上半平面上の点が共形変換でどこに移るか、は近似的に求められるが、その逆は、共形変換関数を出してやらないと、ちょっと難しい。その関数は、級数展開した形でなら、漸化式を使って定義されているので、「実軸上の動き」→「曲線」という処理は、少々大変
やってみる(複素上半平面上の点が共形変換でどこに移るかの時系列変化、という簡単な方)

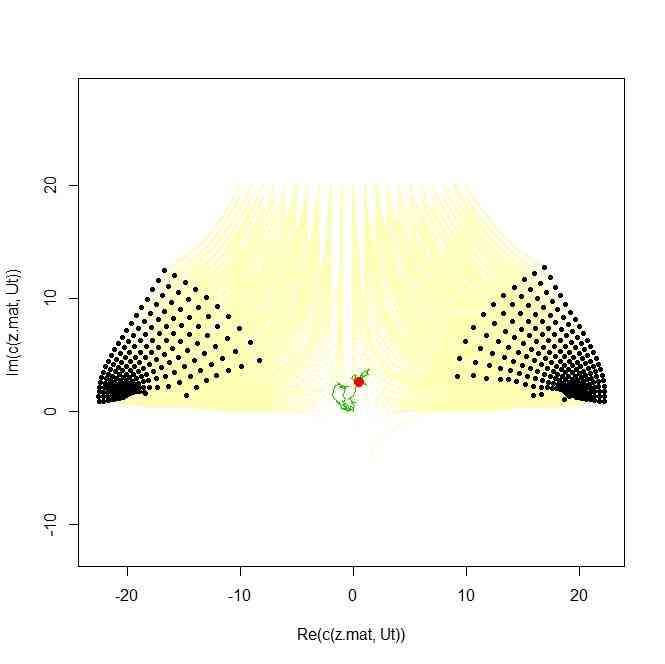
緑の線が酔歩(赤い点はその先頭)
黒い点は「スタート時は格子点」だったものが、変換によって移動した先の点
薄いクリーム色の線は、その動きをトレースしたもの(と曲線のトレース)の全体(全体というのは曲線を最後まで移動して、それに対応する共形変換の結果を描いたもの)
この共形変換は微分方程式を近似的に追いかける(以下のソース)もできるが、漸化式で表現された無限級数表現も知られている(こちらで未消化なりにメモしてある)

k <- 6
n <- 100
#BM1 <- sample(c(-1,1),n,replace=TRUE)*0.5
#BM2 <- sample(c(-1,1),n,replace=TRUE)*0.5
BM1 <- rnorm(n,0,0.1)
BM2 <- rnorm(n,0,0.1)
Ut1 <- cumsum(BM1)
Ut1 <- c(0,Ut1)
Ut2 <- cumsum(BM2)
Ut2 <- c(0,Ut2)
Ut2 <- abs(Ut2)
#Ut <- sqrt(k) * (Ut1 + 1i * Ut2)
Ut <- sqrt(k) * (Ut1) + 1i*0

plot(Ut)

z <- 10 + 1i * 10
z.lattice <- expand.grid((-10):10,(0:20))
z.lattice <- z.lattice[,1] + 1i * z.lattice[,2]
z.mat <- matrix(0,n+1,length(z.lattice))
zs <- rep(0,n+1)
zs[1] <- z
z.mat[1,] <- z.lattice
for(i in 1:n){
	dz <- 2/(zs[i]-Ut[i])
	zs[i+1] <- zs[i] + dz
	dzs <- 2/(z.mat[i,]-Ut[i])
	z.mat[i+1,] <- z.mat[i,] + dzs
}
plot(zs)
#matplot(z.mat,type="l")
for(i in 1:(n+1)){
	plot(c(z.mat,Ut),asp=TRUE,pch=20,cex=0.1,col=rgb(1,1,0.7))

	points(z.mat[i,],pch=20)
	points(Ut[1:i],type="l",col=3,pch=20)
	points(Ut[i],col=2,pch=20,cex=2)
}