- SLEはブラウン運動が駆動する曲線
- その離散版にSchwarz-Christoffel変換に対応する共形変換の繰り返しが生成する折れ線がある
- Schwartz-Christoffel変換は、多角形を複素上半平面と対応付ける変換(こちら)
- 量子状態のブラウン運動的変化を量子ウォークと言うが、それはユニタリ変換だと言い、それを説明する文書にこのSchwarz-Christoffelによる折れ線生成が書いてある(こちら)
- その文書の中に折れ線生成のパラメタκが出てきて、8とかが意味のある値らしいのだが、そについてはわからないなりに、パラメタを入れて、折れ線生成はできた
- Rソース
my.schwarzChristoffel <- function(p,n,S0=0+0*1i){
rw <- sample(c(-1,1),n,replace=TRUE) * p + 1/2 + 0 * 1i
my.S <- function(z,a){
z <- z + 0*1i
(z+2*sqrt((1-a)/a))^(1-a)*(z-2*sqrt(a/(1-a)))^a
}
S0 <- 0 + 0 * 1i
Ss <- rep(0,n)
for(i in 1:n){
if(i == 1){
Ss[i] <- my.S(S0,rw[i])
}else{
Ss[i] <- S0
for(j in i:1){
Ss[i] <- my.S(Ss[i],rw[j])
}
}
}
Ss
}
ps <- seq(from=0.05,to = 0.45,length=3)
ps <- 0.4
n.iter <- 5
n <- 200
out <- matrix(0,length(ps)*n.iter,n)
cnt <- 1
col <- c()
for(i in 1:length(ps)){
for(j in 1:n.iter){
out[cnt,] <- my.schwarzChristoffel(ps[i],n)
cnt <- cnt + 1
col <- c(col,i)
}
}
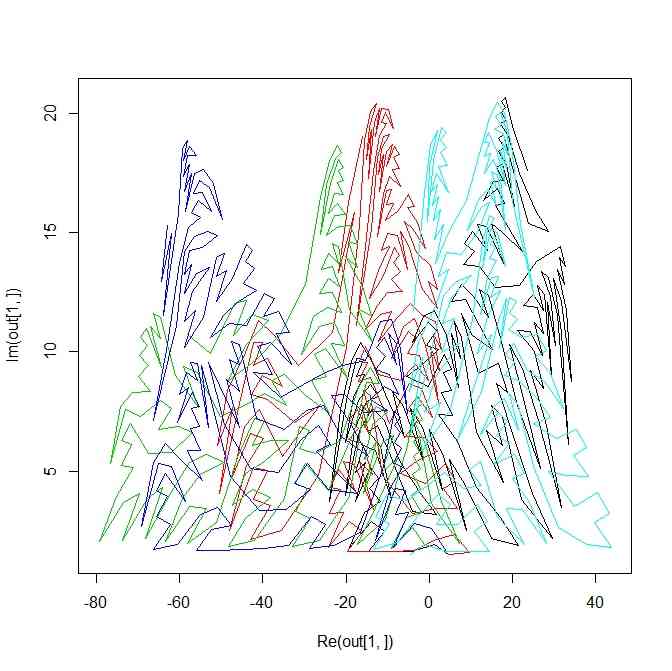
plot(out[1,],type="l",xlim = range(Re(out)),ylim=range(Im(out)),col=col[1])
for(i in 2:length(out[,1])){
points(out[i,],type="l",col=i)
}
a <- seq(from=0,to=1,length=10000)
a <- a[-c(1,100)] + 0*1i
(2*sqrt((1-a)/a))^(1-a) * (-2*sqrt(a/(1-a)))^a -> p
plot(p)
