SLE曲線の共形変換 - ryamadaのコンピュータ・数学メモ

SLE曲線では実軸上の関数 $Ut$ を駆動関数として、複素数を変換する共形変換 $g_t(z)$ に $\frac{\partial g_t(z)}{\partial t}=\frac{2}{g_t(z)-Ut}$ なる微分方程式を立てている
今、ある時刻tに $Ut$ なる値を駆動関数が取っているとする。 $g_t$ によって曲線の先端が、実軸上の点(Ut,0)に共形変換されている。
ではこの微分方程式はどうなっているかを、この時刻におけるある複素平面上の点 $z=a+i b$ についてみてみる
$\frac{2}{z-Ut}=\frac{2}{(a-Ut)+ib}=\frac{2((a-Ut)-ib)}{(a-Ut)+ib)((a-Ut)-ib)}=\frac{2((a-Ut)-ib)}{(a-Ut)^2+b^2}$ となるから
zの共形変換は、Utを中心とした共役複素数 $a-Ut - ib$ の方向に向かう。その向かう勢いは、分母が、上式の平方根であったなら、zによらず長さ２のベクトルに相当するが、分母は複素数の長さの二乗なので、中心Utに近ければ近いほど、勢いが強く、遠ければ遠いほど、向きはあっても勢いはない…双曲線

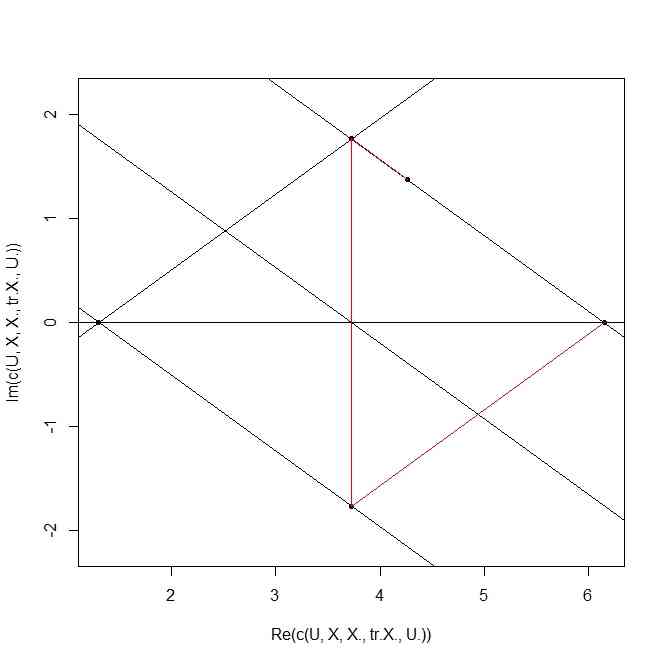
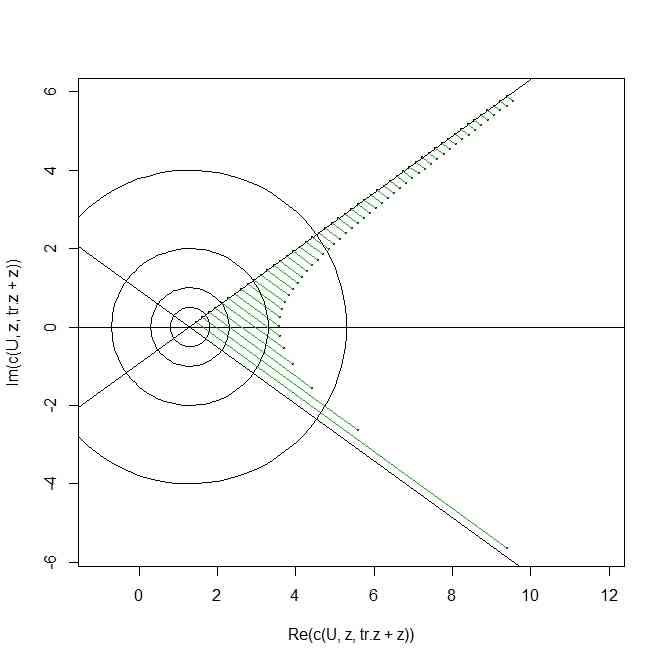
U <- 1.3 + 1i*0
theta <- pi/5
k <- 3
X <- U + k * cos(theta) + 1i * k * sin(theta)
X. <- U + k * cos(theta) - 1i * k * sin(theta)
tr.X <- 2/(X-U)
tr.X. <- tr.X + X
U. <- U + 2*(Re(X)-U) + 1i * 0
plot(c(U,X,X.,tr.X.,U.),pch=20,asp=TRUE)
abline(h=0)
abline(-U*tan(theta),tan(theta))
abline(U*tan(theta),-tan(theta))
abline(Im(X) + U*tan(theta),-tan(theta))
abline(2*Im(X) + U*tan(theta),-tan(theta))
segments(Re(X),Im(X),Re(X.),Im(X.),col=2)
segments(Re(X),Im(X),Re(tr.X.),Im(tr.X.),col=2)
segments(Re(X.),Im(X.),Re(U.),Im(U.),col=2)

x <- seq(from=0,to=10,length=50)
z <- U + x * cos(theta) + 1i * x * sin(theta)

plot(z)

tr.z <- 2/(z-U)
plot(c(U,z,tr.z+z),pch=20,cex=0.3,asp=TRUE)
abline(h=0)
abline(-U*tan(theta),tan(theta))
abline(U*tan(theta),-tan(theta))
for(i in 1:length(x)){
	segments(Re(z[i]),Im(z[i]),Re(tr.z[i]+z[i]),Im(tr.z[i]+z[i]),col=3)
}
t <- seq(from=0,to=2*pi,length=100)
rs <- c(0.5,1,2,4)
for(i in 1:length(rs)){
	points(U+rs[i]*cos(t),rs[i]*sin(t),type="l")
}