微分形式と曲線

• 外積代数は、n個の線形独立なベクトルに対しての要素が作る代数系
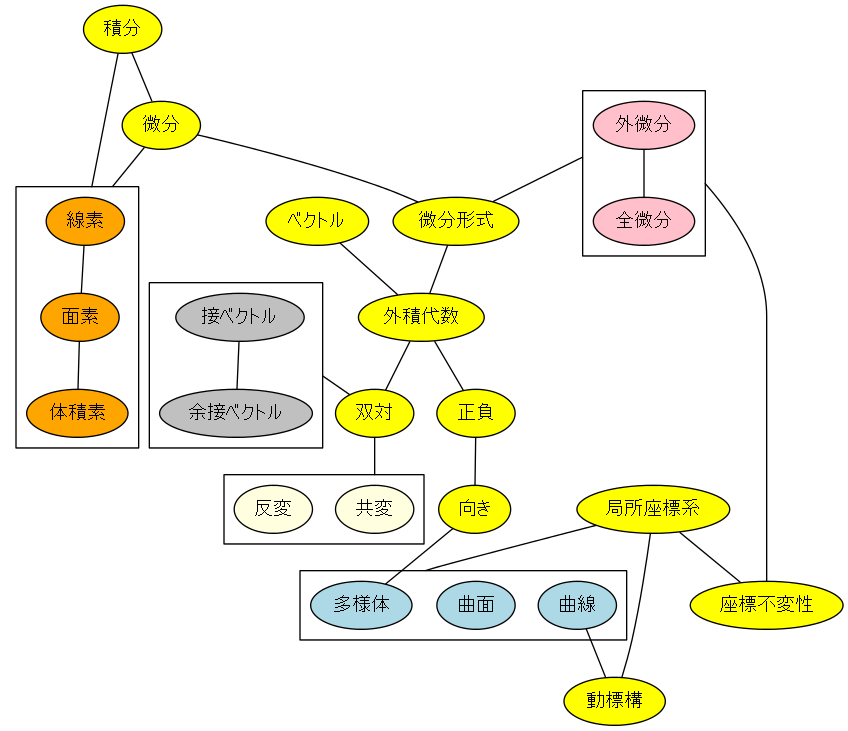
  • その特徴として
    • 正負・向きの存在
    • 階層性
    • 階層の対称性と関係の深い双対構造
• 外積代数を微分の線素ベクトルに用いると微分形式
• 微分形式は外積代数の構成を持つが、その階層を上るのが外微分
  • 外微分の第１階はいわゆる全微分
  • 外微分は座標不変
• 多様体には接線・接面がある
  • 接面は多様体上の局所座標系を持つ
  • Moving Frame(動標構)は曲線上の正規直交局所座標系
  • 多様体は幾何対象であるが、それを外積代数で表せば、双対の存在から２通りの表し方がある。それと関係するのが、接ベクトル・余接ベクトル
  • 多様体を微分すれば、そこには微分形式があって、その外微分は座標不変
• 双対
  • 対称性な外積代数
  • 正負のルール
    • 行列のdeterminantの正負
  • 多様体では向き
  • 接と余接
  • 反変と共変

graph g {
graph [compound=true];
graph [charset="UTF-8",fontname="MS UI Gothic"];
node[charset="UTF-8",fontname="MS UI Gothic"];

subgraph cluster1 {
node[charset="UTF-8",fontname="MS UI Gothic",style=filled,fillcolor="orange"]
線素;
面素;
体積素;	
}
subgraph cluster2 {
node[charset="UTF-8",fontname="MS UI Gothic",style=filled,fillcolor="lightblue"]
曲線;
曲面;
多様体;
}
subgraph cluster3 {
node[charset="UTF-8",fontname="MS UI Gothic",style=filled,fillcolor="gray"]
接ベクトル;
余接ベクトル;
}
subgraph cluster4 {
node[charset="UTF-8",fontname="MS UI Gothic",style=filled,fillcolor="pink"]
全微分;
外微分;
}
subgraph cluster5 {
node[charset="UTF-8",fontname="MS UI Gothic",style=filled,fillcolor="lightyellow"]
共変;
反変;
}
node[charset="UTF-8",fontname="MS UI Gothic",style=filled,fillcolor="yellow"];

edge[charset="UTF-8",fontname="MS UI Gothic"];
外積代数--双対;
外積代数--正負--向き--多様体[ltail=向き,lhead=多様体];
ベクトル--外積代数;
微分--微分形式--外積代数;
微分--線素[ltail=微分,lhead=cluster1];
線素--面素--体積素;
外微分--全微分;
外微分--微分形式[ltail=cluster4,lhead=微分形式];
局所座標系--座標不変性;
局所座標系--多様体[ltail=局所座標系,lhead=cluster2];
局所座標系--動標構;
曲線--動標構;
曲面;
積分--微分;
積分--線素[ltail=積分,lhead=cluster1];
接ベクトル--余接ベクトル;
接ベクトル--双対[ltail=cluster3,lhead=双対];
外微分--座標不変性[ltail=cluster4,lhead=座標不変性];
双対--共変[ltail=双対,lhead=cluster5];
}

>dot -Kdot -Tpng curve.dot -o curve.png