2014-08-17

初心に戻って、貝

R 射影幾何

貝や卵などの形のことをいじるのに、外積代数やら楕円関数やら、ボルツマン等式やらやったけれど、夏休みも終わりなので、元に戻って、貝
条件

> M
            [,1]       [,2]        [,3]       [,4]
[1,]  1.36836505  0.1216459  0.63585608 -0.5854620
[2,] -0.41765962 -1.7889032  0.21444323  0.6672658
[3,] -0.07303386 -0.9380238  0.03986569 -1.1766080
[4,] -0.47066985  0.4180992 -0.71966843 -1.5985446
> K
           [,1]       [,2]       [,3]       [,4]
[1,] -0.1824658  0.2464699 -1.9201338 -2.9316963
[2,]  0.1786383 -0.6043951  0.9368007  0.2924991
[3,]  1.6589981  0.4654187  0.9734282 -0.6336958
[4,] -0.8191066  0.3975617 -0.8525419 -1.1676240
> x.init
[1] 0.3021678 0.5662305 0.5802933 0.2742637
> x.step
[1]  0.07645100 -0.15417863  0.05908368 -0.07654749

exp.m <- function(A,n){
  # 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	#B <- diag(eigen.out[[1]]^n)
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}
d <- 4
K <- matrix(rnorm(d^2),d,d)

M <- matrix(0,d,d)
a <- 0.9
theta <- pi/7
M[1,1] <- a*cos(theta)
M[1,2] <- -a * sin(theta)
M[2,1] <- -M[1,2]
M[2,2] <- M[1,1]
M[3,3] <- M[4,4] <- 1.1
M. <- matrix(rnorm(d^2),d,d)
M <- M. %*% M

ks <- c(1,1.1,1.2,1.3)
t <- seq(from=-10,to=10,length=1000)

X <- matrix(0,length(t),d)
x.init <- runif(d)

XX <- matrix(0,0,d)

x.step <- rnorm(d)*0.1
n.iter <- 50
for(ii in 1:n.iter){
	x.init. <- x.init + x.step*ii*0.2
for(i in 1:length(t)){
	X[i,] <- Re(exp.m(M,t[i])[[1]]) %*% x.init.
}
XX <- rbind(XX,X)
}
Y <- t(K %*% t(XX))

Z <- matrix(0,length(XX[,1]),d-1)
for(i in 1:(d-1)){
	Z[,i] <- Y[,i]/Y[,d]
}
library(rgl)
plot3d(Z)

> K
          [,1]       [,2]       [,3]       [,4]
[1,] 0.8660254 -0.2886751 -0.2886751 -0.2886751
[2,] 0.0000000  0.8164966 -0.4082483 -0.4082483
[3,] 0.0000000  0.0000000  0.7071068 -0.7071068
[4,] 0.5000000  0.5000000  0.5000000  0.5000000
> M
             [,1]          [,2]  [,3]  [,4]
[1,] 6.123032e-17 -1.000000e+00 0.000 0e+00
[2,] 1.000000e+00  6.123032e-17 0.000 0e+00
[3,] 0.000000e+00  0.000000e+00 0.001 0e+00
[4,] 0.000000e+00  0.000000e+00 0.000 1e-05
> x.init
[1]  0.9625924  0.4525413  0.3824642 10.4457921

exp.m <- function(A,n){
  # 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	#B <- diag(eigen.out[[1]]^n)
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}
d <- 4
CategoryVector<-function(d){
  df <- d - 1
  diagval <- 1:d
  diagval <- sqrt((d)/df) * sqrt((d - diagval)/(d - diagval + 1))
  others <- -diagval/(d - (1:d))
  m <- matrix(rep(others, d), nrow = d, byrow = TRUE)
  diag(m) <- diagval
  m[upper.tri(m)] <- 0
  as.matrix(m[, 1:df])
}
make.simplex.0 <- function(k){
  cv <- CategoryVector(k)
  rbind(t(cv*sqrt(1-1/k)),rep(1/sqrt(k),k))
}
K <- make.simplex.0(d)
M <- matrix(0,d,d)
a <- 1
theta <- pi/2
M[1,1] <- a*cos(theta)
M[1,2] <- -a * sin(theta)
M[2,1] <- -M[1,2]
M[2,2] <- M[1,1]
M[3:4,3:4] <- diag(c(0.9,0.85))

a2 <- 1.0001
theta2 <- pi/2
M[3,3] <- a2*cos(theta2)
M[3,4] <- -a2 * sin(theta2)
M[4,3] <- -M[3,4]
M[4,4] <- M[3,3]
M[3:4,3:4] <- diag(c(0.001,0.00001))


#M. <- matrix(rnorm(d^2),d,d)
#M <- M. %*% M

ks <- c(1,1.1,1.2,1.3)
#M <- diag(ks)

t <- seq(from=-1000,to=3000,length=1000)

X <- matrix(0,length(t),d)
x.init <- runif(d)
x.init[d] <- x.init[d]+10

XX <- matrix(0,0,d)

x.step <- runif(d)*1
n.iter <- 1
for(ii in 1:n.iter){
	x.init. <- x.init + x.step*ii*10
	#x.init. <- runif(d)*5
	#x.init.[d] <- x.init.[d]+10

for(i in 1:length(t)){
	X[i,] <- Re(exp.m(M,t[i])[[1]] %*% x.init.)
}
XX <- rbind(XX,X)
}

#K[d,1:2] <- 0

Y <- t(K %*% t(XX))

Z <- matrix(0,length(XX[,1]),d-1)
for(i in 1:(d-1)){
	Z[,i] <- Y[,i]/Y[,d]
}
library(rgl)
Z. <- Z
Z. <- rbind(Z.,rep(min(Z),d-1))
Z. <- rbind(Z.,rep(max(Z),d-1))
plot3d(Z.)
K. <- t(K)/K[d,]

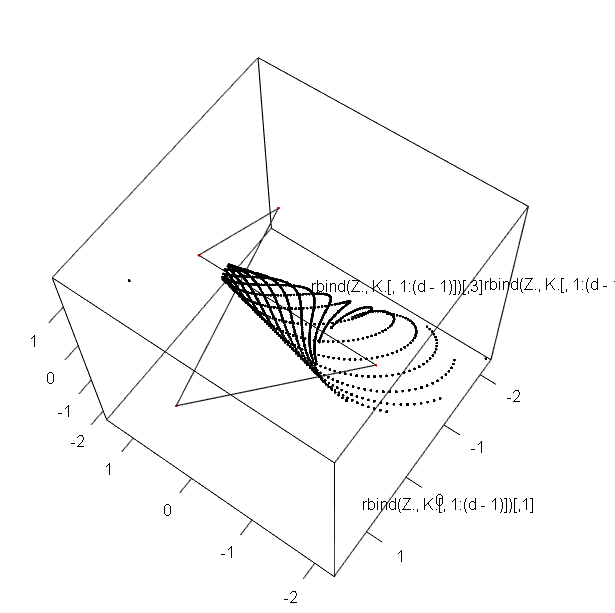
plot3d(rbind(Z.,K.[,1:(d-1)]),col=c(rep(1,length(Z.[,1])),rep(2,length(K.[,1]))))
points3d(K.[,1:(d-1)],col=4)
lines3d(rbind(K.[,1:(d-1)],K.[1,1:(d-1)]))