2014-06-16

複比数列から常微分方程式の逆演算

２変量常微分方程式が射影幾何を通じて複比を保存する数列を生じることを昨日の記事で示した
今日は、複比を満足する数列からその常微分方程式を逆演算したい
複比数列の両端収束値を、数列から複比を求め(推定し)る
これにより幾何的射影変換図の３つの点がわかる(もう一つの点は原点)
ここに、時間が経つと収束していく先である点と原点を結ぶ線分の上に適当に点をとる
これを射影変換における１つの光源とする(もう一つの光源は原点)
この光源と、別の収束点(これが「時間的には過去」の出発点)とを結ぶ直線が、「射影変換のもう一つの射影平面」である
この第二の射影平面上の点の座標を求める
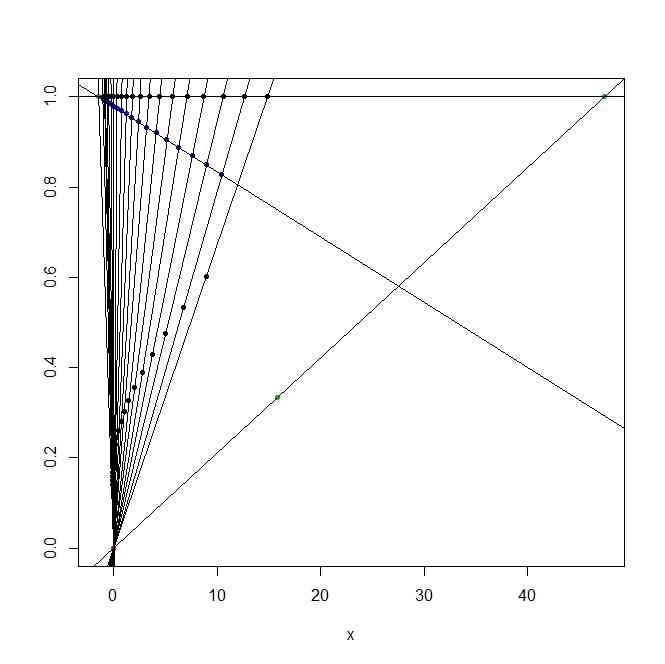
描いてみる

my.matrix.eigen <- function(lambdas,vs){
  Vs <- t(t(vs) * lambdas)
	Vs %*% solve(vs)
}

exp.m <- function(A,n){
  # 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	#B <- diag(eigen.out[[1]]^n)
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}

my.doubleratio <- function(x){
	if(!is.matrix(x)){
		x <- matrix(x,nrow=length(x))
	}
	P <- x[1:(length(x[,1])-3),]
	Q <- x[4:length(x[,1]),]
	S <- x[2:(length(x[,1])-2),]
	R <- x[3:(length(x[,1])-1),]
	((P-R)/(Q-R))/((P-S)/(Q-S))
}
n.iter <- 50
dr.calcs.min <- dr.calcs.max <- drs <- rep(0,n.iter)

for(ii in 1:n.iter){
	lambdas <- c(runif(1),runif(1)*3)
	vs <- matrix(rnorm(4)*10,2,2)
	A <- my.matrix.eigen(lambdas,vs)
	# 等間隔なt
	t <- seq(from=-5,to=5,length=20)
	X <- matrix(0,length(t),length(A[,1]))
	X.init <- runif(2)
	for(i in 1:length(t)){
	  X[i,] <- exp.m(A,t[i])[[1]] %*% X.init
	}
	x <- X[,1]/X[,2]
	plot(Re(x))
	dr.calc <- my.doubleratio(x)

	delta <- t[2]-t[1]
	k1 <- lambdas[1]
	k2 <- lambdas[2]
	delta.k <- k1-k2
	dr <- (exp(delta.k/2*delta) + exp(-delta.k/2*delta))^2
	dr.calcs.min[ii] <- min(dr.calc)
	dr.calcs.max[ii] <- max(dr.calc)
	drs[ii] <- dr
}

plot(data.frame(dr.calcs.min,dr.calcs.max,drs))

# データから複比を出す
dr <- my.doubleratio(x)

# その収束値を推定する
my.doubleratio.next <- function(x,m){
	((1-m)*x[2]*x[3]+m*x[1]*x[3]-x[1]*x[2])/(x[3]-x[1]-m*(x[2]-x[1]))
}
my.doubleratio.seq <- function(x,m,n=10000,both=TRUE){	
	ret <- rep(0,n)
	ret[1:3] <- x
	ret2 <- c()
	for(i in 4:n){
		ret[i] <- my.doubleratio.next(ret[(i-3):(i-1)],m)
	}
	if(both){
		ret2 <- my.doubleratio.seq(x[3:1],m,n=n,both=FALSE)
		return(c(ret2[n:4],ret))
	}else{
		return(ret)
	}
	
}

dd <- my.doubleratio.seq(x[1:3],median(my.doubleratio(x)),n=100)
plot(x,ylim=range(dd)+c(-1,1))
abline(h=range(dd),col=2)

XL <- c(min(dd),1)
XU <- c(max(dd),1)

V <- c(max(dd),1)/3

my.cross <- function(a,b,A,B){
	t <- ((b[1]-A[1])*(B[2]-A[2])-(b[2]-A[2])*(B[1]-A[1]))/((b[2]-A[2])*(a[1]-B[1])-(b[1]-A[1])*(a[2]-B[2]))
	t*a + (1-t)*A
}
a.lines <- b.lines <- rep(0,length(x)-1)
Ks <- matrix(0,length(x)-1,2)
for(i in 1:(length(x)-1)){
Ks[i,] <- my.cross(c(x[i],1),c(x[i+1],1),c(0,0),V)
a.line <- (Ks[i,2]-XL[2])/(Ks[i,1]-XL[1])
b.line <- 1 - XL[1] * a.line
a.lines[i] <- a.line
b.lines[i] <- b.line
}

points <- cbind(x,rep(1,length(x)))
points <- rbind(points,Ks)
points <- rbind(points,c(0,0))
points <- rbind(points,XL)
points <- rbind(points,XU)
points <- rbind(points,V)

plot(points,pch=20,col=c(rep(1,length(x)),rep(4,length(x)-1),2,rep(3,3)))
abline(h=1)
abline(0,1/XL[1])
abline(0,1/XU[1])
abline(b.lines[1],a.lines[1])