模様のできるわけ

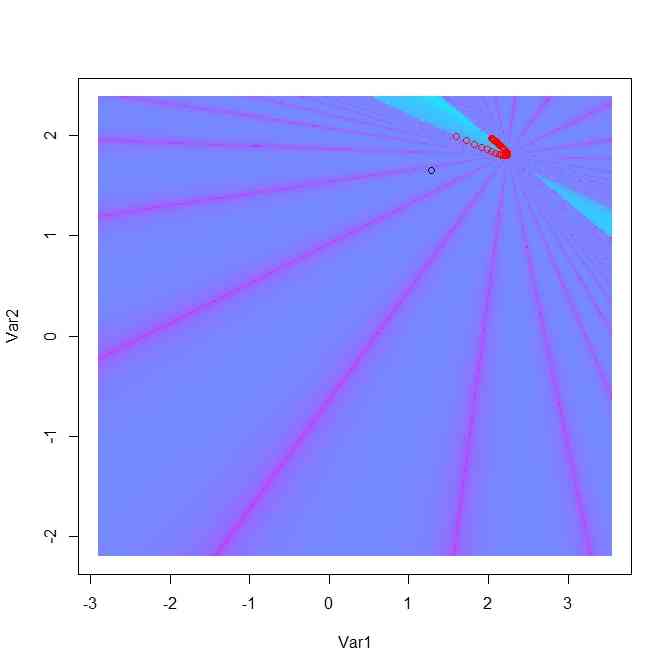
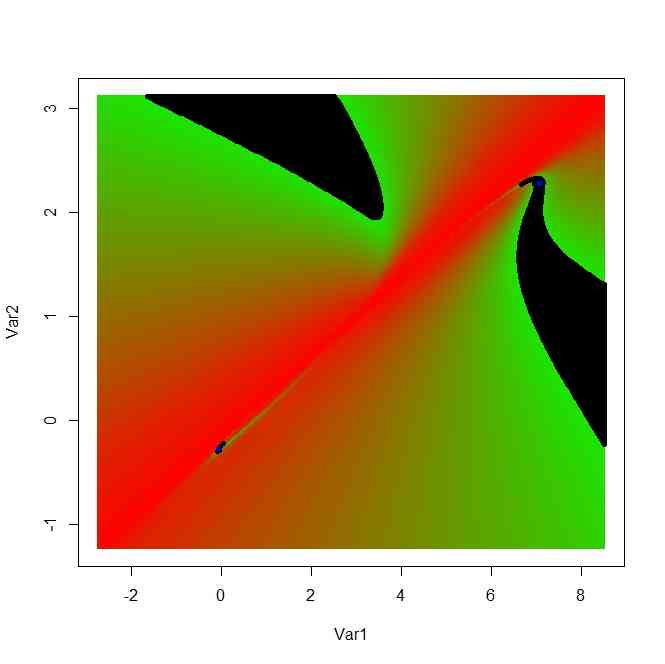
• 射影幾何、複比をいじっていたら、こんな模様ができた。
• どうしてこういう放射状の周期模様になるのか考え中…
• 考え中だけれど、とにかく面白い模様なのでひとまずコードをメモ(ランダム発生させているので、放射状波状模様になるとは限らないらしい…)

my.projection.simplex.edge <- function(x,z){
	d <- length(z[,1])
	coef.list <- coef.list.st <- bary.list <- list()
	xs.map <- xs.map2 <- matrix(0,d,d)
	xs.map[1,] <- xs.map2[1,] <- x
	coef.list[[1]] <- coef.list.st[[1]] <- c()
	for(i in 2:(d)){
		d. <- d-i+2
		zero <- z[,d.+1]
		tmp.z <- z[1:d.,1:d.]
		tmp.z.2 <- tmp.z - zero[1:d.]
		tmp.x <- xs.map[i-1,1:d.] - zero[1:d.]
		coef.list[[i]] <- solve(tmp.z.2) %*% tmp.x
		bary.list[[i]] <- c(coef.list[[i]],1-sum(coef.list[[i]]))
		coef.list.st[[i]] <- coef.list[[i]]/sum(coef.list[[i]])
		xs.map[i,] <- (z[,1:d.]-zero) %*% coef.list.st[[i]] + zero
		xs.map2[i,] <- z[,1:(d.+1)] %*% bary.list[[i]]
	}
	return(list(xs.map=xs.map,xs.map2=xs.map2,coef.list=coef.list,coef.list.st=coef.list.st,bary.list = bary.list))
}
exp.m <- function(A,n){
  # 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	#B <- diag(eigen.out[[1]]^n)
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}

my.doubleratio <- function(x){
	if(!is.matrix(x)){
		x <- matrix(x,nrow=length(x))
	}
	P <- x[1:(length(x[,1])-3),]
	Q <- x[4:length(x[,1]),]
	S <- x[2:(length(x[,1])-2),]
	R <- x[3:(length(x[,1])-1),]
	((P-R)/(Q-R))/((P-S)/(Q-S))
}
my.simplex.projection.crossratio <- function(Xs,Zs){
	d <- length(Xs[1,])
	ed <- combn(1:(d+1),2)
	ys <- matrix(0,length(Xs[,1]),length(ed[1,]))

	for(i in 1:length(Xs[,1])){
		for(j in 1:length(ed[1,])){
			tmp.Zs <- Zs[,c(ed[,j],(1:(d+1))[-ed[,j]])]
		tmp <- my.projection.simplex.edge(Xs[i,],tmp.Zs)
		coef.list.st <- tmp$coef.list.st
		ys[i,j] <- coef.list.st[[length(coef.list.st)]][1]
		}
	}
	my.doubleratio(ys)
}

calc.marg <- function(A){
  d <- dim(A)
  ret <- list()
  for(i in 1:length(d)){
    ret[[i]] <- apply(A,i,sum)
  }
  ret
}
# Expected table
#' Make an expected table
#'
#' @param A an array or matrix
#' @return The expected table in a shape of array or matrix
#' @examples
#' r <- c(2,3,4)
#' A <- array(1:prod(r),r)
#' make.exp.table(A)
make.exp.table <- function(A){
  n <- sum(A)
  marg <- calc.marg(A)
  tmp <- marg[[1]]
  for(i in 2:length(marg)){
    tmp <- t(marg[[i]]/n) %x% tmp
  }
  tmp
}
# Difference table
#' Make a table, the given table minus its expected table
#'
#' @param A an array or matrix
#' @return The difference table in a shape of array or matrix
#' @examples
#' r <- c(2,3,4)
#' A <- array(1:prod(r),r)
#' make.diff.table(A)
make.diff.table <- function(A){
  E <- make.exp.table(A)
  array(c(A)-c(E),dim(A))
}
# Chisquare value
#' Calculate chi-square value of an array or matrix
#'
#' @param A an array or matrix
#' @return The chi-square value of the table
#' @examples
#' r <- c(2,3,4)
#' A <- array(1:prod(r),r)
#' calc.chisq(A)
calc.chisq <- function(A){
  E <- make.exp.table(A)
  D <- make.diff.table(A)
  sum(c(D)^2/c(E))
}
# Simplex and rotation of simplex
# (d-1)-simplex is an polytope with d vertices in d-dimensional space
# This function gives coordinates of d vertices in d-1 dimensional space
#' Coordinate of simplex vertices
#'
#' @param d Number of vertices of a simplex
#' @return d times (d-1) matrix, each row of which is a coordinate of a vertex of (d-1)-simplex, whose center is the origin and distance of whose vertices from the origin is 1
#' @examples
#' d <- 3
#' cv <- CategoryVector(d)
#' print(cv)
#' apply(cv^2,1,sum)
#' cv %*% t(cv) 
CategoryVector<-function(d){
  df <- d - 1
  diagval <- 1:d
  diagval <- sqrt((d)/df) * sqrt((d - diagval)/(d - diagval + 1))
  others <- -diagval/(d - (1:d))
  m <- matrix(rep(others, d), nrow = d, byrow = TRUE)
  diag(m) <- diagval
  m[upper.tri(m)] <- 0
  as.matrix(m[, 1:df])
}

# This function gives coordinates of d vertices in "d" dimensional space with d-th coordinate of all vertices being equal and distance of all vertices from origin being 1.
# This is a rotation matrix.
# We call the output "simplex-rotation matrix".
#' Make a rotation matrix using simple vertices coordinates (1)
#'
#' @param k A integer
#' @return k x k rotation matrix to transfer k vertices so that all k vertices' k-th coordinates are the same
#' @examples
#' k <- 3
#' M <- make.simplex.0(k)
#' M %*% diag(rep(1,k))
make.simplex.0 <- function(k){
  cv <- CategoryVector(k)
  rbind(t(cv*sqrt(1-1/k)),rep(1/sqrt(k),k))
}

#' Make a rotation matrix using simple vertices coordinates (2)
#'
#' @param k A integer
#' @return k x k rotation matrix to transfer k vertices so that all k vertices' k-th coordinates are the same
#' @examples
#' k <- 3
#' M <- make.simplex(k)
#' M %*% diag(rep(1,k))
make.simplex <- function(k){
  ret <- matrix(0,k,k)
  for(i in 1:(k-1)){
    for(j in 1:k){
      if(j < i){
      }else if(j==i){
        ret[i,j] <-  sqrt((k-i)/(k-i+1))
      }else{
        ret[i,j] <- -sqrt(1/((k-i)*(k-i+1)))
      }
    }
  }
  ret[k,] <- sqrt(1/k)
  ret
}

simplex.crossratio <- function(X,k=10^10,n.replace=100,n.max=10000){
	d <- length(X[1,])
	max.x <- apply(X,2,max)
	min.x <- apply(X,2,min)
	ctr <- (max.x+min.x)/2
	X.st <- t(t(X)-ctr)
	max.x.st <- apply(X.st,2,max)
	min.x.st <- apply(X.st,2,min)
	max.r <- max(sqrt(apply(X.st^2,1,sum)))
	X.st.2 <- X.st/max.r
	min.R <- d
	cv <- CategoryVector(d+1)
	init <- cv * min.R * k
	curr <- init
	loop <- TRUE
	hx.v <- c()
	hx.cv <- matrix(0,0,length(cv))
	hx.cv <- rbind(hx.cv,c(t(t(matrix(curr,d+1,d) * max.r) + ctr)))
	tmp <- my.simplex.projection.crossratio(X.st.2,t(curr))
	#tmp2 <- apply(tmp,1,diff)
	tmp3 <- sum(apply(tmp,2,var))
	hx.v <- c(hx.v,tmp3)
	cnt <- 0
	cnt2 <- 0
	while(loop){
		cnt2 <- cnt2+1
		s <- sample(1:(d+1),1)
		new <- curr
		new[s,] <- new[s,] + rnorm(d)*runif(1)*10
		new[s,] <- new[s,] + rnorm(d)
		tmp <- my.simplex.projection.crossratio(X.st.2,t(new))
		tmp3 <- sum(apply(tmp,2,var))

		#tmp2 <- apply(tmp,2,diff)
		#tmp3 <- sum(tmp2^2)
		if(tmp3 < hx.v[length(hx.v)]){
			curr <- new
			curr2 <- t(t(matrix(curr,d,d+1) * max.r) + ctr)
			hx.cv <- rbind(hx.cv,c(curr2))
			hx.v <- c(hx.v,tmp3)
			cnt <- cnt + 1
		}
		if(cnt > n.replace){
			loop <- FALSE
		}
		if(cnt2 > n.max){
			loop <- FALSE
		}
	}
	return(list(hx.cv,hx.v,crossratio=tmp,no.replace=cnt,no.iter=cnt2))
}

d <- 2

library(GPArotation)
R <- Random.Start(d+1)
lambdas <- runif(d+1)
A <- R %*% diag(lambdas) %*% t(R)

#A <- matrix(rnorm((d+1)^2),d+1,d+1)
eigen.out <- eigen(A)
S <- (eigen.out[[2]])
S. <- t(t(S)/S[d+1,])
library(MCMCpack)
coef.init <- rdirichlet(1,rep(1,d+1))
X.init <- rep(0,d+1)
for(i in 1:(d+1)){
	X.init <- X.init + coef.init[i] * S.[,i]
}
t <- seq(from=-3,to=3,length=50)
X <- matrix(0,length(t),length(A[,1]))
for(i in 1:length(t)){
	X[i,] <- Re(exp.m(A,t[i])[[1]] %*% X.init)
}

X. <- X/X[,d+1]
cr <- my.simplex.projection.crossratio(X.[,1:2],S.[1:2,])
scr.out <- simplex.crossratio(X.[,1:2],k=3,n.replace=10,n.max=10)

XX <- matrix(0,0,d)
for(i in 1:(d+1)){
	XX <- rbind(XX,cbind(scr.out[[1]][,1+(i-1)*2],scr.out[[1]][,i*2]))
}
xlim <- ylim <- c(min(XX),max(XX))
par(mfcol=c(2,2))
plot(t(S.[1:2,]),col=2,pch=20,cex=0.5,xlim=xlim,ylim=ylim)
#plot(XX)
#points(t(S.[1:2,]),col=2)
col <- gray((scr.out[[2]]-min(scr.out[[2]]))/(max(scr.out[[2]])-min(scr.out[[2]])))
for(i in 1:length(scr.out[[1]][,1])){
	polygon(scr.out[[1]][i,1:3],scr.out[[1]][i,4:6],col=col)
}
points(t(S.[1:2,]),col=2,pch=20,cex=0.5)
points(X.[,1:2],col=3,pch=20,cex=0.5)

plot(scr.out[[2]])
matplot(scr.out[[3]],type="l")
matplot(scr.out[[1]],type="l")
par(mfcol=c(1,1))


my.2D.crossratio <- function(X,x){
	ret <- x[1]-(X[,1]-x[1])*x[2]/(X[,2]-x[2])
	return(ret)
}

XX <- X[,1:2]+2
min.XX <- apply(XX,2,min)
max.XX <- apply(XX,2,max)
diff.XX <- max.XX-min.XX
x <- seq(from=-min.XX[1]-diff.XX[1]*2,to=max.XX[1]+diff.XX[1]*2,length=300)
y <- seq(from=-min.XX[2]-diff.XX[2]*2,to=max.XX[2]+diff.XX[2]*2,length=300)

xy <- expand.grid(x,y)

p <- rep(0,length(xy[,1]))
for(i in 1:length(p)){
	tmp.xy <- unlist(xy[i,])
	tmp <- my.2D.crossratio(XX,tmp.xy)
	tmp2 <- my.doubleratio(tmp)
	p[i] <- var(tmp2)
}
tmp.col <- (log(p)-min(log(p)))/(max(log(p))-min(log(p)))
col <- rgb(tmp.col,1-tmp.col,1)
plot(xy,col=(log(p)==min(log(p))),pch=20,cex=0.2)
plot(xy,col=col,pch=20,cex=0.2)
points(XX,col=2)
points(xy,col=(log(p)==min(log(p))))
image(x,y,matrix(tmp.col,length(x),length(y)))
points(XX,col=1)
points(t(S.[1:2,]+2))
abline(h=0)
contour(x,y,matrix(tmp.col,length(x),length(y)),add=TRUE

• ちょっと改変

my.projection.simplex.edge <- function(x,z){
	d <- length(z[,1])
	coef.list <- coef.list.st <- bary.list <- list()
	xs.map <- xs.map2 <- matrix(0,d,d)
	xs.map[1,] <- xs.map2[1,] <- x
	coef.list[[1]] <- coef.list.st[[1]] <- c()
	for(i in 2:(d)){
		d. <- d-i+2
		zero <- z[,d.+1]
		tmp.z <- z[1:d.,1:d.]
		tmp.z.2 <- tmp.z - zero[1:d.]
		tmp.x <- xs.map[i-1,1:d.] - zero[1:d.]
		coef.list[[i]] <- solve(tmp.z.2) %*% tmp.x
		bary.list[[i]] <- c(coef.list[[i]],1-sum(coef.list[[i]]))
		coef.list.st[[i]] <- coef.list[[i]]/sum(coef.list[[i]])
		xs.map[i,] <- (z[,1:d.]-zero) %*% coef.list.st[[i]] + zero
		xs.map2[i,] <- z[,1:(d.+1)] %*% bary.list[[i]]
	}
	return(list(xs.map=xs.map,xs.map2=xs.map2,coef.list=coef.list,coef.list.st=coef.list.st,bary.list = bary.list))
}
exp.m <- function(A,n){
  # 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	#B <- diag(eigen.out[[1]]^n)
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}

my.doubleratio <- function(x){
	if(!is.matrix(x)){
		x <- matrix(x,nrow=length(x))
	}
	P <- x[1:(length(x[,1])-3),]
	Q <- x[4:length(x[,1]),]
	S <- x[2:(length(x[,1])-2),]
	R <- x[3:(length(x[,1])-1),]
	((P-R)/(Q-R))/((P-S)/(Q-S))
}
my.simplex.projection.crossratio <- function(Xs,Zs){
	d <- length(Xs[1,])
	ed <- combn(1:(d+1),2)
	ys <- matrix(0,length(Xs[,1]),length(ed[1,]))

	for(i in 1:length(Xs[,1])){
		for(j in 1:length(ed[1,])){
			tmp.Zs <- Zs[,c(ed[,j],(1:(d+1))[-ed[,j]])]
		tmp <- my.projection.simplex.edge(Xs[i,],tmp.Zs)
		coef.list.st <- tmp$coef.list.st
		ys[i,j] <- coef.list.st[[length(coef.list.st)]][1]
		}
	}
	my.doubleratio(ys)
}

calc.marg <- function(A){
  d <- dim(A)
  ret <- list()
  for(i in 1:length(d)){
    ret[[i]] <- apply(A,i,sum)
  }
  ret
}
# Expected table
#' Make an expected table
#'
#' @param A an array or matrix
#' @return The expected table in a shape of array or matrix
#' @examples
#' r <- c(2,3,4)
#' A <- array(1:prod(r),r)
#' make.exp.table(A)
make.exp.table <- function(A){
  n <- sum(A)
  marg <- calc.marg(A)
  tmp <- marg[[1]]
  for(i in 2:length(marg)){
    tmp <- t(marg[[i]]/n) %x% tmp
  }
  tmp
}
# Difference table
#' Make a table, the given table minus its expected table
#'
#' @param A an array or matrix
#' @return The difference table in a shape of array or matrix
#' @examples
#' r <- c(2,3,4)
#' A <- array(1:prod(r),r)
#' make.diff.table(A)
make.diff.table <- function(A){
  E <- make.exp.table(A)
  array(c(A)-c(E),dim(A))
}
# Chisquare value
#' Calculate chi-square value of an array or matrix
#'
#' @param A an array or matrix
#' @return The chi-square value of the table
#' @examples
#' r <- c(2,3,4)
#' A <- array(1:prod(r),r)
#' calc.chisq(A)
calc.chisq <- function(A){
  E <- make.exp.table(A)
  D <- make.diff.table(A)
  sum(c(D)^2/c(E))
}
# Simplex and rotation of simplex
# (d-1)-simplex is an polytope with d vertices in d-dimensional space
# This function gives coordinates of d vertices in d-1 dimensional space
#' Coordinate of simplex vertices
#'
#' @param d Number of vertices of a simplex
#' @return d times (d-1) matrix, each row of which is a coordinate of a vertex of (d-1)-simplex, whose center is the origin and distance of whose vertices from the origin is 1
#' @examples
#' d <- 3
#' cv <- CategoryVector(d)
#' print(cv)
#' apply(cv^2,1,sum)
#' cv %*% t(cv) 
CategoryVector<-function(d){
  df <- d - 1
  diagval <- 1:d
  diagval <- sqrt((d)/df) * sqrt((d - diagval)/(d - diagval + 1))
  others <- -diagval/(d - (1:d))
  m <- matrix(rep(others, d), nrow = d, byrow = TRUE)
  diag(m) <- diagval
  m[upper.tri(m)] <- 0
  as.matrix(m[, 1:df])
}

# This function gives coordinates of d vertices in "d" dimensional space with d-th coordinate of all vertices being equal and distance of all vertices from origin being 1.
# This is a rotation matrix.
# We call the output "simplex-rotation matrix".
#' Make a rotation matrix using simple vertices coordinates (1)
#'
#' @param k A integer
#' @return k x k rotation matrix to transfer k vertices so that all k vertices' k-th coordinates are the same
#' @examples
#' k <- 3
#' M <- make.simplex.0(k)
#' M %*% diag(rep(1,k))
make.simplex.0 <- function(k){
  cv <- CategoryVector(k)
  rbind(t(cv*sqrt(1-1/k)),rep(1/sqrt(k),k))
}

#' Make a rotation matrix using simple vertices coordinates (2)
#'
#' @param k A integer
#' @return k x k rotation matrix to transfer k vertices so that all k vertices' k-th coordinates are the same
#' @examples
#' k <- 3
#' M <- make.simplex(k)
#' M %*% diag(rep(1,k))
make.simplex <- function(k){
  ret <- matrix(0,k,k)
  for(i in 1:(k-1)){
    for(j in 1:k){
      if(j < i){
      }else if(j==i){
        ret[i,j] <-  sqrt((k-i)/(k-i+1))
      }else{
        ret[i,j] <- -sqrt(1/((k-i)*(k-i+1)))
      }
    }
  }
  ret[k,] <- sqrt(1/k)
  ret
}

simplex.crossratio <- function(X,k=10^10,n.replace=100,n.max=10000){
	d <- length(X[1,])
	max.x <- apply(X,2,max)
	min.x <- apply(X,2,min)
	ctr <- (max.x+min.x)/2
	X.st <- t(t(X)-ctr)
	max.x.st <- apply(X.st,2,max)
	min.x.st <- apply(X.st,2,min)
	max.r <- max(sqrt(apply(X.st^2,1,sum)))
	X.st.2 <- X.st/max.r
	min.R <- d
	cv <- CategoryVector(d+1)
	init <- cv * min.R * k
	curr <- init
	loop <- TRUE
	hx.v <- c()
	hx.cv <- matrix(0,0,length(cv))
	hx.cv <- rbind(hx.cv,c(t(t(matrix(curr,d+1,d) * max.r) + ctr)))
	tmp <- my.simplex.projection.crossratio(X.st.2,t(curr))
	#tmp2 <- apply(tmp,1,diff)
	tmp3 <- sum(apply(tmp,2,var))
	hx.v <- c(hx.v,tmp3)
	cnt <- 0
	cnt2 <- 0
	while(loop){
		cnt2 <- cnt2+1
		s <- sample(1:(d+1),1)
		new <- curr
		new[s,] <- new[s,] + rnorm(d)*runif(1)*10
		new[s,] <- new[s,] + rnorm(d)
		tmp <- my.simplex.projection.crossratio(X.st.2,t(new))
		tmp3 <- sum(apply(tmp,2,var))

		#tmp2 <- apply(tmp,2,diff)
		#tmp3 <- sum(tmp2^2)
		if(tmp3 < hx.v[length(hx.v)]){
			curr <- new
			curr2 <- t(t(matrix(curr,d,d+1) * max.r) + ctr)
			hx.cv <- rbind(hx.cv,c(curr2))
			hx.v <- c(hx.v,tmp3)
			cnt <- cnt + 1
		}
		if(cnt > n.replace){
			loop <- FALSE
		}
		if(cnt2 > n.max){
			loop <- FALSE
		}
	}
	return(list(hx.cv,hx.v,crossratio=tmp,no.replace=cnt,no.iter=cnt2))
}

d <- 2

library(GPArotation)
R <- Random.Start(d+1)
lambdas <- runif(d+1)
A <- R %*% diag(lambdas) %*% t(R)

#A <- matrix(rnorm((d+1)^2),d+1,d+1)
eigen.out <- eigen(A)
S <- (eigen.out[[2]])
S. <- t(t(S)/S[d+1,])
library(MCMCpack)
coef.init <- rdirichlet(1,rep(1,d+1))
X.init <- rep(0,d+1)
for(i in 1:(d+1)){
	X.init <- X.init + coef.init[i] * S.[,i]
}
t <- seq(from=-3,to=3,length=50)
X <- matrix(0,length(t),length(A[,1]))
for(i in 1:length(t)){
	X[i,] <- Re(exp.m(A,t[i])[[1]] %*% X.init)
}

X. <- X/X[,d+1]
cr <- my.simplex.projection.crossratio(X.[,1:2],S.[1:2,])
scr.out <- simplex.crossratio(X.[,1:2],k=3,n.replace=10,n.max=10)

XX <- matrix(0,0,d)
for(i in 1:(d+1)){
	XX <- rbind(XX,cbind(scr.out[[1]][,1+(i-1)*2],scr.out[[1]][,i*2]))
}
xlim <- ylim <- c(min(XX),max(XX))
par(mfcol=c(2,2))
plot(t(S.[1:2,]),col=2,pch=20,cex=0.5,xlim=xlim,ylim=ylim)
#plot(XX)
#points(t(S.[1:2,]),col=2)
col <- gray((scr.out[[2]]-min(scr.out[[2]]))/(max(scr.out[[2]])-min(scr.out[[2]])))
for(i in 1:length(scr.out[[1]][,1])){
	polygon(scr.out[[1]][i,1:3],scr.out[[1]][i,4:6],col=col)
}
points(t(S.[1:2,]),col=2,pch=20,cex=0.5)
points(X.[,1:2],col=3,pch=20,cex=0.5)

plot(scr.out[[2]])
matplot(scr.out[[3]],type="l")
matplot(scr.out[[1]],type="l")
par(mfcol=c(1,1))


my.2D.crossratio <- function(X,x){
	ret <- x[1]-(X[,1]-x[1])*x[2]/(X[,2]-x[2])
	return(ret)
}

XX <- X.[,1:2]
min.XX <- apply(XX,2,min)
max.XX <- apply(XX,2,max)
diff.XX <- max.XX-min.XX
x <- seq(from=min.XX[1]-diff.XX[1]*2,to=max.XX[1]+diff.XX[1]*2,length=500)
y <- seq(from=min.XX[2]-diff.XX[2]*2,to=max.XX[2]+diff.XX[2]*2,length=500)

xy <- expand.grid(x,y)

p <- rep(0,length(xy[,1]))
for(i in 1:length(p)){
	tmp.xy <- unlist(xy[i,])
	tmp <- my.2D.crossratio(XX,tmp.xy)
	tmp2 <- my.doubleratio(tmp)
	p[i] <- var(tmp2)
}
tmp.col <- (log(p)-min(log(p)))/(max(log(p))-min(log(p)))
tmp.col <- rank(p)/length(p)
col <- rgb(tmp.col,1-tmp.col,0)
plot(xy,col=(log(p)==min(log(p))),pch=20,cex=0.2)
plot(xy,col=col,pch=20,cex=0.2)
points(XX,col=2)
points(xy,col=(log(p) == min(log(p))),pch=20,cex=3)
points(xy,col=(log(p) < quantile(log(p),0.1)),pch=20,cex=1)
points(t(S.[1:2,]),pch=20,col=4)

image(x,y,matrix(tmp.col,length(x),length(y)))
points(XX,col=1)
points(t(S.[1:2,]),pch=20,col=4)
abline(h=0)
contour(x,y,matrix(tmp.col,length(x),length(y)),add=TRUE)