3. Path Curves in One and Two Dimenstions その２ ぱらぱらめくる『The Vortex of Life』

• 昨日の記事で２次元平面に「栗」を描いた
• この記事はその続き
• 栗をパラメタライズして一般化する
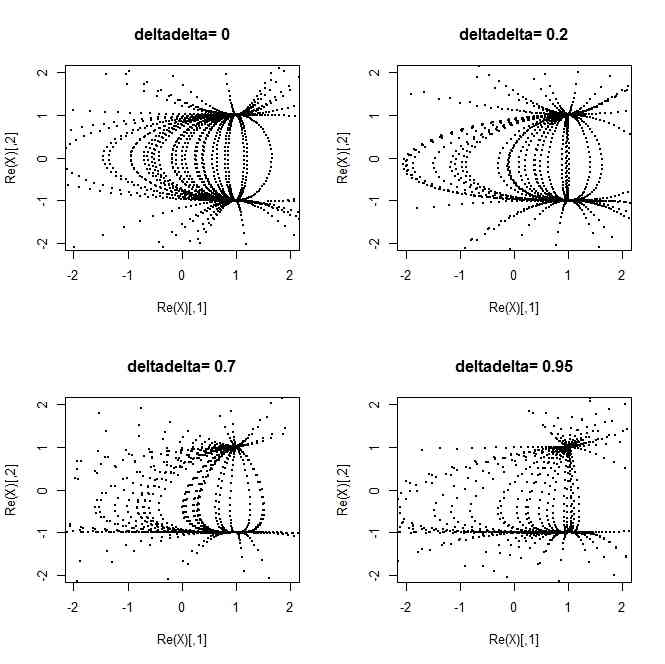
• ３つの固有値を(k3+D,k3+D+d,k3)とする
• 今、d=0のとき、栗の頭と尻は相互に対称になって、「楕円」になる
• dを小さい値にしておくと栗というより卵になる
  • d=0,0.2,0.7,0.95の場合

# 指数行列
exp.m <- function(A,n){
	# 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}
# d+1次元での連続軌道からd次元に戻す
my.pr.tr.cont <- function(x,M,t=seq(from=0,to=10,length=1000)){
	X <- c(x,1)
	out <- matrix(0,length(t),length(X))
	for(i in 1:length(t)){
		tmp <- exp.m(M,t[i])
		out[i,] <- tmp[[1]] %*% X
	}
	out2 <- out/out[,length(X)]
	out2[,-length(X)]
}

# 固有値
k3 <- 1
delta1 <- 0.5
deltadeltas <- c(0,0.2,0.7,0.95)
par(mfrow=c(2,2))
for(ii in 1:length(deltadeltas)){
	
deltadelta <- deltadeltas[ii]
delta2 <- -delta1 - deltadelta
ks <- c(k3+delta1,k3+delta2,k3)
# 固有ベクトル
vs <- matrix(c(1,-1,1,1,1,1,0.5,0,0),3,3)
Vs <- t(t(vs) * ks)
vs
Vs
R <- Vs %*% solve(vs)
R
eigen.out <- eigen(R)
eigen.out

n.iter <- 40
t <- seq(from=-10,to=10,length=100)
X <- matrix(0,0,2)
for(i in 1:n.iter){
	tmp <- rnorm(2)*1
	tmpX <- my.pr.tr.cont(tmp,R,t)
	X <- rbind(X,tmpX)
}
plot(Re(X),pch=20,cex=0.1,xlim=c(-2,2),ylim=c(-2,2),main=paste("deltadelta=",deltadelta))
}
par(mfrow=c(1,1))

• らせんは、不動点が１か所で、残りの２つは複素数座標

# 指数行列
exp.m <- function(A,n){
	# 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}
my.pr.tr.cont <- function(x,M,t=seq(from=0,to=10,length=1000)){
	X <- c(x,1)
	out <- matrix(0,length(t),length(X))
	for(i in 1:length(t)){
		tmp <- exp.m(M,t[i])
		out[i,] <- tmp[[1]] %*% X
	}
	out2 <- out/out[,length(X)]
	out2[,-length(X)]
}

x <- c(0.1,1)
theta <- runif(1)*2*pi
r <- 2
a <- cos(theta)*r
b <- sin(theta)*4
k <- 2
M <- matrix(c(a,b,0,-b,a,0,0,0,k),byrow=TRUE,3,3)

out <- my.pr.tr.cont(x,M,t=seq(from=0,to=10,length=1000))
plot(Re(out),type="l")

x <- c(0.1,1)

M <- diag(rnorm(3))

out <- my.pr.tr.cont(x,M,t=seq(from=0,to=10,length=1000))
plot(out,type="l")
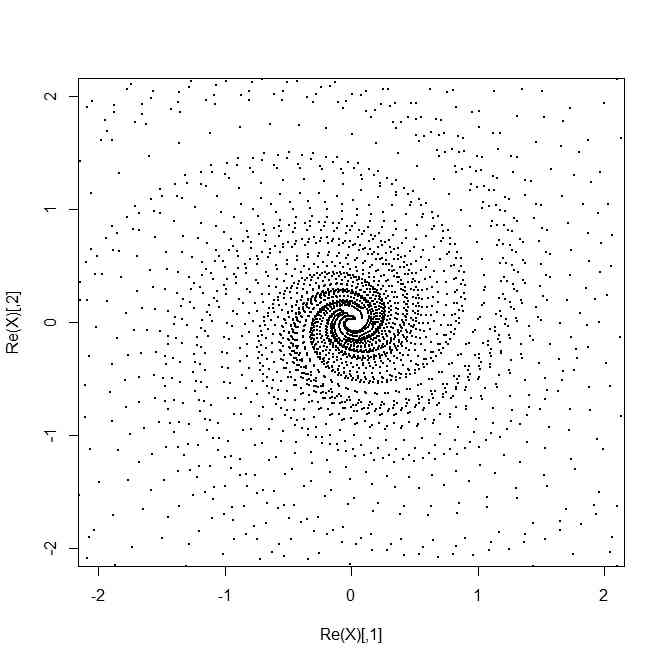
theta <- pi/5
R <- matrix(c(cos(theta),-sin(theta),0,sin(theta),cos(theta),0,0,0,1),3,3)

eigen(R)

n.iter <- 40
t <- seq(from=-10,to=10,length=100)
X <- matrix(0,0,2)
for(i in 1:n.iter){
	tmp <- rnorm(2)*1
	tmpX <- my.pr.tr.cont(tmp,R,t)
	X <- rbind(X,tmpX)
}
plot(Re(X),pch=20,cex=0.1,xlim=c(-2,2),ylim=c(-2,2))

par(mfrow=c(1,1))

• ３次元空間での回転軸を射影２次元平面に対して傾けると直線への収束も見えてくる

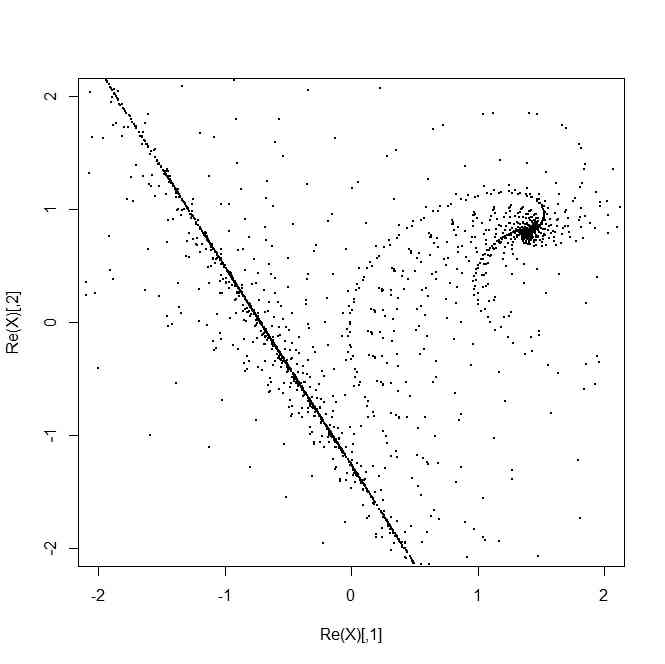
library(GPArotation)
theta <- pi/5
R <- matrix(c(cos(theta),-sin(theta),0,sin(theta),cos(theta),0,0,0,1),3,3)
R <- Random.Start(3) %*% R
eigen(R)

n.iter <- 40
t <- seq(from=-10,to=10,length=100)
X <- matrix(0,0,2)
for(i in 1:n.iter){
	tmp <- rnorm(2)*1
	tmpX <- my.pr.tr.cont(tmp,R,t)
	X <- rbind(X,tmpX)
}
plot(Re(X),pch=20,cex=0.1,xlim=c(-2,2),ylim=c(-2,2))

par(mfrow=c(1,1))