自然数は素数の対数の格子点 - ryamadaのコンピュータ・数学メモ

こちら(など)で素数とかリーマン予想とかゼータ関数についてごちゃごちゃと書いた
その中で、リーマンのゼータ関数の複素数０点の複素数部が作る数列に相当する櫛関数のフーリエ変換が素数とそのべき(素数べき)の対数での櫛関数になるという話を書いた
リーマンのゼータ関数と素数の関係はオイラー積表示にも表れるのだけれど、「素数べきの対数」ってどういうことなのか、と疑問に思う
素数の対数について考えてみる
すべての自然数の対数をとると、素数は $\log(n)$ と表すしかないけれど、 $x = y * z$ という自然数は $\log(x)=\log(y)+\log(z)$ なので、 $\log(y),\log(z)$ の線形和になっている
なので、Nまでのすべての自然数の対数は、N以下の素数の対数の線形和で表され、それは $\pi(N)$ (N以下の素数の個数)の次元で張った格子点として表せる、ということ
こちらに同様の記事
じゃあRを使ってその様子を見てみよう

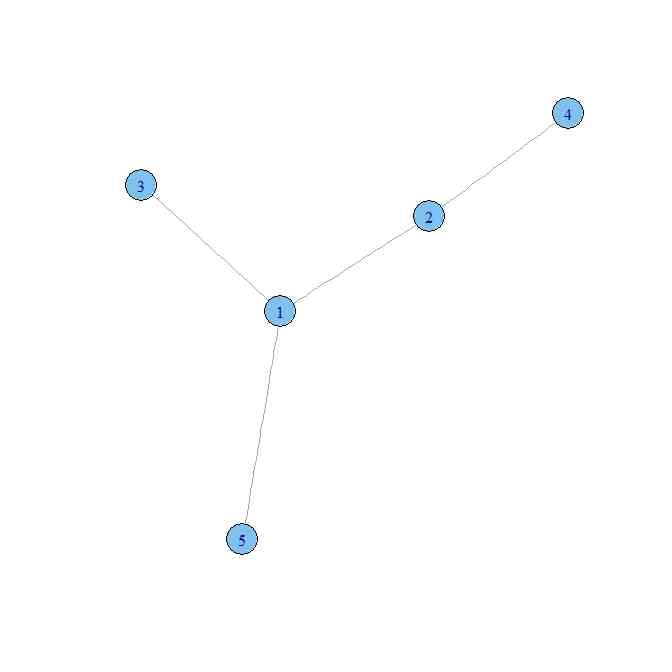
- この図はN=5のとき。1から2,3,5は直接、生えている、それは2,3,5が素数だから。4は2^2なので、2の方向に距離2の点
- 6に進めると、6=2*3なので、素数2,3の和になって四角形が現れる

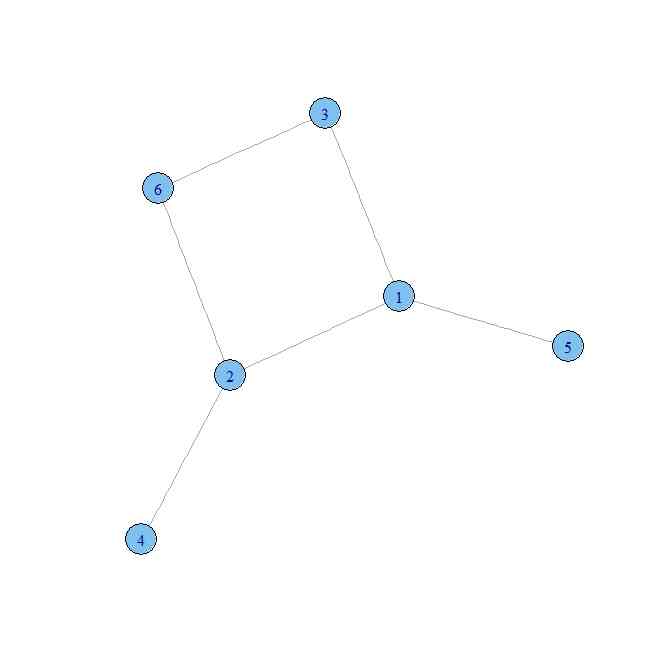
- これを1,2,3,4,5,6,7,8,9と順次進めると…

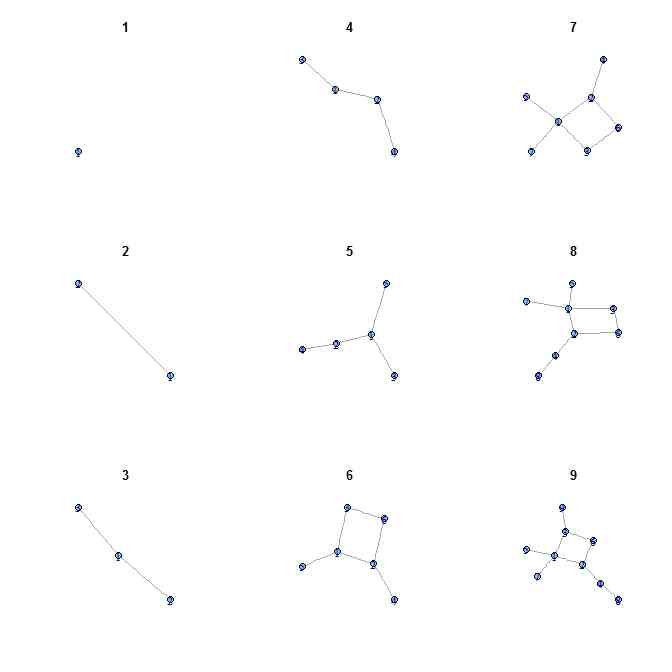
- N=200では？「カーブが現れる」。一番大きなカーブは素数２に対するもの、次に大きいカーブは素数３に対するもの、だろう・・・

今、素数の数(それは無限大なのだけれど)の次元の非負領域の超立方格子を考える。これは自然数全体に1対1対応する(ということで大丈夫だろうか…)
ここに $\sum_{i=1}^{\infty_{primes}} \frac{x_i}{\log{_{p_i} N}}=1$ なる平面を考える。ここで $\infty_{primes}$ とは素数の総数としての無限大なる数であり、 $p_i$ とは第i番目の素数とする
今Nを自然数とすると、この平面上ならびに平面より原点に近い側にはN個の格子点がある(格子点の座標は非負整数)
この平面が素数の数の軸をよぎるその座標が1以下である軸の数が、「自然数N以下の素数の総数」

library(numbers)
N <- 200
pri <- Primes(N)
X <- matrix(0,N,N)
# 各自然数を素因数分解してその結果を行列に納める
for(i in 2:N){
	X[i,] <- tabulate(factorize(i),N)
}
Y <- X[,pri]
# マンハッタン距離で自然数間の距離を定める
D <- as.matrix(dist(Y,method="manhattan"))
M <- matrix(as.numeric(D==1),N,N)
# グラフにする
library(igraph)

G <- graph.adjacency(M[1:5,1:5],mode="undirected")
plot(G)
G <- graph.adjacency(M[1:6,1:6],mode="undirected")
plot(G)

par(mfcol=c(3,3))

for(i in 1:9){
	G <- graph.adjacency(M[1:i,1:i],mode="undirected")
	plot(G,main=paste("",i))
}
par(mfcol=c(1,1))

G <- graph.adjacency(M,mode="undirected")
plot(G,layout=layout.circle(G))