- 問題はこちら
- □1
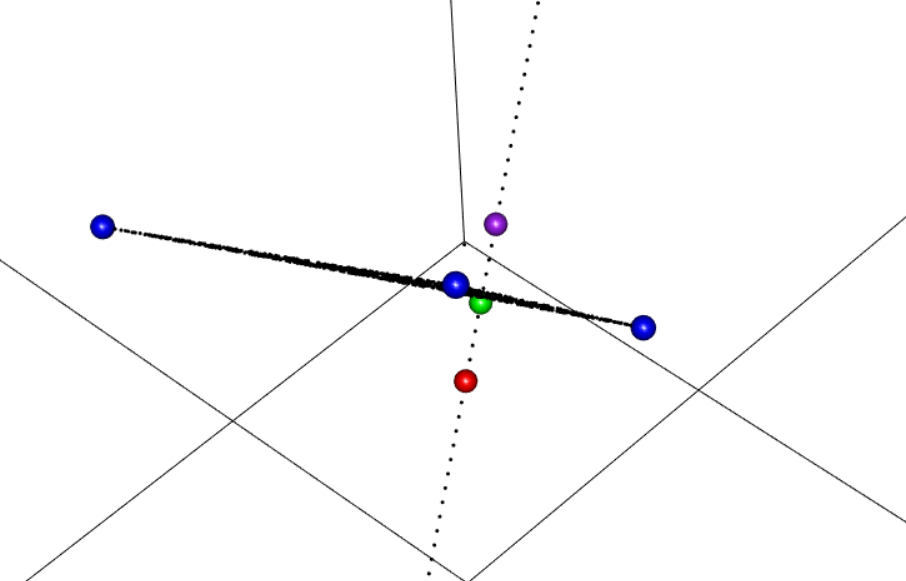
- 問1 3次元空間の3点が指定する平面に対称な点の座標を求める
- だいたいこのくらいの値
> Q
[1] 1.4444444 0.5555556 1.2222222
A <- c(1,0,0)
B <- c(0,-1,0)
C <- c(0,0,2)
AB <- B-A
AC <- C-A
n <- c(AB[2] * AC[3] - AB[3] * AC[2],AB[3] * AC[1] - AB[1] * AC[3], AB[1] * AC[2] - AB[2] * AC[1])
P <- c(1,1,1)
t <- seq(from=-3,to=3,length=100)
L <- matrix(0,length(t),3)
for(i in 1:length(L[,1])){
L[i,] <- P + t[i] * n/sqrt(sum(n^2))
}
library(rgl)
library(MCMCpack)
S <- as.matrix(rdirichlet(1000,c(1,1,1)))
X <- rbind(P,A,B,C,L,S %*% rbind(A,B,C))
rg <- range(X)
X <- rbind(X,rep(rg[1],3),rep(rg[2],3))
plot3d(X)
spheres3d(P,color="red",radius=0.05)
spheres3d(rbind(A,B,C),color="blue",radius=0.05)
tmp <- apply((t(L)-A)^2,2,sum)
selected <- which(tmp==min(tmp))
M <- L[selected,]
Q <- P + 2 * t[selected] * n/sqrt(sum(n^2))
spheres3d(M,color="green",radius=0.05)
spheres3d(Q,color="purple",radius=0.05)
Q
-
- 問2 4タイプの等確率サンプリングで、n回目に初めて特定のタイプが観察され、1-(n-1)回目までに残りの3タイプが1回以上観察される確率
- 乱択実験する
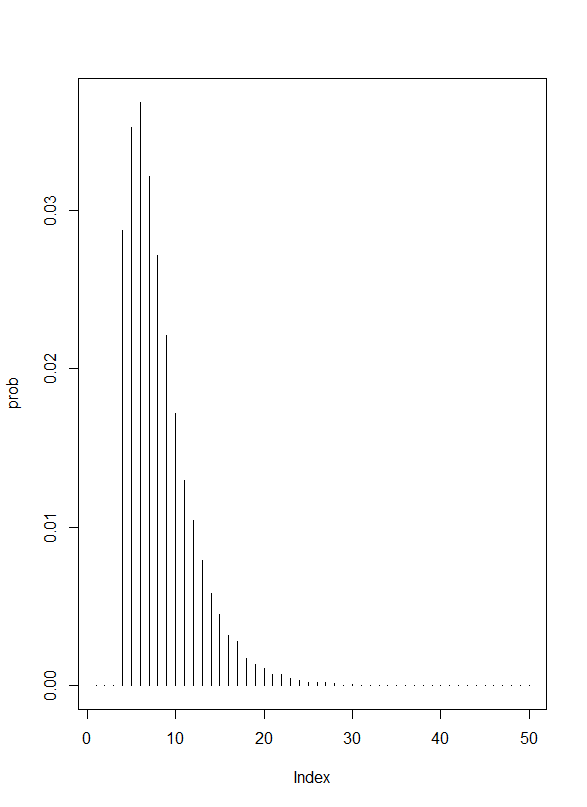
n.trial <- 10^5
n.events <- 50
X <- matrix(sample(1:4,n.trial*n.events,replace=TRUE),ncol=n.events)
prob <- rep(0,n.events)
for(i in 4:n.events){
tmp <- which(X[,i] == 1)
tmpX <- as.matrix(X[tmp,1:(i-1)],ncol=i-1)
tmp2 <- (apply(tmpX-2,1,prod) + apply(tmpX-3,1,prod) + apply(tmpX-4,1,prod)) == 0 & (apply(tmpX-1,1,prod) !=0)
prob[i] <- sum(tmp2)/n.trial
}
plot(prob,type="h")
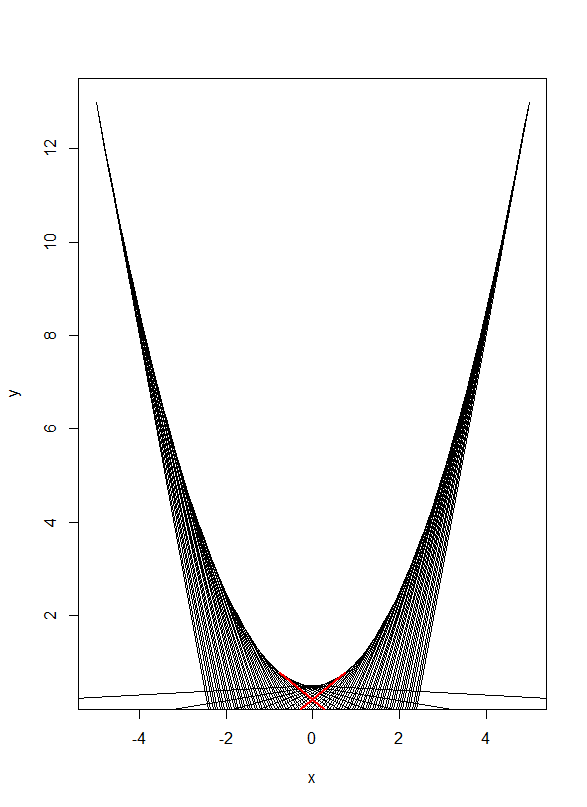
- □2 2次曲線
 上の点接線とx軸の交点距離の最小値
上の点接線とx軸の交点距離の最小値
x <- seq(from=-5,to=5,length=100)
y <- 1/2 * (x^2+1)
plot(x,y,type="l")
L <- rep(0,length(x))
for(i in 1:length(x)){
Qx <- x[i]-y[i]/x[i]
Qy <- 0
L[i] <- sqrt((x[i]-Qx)^2 + (y[i]-Qy)^2)
}
s <- which(L==min(L))
min(L)
plot(x,y,type="l")
for(i in 1:length(x)){
Qx <- x[i]-y[i]/x[i]
Qy <- 0
segments(x[i],y[i],x[i]-y[i]/x[i],0)
}
for(i in 1:length(s)){
Qx <- x[s[i]]-y[s[i]]/x[s[i]]
Qy <- 0
segments(x[s[i]],y[s[i]],x[s[i]]-y[s[i]]/x[s[i]],0,col="red",lwd = 2)
}
- □3
 の和
の和
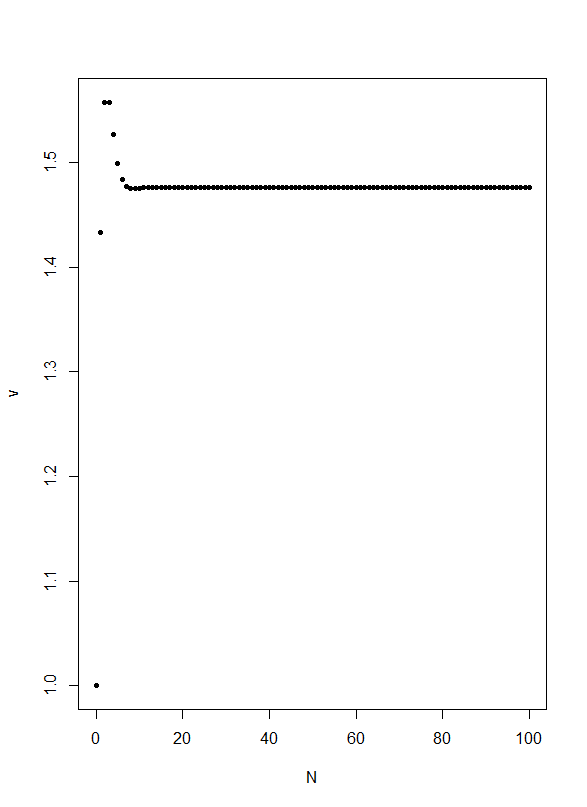
- 収束するなら計算機は得意
- だいたい 1.476627 (
 )
)
N <- 0:100
v <- rep(0,length(N))
for(i in 1:length(N)){
v[i] <- sum((1/2)^(0:N[i]) * cos((0:N[i])*pi/6))
}
plot(N,v,pch=20)
v[length(v)]
- □4
 の曲線の長さ
の曲線の長さ
- 細かく点列を作って、折れ線の長さを求めれば近似値は求まる
- 1.762747くらい (2log(sqrt(2)+1))
x <- seq(from=0,to=pi/2,length=10000)
y <- log(1+cos(x))
plot(x,y,type="l")
diff.x <- diff(x)
diff.y <- diff(y)
L <- sum(sqrt(diff(x)^2+diff(y)^2))
L
- □5
 の2点B,Cを底辺とした2等辺三角形の頂点がy軸上にあるとき、それは正三角形であるから、外心が原点で半径が2であるような三角形ABCについての問題である
の2点B,Cを底辺とした2等辺三角形の頂点がy軸上にあるとき、それは正三角形であるから、外心が原点で半径が2であるような三角形ABCについての問題である
- 原点中心の円周上に3点を持つ三角形の垂心座標は、(3点のx座標の和,3点のy座標の和)となることを使えば、以下のように、黒がAの座標で半径2の円周、緑と青で描かれれる円が、垂心座標であり、そのうち、青がAのy座標が正の場合
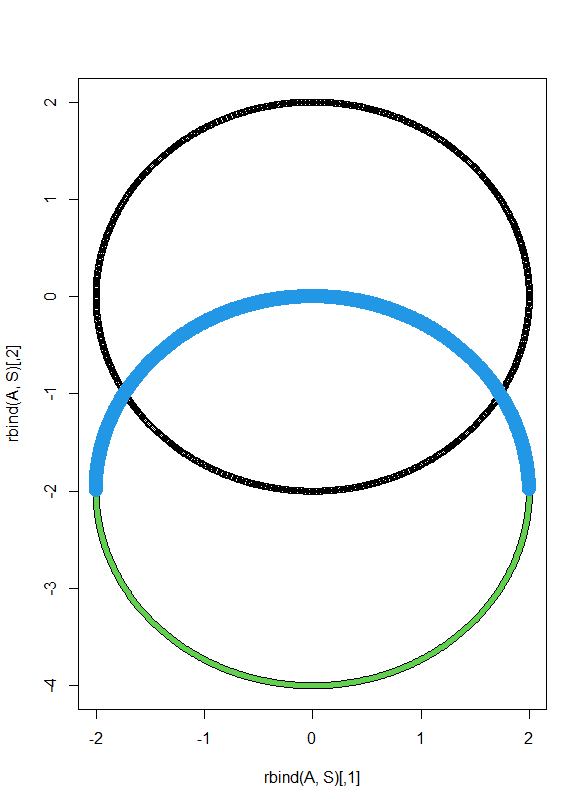
B <- c(-sqrt(3),-1)
C <- c(sqrt(3),-1)
t <- seq(from=0,to=1,length=1000) * 2 * pi
A <- cbind(2*cos(t),2*sin(t))
points(B[1],B[2],pch=20,col=2)
points(C[1],C[2],pch=20,col=2)
S <- cbind(A[,1]+B[1]+C[1], A[,2]+B[2]+C[2])
plot(rbind(A,S))
points(S,pch=20,col=3)
posi <- which(A[,2]>0)
points(S[posi,],pch=20,cex=3,col=4)
- □6
- 問1 素数。
 が素数なら 、nは素数
が素数なら 、nは素数
- 対偶。nが素数で内なら
 は素数ではない
は素数ではない
- いずれにしても、無限に大きい数に関して、ルールがはっきりしない素数に関する「証明問題」は単なる例示的計算機利用は苦手
library(primes)
n <- 2:10000
K <- 3^n - 2^n
p.or.notp.1 <- is_prime(K)
p.or.notp.2 <- is_prime(n)
table(p.or.notp.2[which(p.or.notp.1)])
table(p.or.notp.1[which(p.or.notp.2)])
table(p.or.notp.2[which(!p.or.notp.2)])
table(p.or.notp.2[which(!p.or.notp.1)])
-
- 問2 点(1,p) と 点(a, ap) (a > 1)とを通る微分可能な関数の接線の中に原点を通るものがあることを示す
- 2点を通り、一般性のある微分可能な関数を描いて見せて、原点を通る直線のなかに、接線になりそうなものがありそうなことを図示して、それっぽさを示すことにする
 という関数はg(x)が微分可能な時、確かに、(1,p)を通り、(a,ap)を通る
という関数はg(x)が微分可能な時、確かに、(1,p)を通り、(a,ap)を通る

p <- 1.3
a <- pi/2
g <- function(x){
sin(x^2) + 3 * x + 0.2 * x^2 - 0.004 * x^3 + 5
}
f <- function(x,p,a){
0.1 * (x-1) * (x-a) * g(x) + x * p
}
x <- seq(from=-3,to=3,length=100)
y <- f(x,p,a)
plot(x,y,type="l")
abline(v=1)
abline(v=a)
abline(h=p)
abline(h=p*a)
t <- seq(from=0,to=1,length=25) * 2 * pi
for(i in 1:length(t)){
abline(0,tan(t[i]),col=2)
}

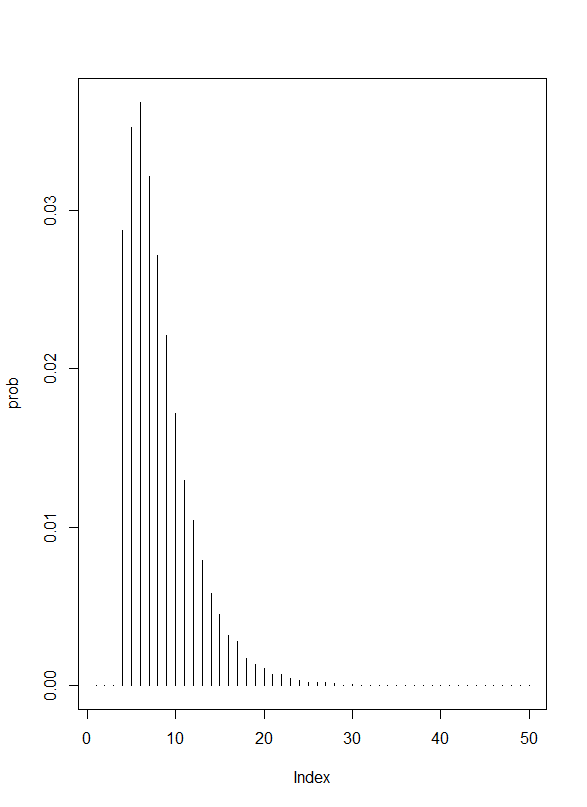
上の点接線とx軸の交点距離の最小値

の和
)

の曲線の長さ
の2点B,Cを底辺とした2等辺三角形の頂点がy軸上にあるとき、それは正三角形であるから、外心が原点で半径が2であるような三角形ABCについての問題である

