元に戻ってくる

• 回転行列による変化が続くとき、２次元の回転では、円を描いて、元に戻るけれど、３次元以上では、元に戻るとは限らない。ある大円では、周期t1で戻ってくるのに、別の大円では周期t2で戻ってきて、t1とt2とが「公倍数」を持たなければ、そうなるだろう
• 周期t1,t2が有理数なら、いつか必ず、元に戻るが、片方が無理数で、相互に公倍数を持たないときには、永遠に巡り会えない、回軌道になる
• そんなことをやってみるために、こんな回転行列を作ってみよう
  • きちんと元に戻ってくるような回転を(いくつか定める)
  • 戻ってくる回転の周期を決める
  • 回転をこのような回転の複合とする
• きちんと元に戻ってくるような回転の例
  • 置換行列はせいぜい回の繰り返しによって、元に戻る

> k<-3
> m<-diag(rep(1,k))
> m<-m[sample(1:k),]
> m
     [,1] [,2] [,3]
[1,]    0    0    1
[2,]    1    0    0
[3,]    0    1    0

• 戻ってくる周期を定める
  • 上のような置換行列に関して、単位時間あたり、有理数乗分の回転をさせることとする
  • 回転すると、置換行列と同じ回転ができるから、時間経てば、元に戻る
• これをやってわかったこと
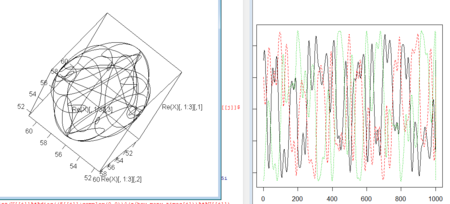
  • ３次元空間でこの作業をやると「２次元平面上」を移動するということ…

# 次元
k<-3
# 次元kの単位ベクトル
M<-diag(rep(1,k))
# 置換行列をいくつ作るか
n<-5
# 置換行列のリスト
T<-list()
for(i in 1:n){
	T[[i]]<-M[sample(1:k),]
}
# 各置換行列の単位時間当たりの回転程度を自然数で与える
how.many.times<-sample(2:10,n,replace=TRUE)

# 各置換行列の特異値分解の固有値と固有ベクトルを格納
S<-list()
V<-list()
U<-list()
for(i in 1:n){
	tmp<-T[[i]]
	e.out<-eigen(tmp)
	S[[i]]<-e.out$values
	V[[i]]<-e.out$vectors
	U[[i]]<-solve(V[[i]])
}
# すべての周期の公倍数であって、かつ、k!の倍数であるような時刻
# もとに戻るはずの時刻
z<-prod(how.many.times)*factorial(k)

# 連続的時刻と元に戻るはずの時刻のリスト
t<-seq(from=0,to=100,length=1000)
t<-c(t,z)
# 初期座標
x<-runif(k)*100
Niter<-length(t)
X<-matrix(0,Niter,k)
# 時刻ごとに座標を計算
for(i in 1:length(t)){
	tmpx<-x
	# 置換行列ごとに、指定時刻までの回転をさせ
	# すべての置換行列の処理を重ねる
	for(j in 1:n){
		tmpx<-V[[j]]%*%diag((S[[j]]+complex(0,0))^(t[i]/how.many.times[j]))%*%U[[j]]%*%tmpx
	}
	X[i,]<-tmpx
}
# plotする
matplot(Re(X),type="l")

library(rgl)
plot3d(Re(X)[,1:3],type="l")
# もとに戻っていることの確認
X[1,]-X[length(t),]

# 各置換行列が単位行列に戻っていることの確認
for(i in 1:n){
	print(V[[j]]%*%diag((S[[j]]+complex(0,0))^(z/how.many.times[j]))%*%U[[j]])
}