2012-04-16

折る

折り紙

こちらで、地図をくしゃくしゃに丸める話があった(こちらの関係)
折り紙と考える
まずは、折り紙の基本『3次元空間において、2次元平面を1次元の直線に関して谷折り』にしてみる

Clist<-list()
x1<-0.5
y1<-0
t1<-pi/4
p1<-pi/6
Clist[[1]]<-c(x1,y1,t1,p1)

# 元の平面の座標
x<-matrix(runif(10000*2)*2,ncol=2)
# 空間の座標
X<-c(x,0)

Ore<-function(crease,x){
	tmpx<-t(x)-crease[1:2]
	theta<-crease[3]
	phi<-crease[4]
	rot<-matrix(c(cos(theta),sin(theta),-sin(theta),cos(theta)),byrow=TRUE,ncol=2)
	rot2<-matrix(c(cos(theta),-sin(theta),sin(theta),cos(theta)),byrow=TRUE,ncol=2)
	tmpx2<-rot%*%tmpx
	ret<-matrix(0,length(x[,1]),3)
	ret<-rbind(tmpx2[1,],tmpx2[2,]*cos(phi/2),abs(tmpx2[2,])*sin(phi/2))
	tmpret<-rot2%*%(ret[1:2,])
	tmpret<-tmpret+crease[1:2]
	ret<-t(rbind((tmpret),ret[3,]))
	return(ret)
}

xout<-Ore(Clist[[1]],x)

library(rgl)
plot3d(xout)

道具を少し
- 垂線の足や正規直交基底を

# 3次元でxyを結ぶ直線へのzからの足の座標
ashi<-function(x,y,z){
	t<-sum((z-y)*(x-y))/sum((x-y)^2)
	x*t+(1-t)*y
}
# 3次元ベクトルxとzが作る平面の法線ベクトル
perpendic<-function(x,z){
	y<-rep(0,3)
	y[1]<-(x[2]*z[3]-x[3]*z[2])/sqrt((x[2]*z[3]-x[3]*z[2])^2+(x[3]*z[1]-x[1]*z[3])^2+(x[1]*z[2]-x[2]*z[1])^2)
	y[2]<-y[1]*(x[3]*z[1]-x[1]*z[3])/(x[2]*z[3]-x[3]*z[2])
	y[3]<--(x[1]*y[1]+x[2]*y[2])/x[3]
	return(y)
}

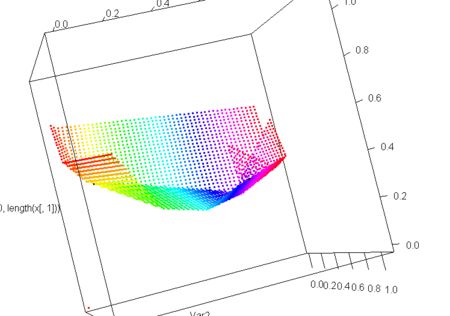
とにかく折ってみる
- まだ折り重なりが複数回になったりするところや、谷折りと山折りの区別とかがうまくないけれど…

# 垂線の足座標
ashi<-function(x,y,z){
	t<-sum((z-y)*(x-y))/sum((x-y)^2)
	x*t+(1-t)*y
}
# 法線ベクトル
perpendic<-function(x,z){
	y<-rep(0,3)
	if(x[3]==z[3]){
		return(c(0,0,1))
	}
	if(x[3]==0){
		tmpx<-x
		tmpz<-z
		x<-z
		z<-tmpx
	}
	y[1]<-(x[2]*z[3]-x[3]*z[2])/sqrt((x[2]*z[3]-x[3]*z[2])^2+(x[3]*z[1]-x[1]*z[3])^2+(x[1]*z[2]-x[2]*z[1])^2)
	y[2]<-y[1]*(x[3]*z[1]-x[1]*z[3])/(x[2]*z[3]-x[3]*z[2])
	y[3]<--(x[1]*y[1]+x[2]*y[2])/x[3]
	return(y)

}
# cr1 cr2を結ぶ直線で角pで折るときにxが移動する先の座標
Oru.one<-function(x,cr1,cr2,p){
	ashi.x<-c(ashi(cr1,cr2,x))
	tmpx<-x-ashi.x
	tmpz<-cr2-ashi.x
	tmpx2<-tmpx/sqrt(sum(tmpx^2))
	tmpz2<-tmpz/sqrt(sum(tmpz^2))
	tmpy2<-perpendic(tmpx2,tmpz2)
	tmpy2<-tmpy2*sign(tmpy2[3])
	rot<-cbind(tmpx2,tmpy2,tmpz2)
	#rot<-abs(rot)
	ret<-c(cos(p),sin(p),0)*sqrt(sum(tmpx^2))
	ret2<-rot%*%ret
	ret3<-ret2+ashi.x
	return(ret3)	
}
# xy平面上の点の集合xをその面上での２点cr1からcr2への直線を折れ線として
# 折った後角度がpになるようにおりたい
# x,cr1,cr2は元の平面座標
# X, Cr1, Cr2は折りすすめたときの３次元座標jはcr1,cr2の第j行の座標を折れ線を決める２点の座標とすることを示すもの
# 返り値はj回折った後の、cr1,cr2,xの３次元空間座標
Oru<-function(cr1,cr2,p,j,x,X,Cr1,Cr2){
	retX<-X
	retCr1<-Cr1
	retCr2<-Cr2
	for(i in 1:length(retX[,1])){
		retX[i,]<-Oru.one(X[i,],Cr1[j,],Cr2[j,],p[j]/2)
	}
	for(i in 1:length(retCr1[,1])){
		if(i!=j){
			retCr1[i,]<-Oru.one(Cr1[i,],Cr1[j,],Cr2[j,],p[j]/2)
			retCr2[i,]<-Oru.one(Cr2[i,],Cr1[j,],Cr2[j,],p[j]/2)
		}
	}
	return(list(X=retX,Cr1=retCr1,Cr2=retCr2))
}

k<-3
# 平面格子点
L<-seq(from=0,to=1,length=50)
x<-expand.grid(L,L)
# 折るための2点をNcペア作る
Nc<-10
cr1<-matrix(runif(Nc*2),Nc,2)
cr2<-cr1+matrix(rnorm(Nc*2),Nc,2)*0.0001
# 折って作る角度
p<-runif(Nc)*pi/5
#p<-rep(pi/1,Nc)
#p<-rep(pi/(Nc*2),Nc)
X<-list()
X[[1]]<-as.matrix(cbind(x,rep(0,length(x[,1]))))
Cr1<-Cr2<-list()
Cr1[[1]]<-as.matrix(cbind(cr1,rep(0,Nc)))
Cr2[[1]]<-as.matrix(cbind(cr2,rep(0,Nc)))
for(i in 1:Nc){
	Ori.out<-Oru(cr1,cr2,p,i,x,X[[i]],Cr1[[i]],Cr2[[i]])
	X[[i+1]]<-Ori.out$X
	Cr1[[i+1]]<-Ori.out$Cr1
	Cr2[[i+1]]<-Ori.out$Cr2
}

library(rgl)
for(i in 1:(Nc+1)){
	plot3d(X[[i]],col=rainbow(length(x[,1])))
	Sys.sleep(0.3)
}
for(i in 1:(Nc+1)){
	mmin<-min(X[[i]])
	mmax<-max(X[[i]])
	minpt<-rep(mmin,3)
	maxpt<-rep(mmax,3)
	plot3d(rbind(X[[i]],Cr1[[i]],Cr2[[i]],minpt,maxpt),col=c(rainbow(length(x[,1])),rep(1,2*Nc),rep(2,2)))
	Sys.sleep(2)
}

谷折りの一般次元系
- n次元空間で折る
- n-1次元の「平らな」多様体を折る
- n-2次元の「平らな」多様体で折る
- n-1次元の「平らな」多様体から立ち上がるようにして折る
折り紙に翻訳すると
- 3次元空間で折る
- 2次元の平らな多様体(紙)を折る
- 1次元の平らな多様体(直線)で折る
- 2次元の平らな多様体(平面)から立ち上がるようにして折る
こちらに関連話題