- 要素数nの集合の部分集合の族は
 個の部分集合からなり、それらの包含関係は超立方体の形をしたポセットになっている
個の部分集合からなり、それらの包含関係は超立方体の形をしたポセットになっている
- このポセットを無向グラフと見ると、n正則グラフになっている
- 見方を変える
- n本の紐を互いに1度ずつだけ交叉させて、紐の順序を1,2,3,...,nからn,n-1,...,2,1にするようなn本の紐の配置をすることとする
- 紐の両端には閉じていない部屋が(n-1)個ずつ、併せて2(n-1)できる(一番下と一番上は数えない)
- 紐で閉じた部屋は
 個できる
個できる
- 閉じた部屋も閉じない部屋も、その部屋の下にある紐の番号の集合でID付けをすることにする
- このn本の紐が作る部屋のパターンにつき次のルールで矢印をつける
- 同じ段にあるときは、左から右に矢印をつける
- 左斜め下、左斜め上にある部屋に矢印をつける
- 両端にある閉じていない部屋の間には矢印をつけない
- この有向グラフを箙と見ると、閉じた部屋が変異可能頂点、閉じていない部屋が変異できない頂点とした、団代数になるという
- また、この団変異によって、すべての部分集合が現れるという
- この団代数では、2(n-1)個のfrozen な頂点~変異できない頂点があり、
 個の変異可能な頂点ができるので、拡大skew-symmetric 行列が作れる。
個の変異可能な頂点ができるので、拡大skew-symmetric 行列が作れる。 列で
列で 行の行列
行の行列
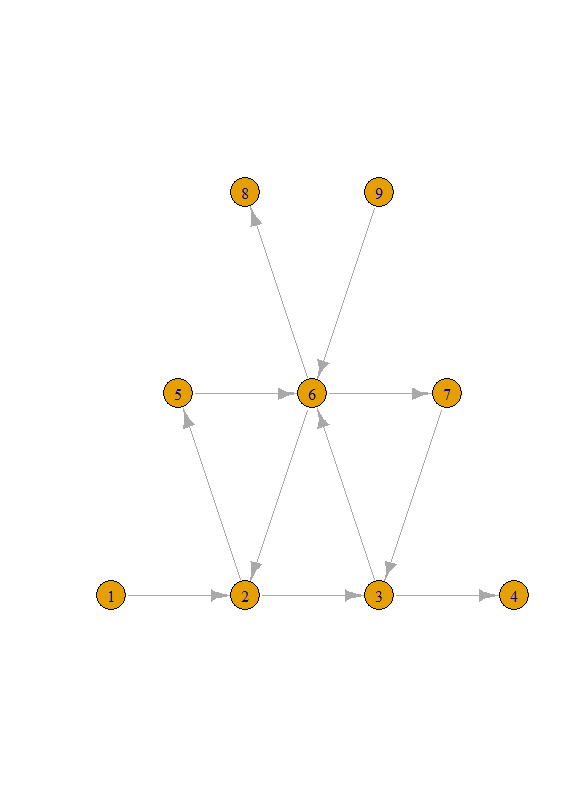
- 2,3,6の頂点がmutable、それ以外がfrozen
- 以下の行列では、1,2,3行、1,2,3列が、頂点番号2,3,6に相当
- 4,5,6,7,8,9行が、頂点番号1,4,5,7,8,9に相当
- この変異により、flag minor ({2,4,5}が選ばれたときには、全体の行列の2,4,5行と1,2,3列とを抜き出した正方行列を考え、その行列式のこと)に関して、トレミーの定理が成り立つことから、すべてのflag minorsが正であることの判定が、
 個のflag minorsの正の確認で済むことが導ける
個のflag minorsの正の確認で済むことが導ける
> out$B.ext
[,1] [,2] [,3]
[1,] 0 1 -1
[2,] -1 0 1
[3,] 1 -1 0
[4,] 1 0 0
[5,] 0 -1 0
[6,] -1 0 1
[7,] 0 1 -1
[8,] 0 0 -1
[9,] 0 0 1
> my.B.mut(out$B.ext,2)
[,1] [,2] [,3]
[1,] 0 -1 0
[2,] 1 0 -1
[3,] 0 1 0
[4,] 1 0 0
[5,] -1 1 0
[6,] -1 0 1
[7,] 0 -1 0
[8,] 0 0 -1
[9,] 0 0 1
my.B.flagminor <- function(n){
unbound.chamber <- 2 * (n-1)
bound.chamber <- (n-1) * (n-2) /2
total.chamber <- unbound.chamber + bound.chamber
B <- matrix(0,total.chamber,total.chamber)
n.chamber.per.row <- n:2
n.row <- n-1
id.first.row <- c(1,cumsum(n.chamber.per.row)[1:(n.row-1)]+1)
for(i in 1:(n.row-1)){
for(j in 1:(n.chamber.per.row[i]-1)){
tmp <- id.first.row[i] + j -1
tmp2 <- tmp + 1
B[tmp,tmp2] <- 1
}
}
for(i in 1:(n.row-1)){
for(j in 2:(n.chamber.per.row[i]-1)){
tmp <- id.first.row[i] + j -1
tmp2 <- id.first.row[i+1] + (j-1) -1
B[tmp,tmp2] <- 1
}
}
for(i in 2:n.row){
for(j in 2:n.chamber.per.row[i]){
tmp <- id.first.row[i] + j -1
tmp2 <- id.first.row[i-1] + j -1
B[tmp,tmp2] <- 1
}
}
frozen <- c()
for(i in 1:(n.row-1)){
frozen <- c(frozen,id.first.row[i],id.first.row[i+1]-1)
}
frozen <- c(frozen,id.first.row[n.row],id.first.row[n.row]+1)
mutable <- (1:length(B[,1])) [-frozen]
B. <- B[c(mutable,frozen),c(mutable,frozen)]
B.skew <- B. - t(B.)
B.ext <- B.skew[,1:length(mutable)]
return(list(B.ext = B.ext,B=B,B.skew=B.skew,B.=B.))
}
my.layout.flagminor <- function(n){
unbound.chamber <- 2 * (n-1)
bound.chamber <- (n-1) * (n-2) /2
total.chamber <- unbound.chamber + bound.chamber
n.chamber.per.row <- n:2
n.row <- n-1
id.first.row <- c(1,cumsum(n.chamber.per.row)[1:(n.row-1)]+1)
xy <- matrix(0,0,2)
for(i in 1:n.row){
tmp <- cbind(1:n.chamber.per.row[i] + i * 0.5,rep(i,n.chamber.per.row[i]))
xy <- rbind(xy,tmp)
}
return(xy)
}
my.B.mut <- function(B,k){
new.B <- B
n <- length(B[1,])
m <- length(B[,1])
rule1 <- FALSE
for(i in 1:m){
for(j in 1:n){
if(i == k || j == k){
rule1 <- TRUE
}else{
rule1 <- FALSE
}
if(rule1){
new.B[i,j] <- -B[i,j]
}else{
new.B[i,j] <- B[i,j] + 1/2 * (abs(B[i,k]) * B[k,j] + B[i,k] * abs(B[k,j]))
}
}
}
return(new.B)
}
n <- 4
out <- my.B.flagminor(n)
library(igraph)
g <- graph.adjacency(out$B)
lout <- my.layout.flagminor(n)
plot(g,layout = lout)
out$B.ext
my.B.mut(out$B.ext,2)
個の部分集合からなり、それらの包含関係は超立方体の形をしたポセットになっている
個できる
個の変異可能な頂点ができるので、拡大skew-symmetric 行列が作れる。
列で
行の行列
個のflag minorsの正の確認で済むことが導ける
