三角化のTeichmuller spaceのための基礎
- https://ryamada.hatenadiary.jp/entry/20200705/1593907656:こちらの記事で、genus 穴のある閉曲面特徴づけとしてTeichmuller spaceの基礎事項をまとめた
- 今回の記事は、閉曲面の三角メッシュの線の引き具合のTeichmuller spaceを考えるための基礎事項をまとめておく
- そもそも、閉曲面の三角メッシュがTeichmuller spaceの対象となる、とはどういうことか。。。
- 三角メッシュは、平面グラフであるから、「ある辺」を連続的に動かしても良いけれど、他の辺と交叉してはいけない、というルールの下で同一視することにすれば、閉曲面上にある数の点をおいた時に、そこに作れる三角メッシュのパターンは、位相的な情報になる
- 結局、三角化を位相的に捉えてTeichmuller spaceで扱う時に問題とする情報は:
- 閉曲面のgenus
- 閉曲面上の点の数
- 普通の三角メッシュと一般化した三角メッシュ
- いわゆる三角メッシュは、全ての三角形が、3点を結ぶ3辺があって、凸な形になっているものを言う
- 三角メッシュでは、2つの三角形の辺を貼り合わせてメッシュ化する
- いわゆる三角メッシュでは、辺の貼り合わせにあたり、異なる2つの三角形の辺の貼り合わせをする
- 一般化した三角メッシュでは、一つの三角形の2辺の貼り合わせも許可する
- これが違い
- 一般化三角メッシュによって、新たに登場するのは、「1つの三角形の隣り合う2辺を貼り合わせてできる形」である
- それは、1頂点から出て、その頂点に戻るループと、そのループの内部に1個の頂点とがあり、ループの始点・終点頂点とループ内部頂点とを結んだ形である。自己貼り合わせ三角形とでも呼ぶ形である
- ある頂点がループをもち、その内部に1頂点がある状態は、その2頂点に辺を引くと、自己張り合わせ三角形ができる。この自己貼り合わせ三角形を作りうる状態を once-punctured monogonと呼ぶ。monogonとは、1角形(頂点数が1で辺数が1の多角形)のことで、その内部にある頂点を「針刺し穴 puncture」と読んでいる
- Tagged arc
- once-punctured monogonを切り取るループは、三角化に当たって、特別な扱いをする必要が出てくる
- このonce-punctured monogonを切り取るループを、ループの始点・終点の頂点から、内部頂点への辺(arc)に対応づけて置き換えることにする
- こうすることで、一般化三角メッシュで、自己貼り合わせ三角形を含むメッシュであっても、「ループ」を持っていないとみなすことが可能になる
- しかしながら、このループを普通の辺に置き換えたことによって、この2頂点間には、二つの辺を考慮する必要が生じる
- 一つはもともとの普通の辺、もう一つは、once-punctured monogonを切り取るループを意味する「見かけ上の辺」
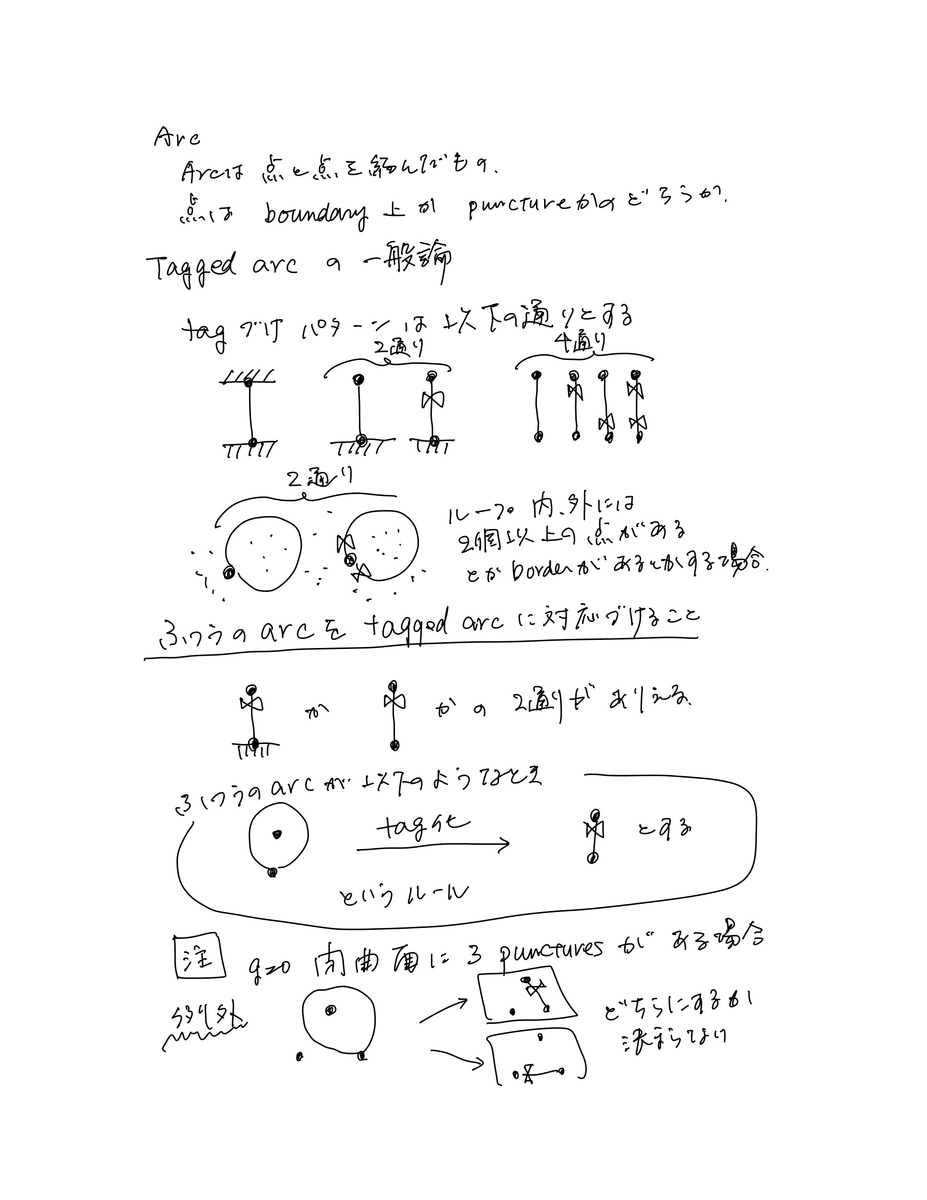
- 異なる2つは、区別できた方が良いので、ループに対応する方を、tagged arcとする。図示する時には、それとわかる印をつける
- なお、このonce-punctured monogonを切り取るループを表すtagged arcが大事だが、「そもそもtagged arcと言うものを導入するなら、それの一般化した定義をしておくのもよかろう」と言うことで、tagged arcとは、と言う定義が別途、存在することにも注意
- そのようなtagged arcの例として、2つのcusp型点を結ぶarcには両端のtag具合により4通りができる([1210.5569] Cluster algebras and triangulated surfaces. Part II: Lambda lengthsのFigure 7を参照)
- Tagged arc 導入の意義
- 三角化を考える時に、二つのグラフを用いる
- 一つは、取りうるあらゆる辺(arc)を頂点としたグラフでArc complexと呼ばれるもの。これは、ある一揃いのarc の部分集合があった時に、ある三角メッシュが出来上がるような時、そのarcの部分集合がクリークになっているようなグラフ
- もう一つは、arc complexの双対になるもので、Exchange complexと呼ばれるもの。これは、ある三角メッシュがあった時に、そのうちのただ1つのarcを別の特定のarcに入れ替えることで新たな三角メッシュができることを利用して、三角メッシュ同士の移り変わり関係を表したグラフ
- 今、arcを普通のarcにして、once-punctured monogonを切り取るarcを使ってarc complexを作り、その双対としてのexchange complexを作ると、ちょっと綺麗な関係にならないことが知られている
- once-punctured monogonを切り取るarcをtagged arcとして、それぞれのcomplexを作ると、対称性の高いグラフ(例えば、exchange complexなら、正則グラフ(全ての頂点の次数が等しいグラフ))になったりする
- また、この対称性が高いcomplexにできることが、団代数・団変数として取り扱う時に有用であることも、この記事を書いている目的と関係が深いので、あえて触れておく
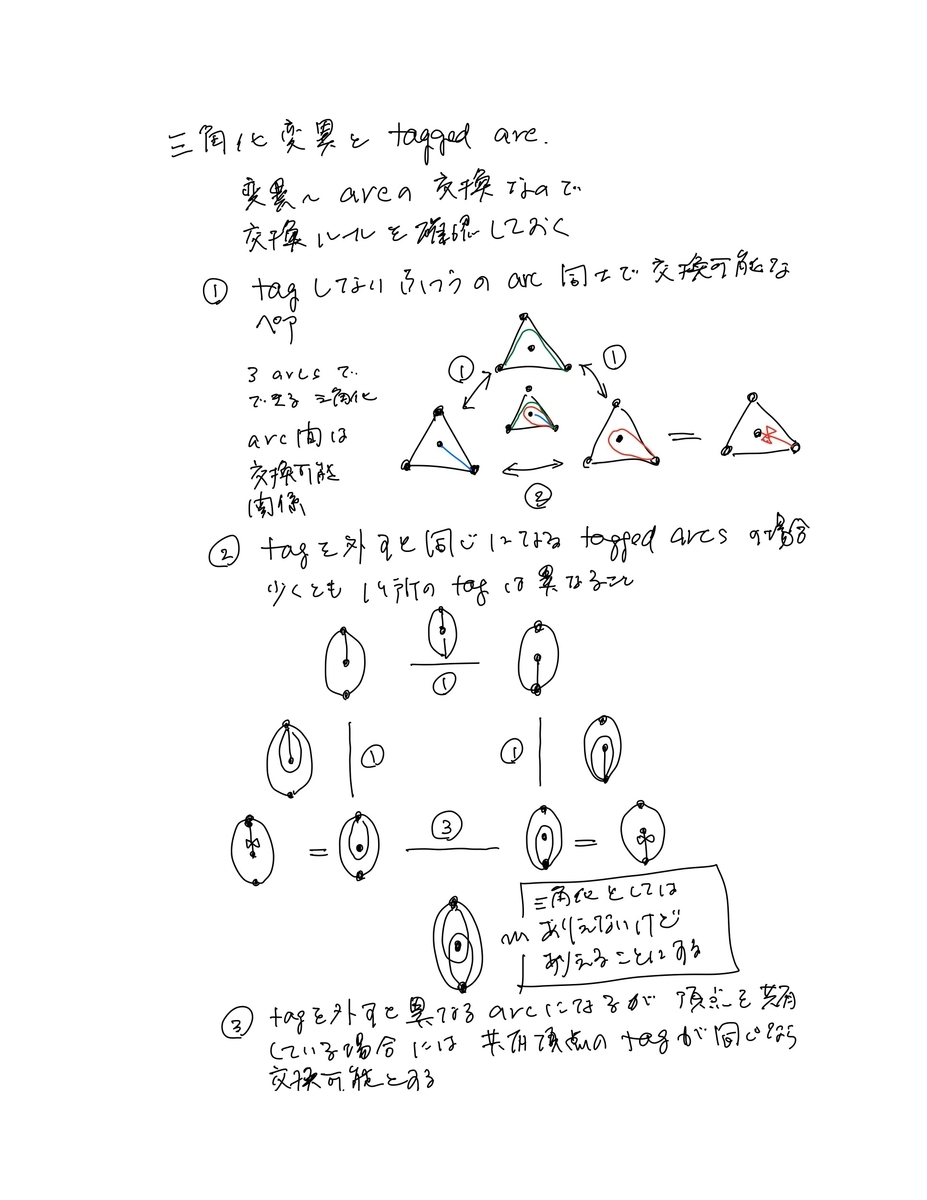
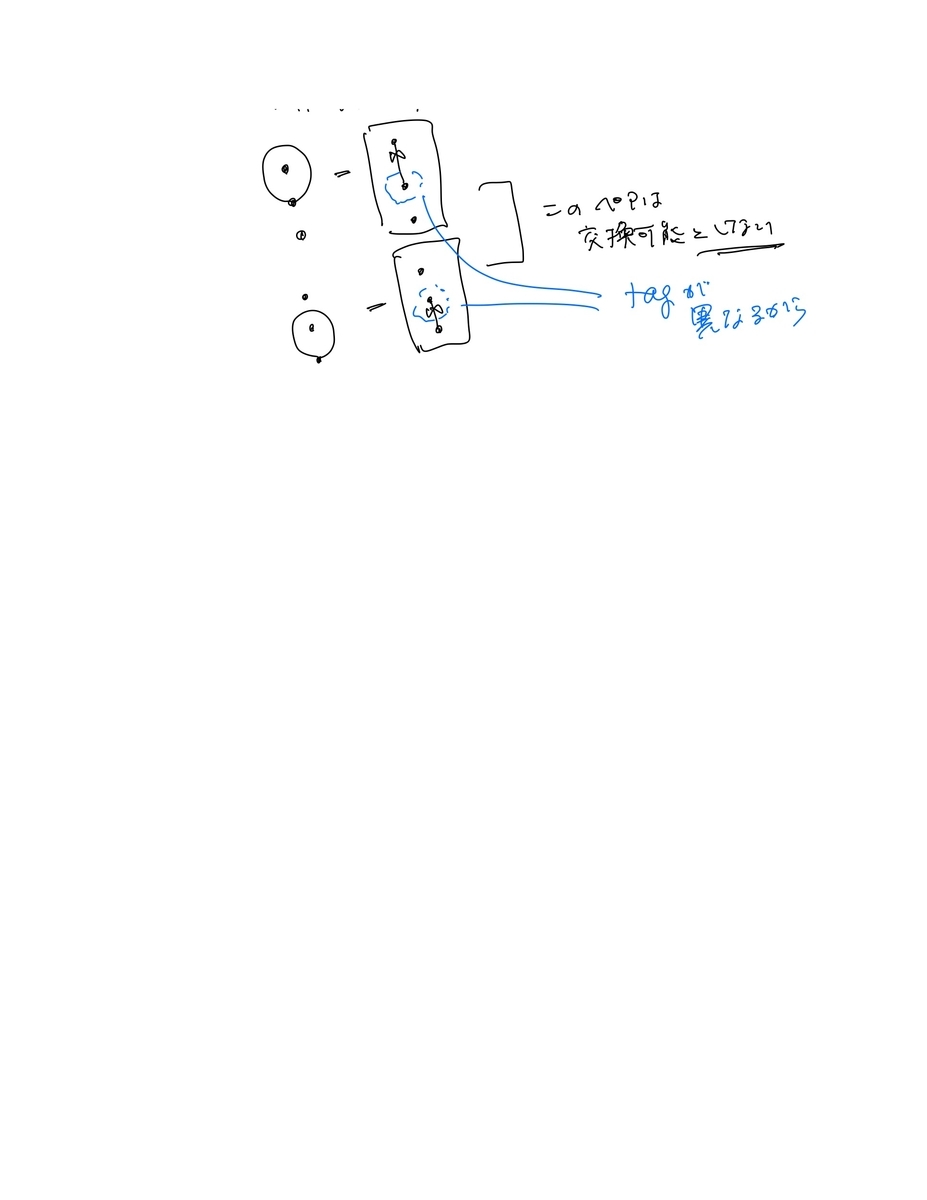
- tagged arcsの交換ルールを含め、tagged arcについて図を用いた説明を貼っておく
- 三角化と曲面トポロジー
- 三角化のパターンは、前項で書いたようにtagged arc、自己貼り合わせ三角形を許せば、団代数・団変数と繋がる「良い」形式にできる
- Teichmuller spaceが由来する曲面トポロジー的には、もう少し複雑になる
- Teichmuller spaceは定負曲率閉曲面に対して定まったから、閉曲面の三角化パターンも定負曲率閉曲面化したい
- そのために、閉曲面上の点(三角形)の頂点をそのまま、ただの閉曲面上の点として見ていたのでは、負曲率な曲面にならない
- 二つの方法がある
- 今、点を裾野をもつ山に飛ばす方法をcuspにする、と言い、小さな穴をぐるぐる巻きにする方法をboundaryにすると言う
- boundaryにした場合、arcのぐるぐる巻きには時計回りと反時計回りとの2通りがあり、それも区別するのが、定負曲率曲面のトポロジー分類風
- したがって、曲面上に点の数がN個あるときは、cuspにする個数kと、boundaryにする個数N-kとの場合分けがあり、boundaryにする方には
の場合分けが発生する
- つまり
の場合分けがある
- Teichmuller spaceでは、これらを全て区別する(こともある)
- この
は、多次元多面体構造をとり、その全ての単体要素が、個々の場合分けに対応する。例えば、N=3の場合には、正八面体になる。N=3なので3次元空間の多面体担っている。全てがboundaryの場合は、
通りあり、それが、8つの面に対応する。2つがboundaryで1つがcuspの場合は、boundaryの取り方が3通りで、それの巻き方の場合分けが4通りあることから、全部で12通りある。これは、正八面体の辺の数に相当する。boundaryが1個の場合は、3通りにつき、巻きの向きの2通りで、全部で6通り。これが正八面体の6頂点。最後に、全部がcuspの場合はただ一通りで、これを正八面体の重心〜原点に対応づける。例えば、ある面は3点がboundaryの場合である向きのぐるぐるだが、それにも色々な場合があることが、「面」の至る所が、曲面の様子に対応することからもわかる。そして、この3次元空間上の座標がTeichmuller spaceの座標となっており、それは、genusありの閉曲面に見つけた測地線的半ズボン切断閉曲線の長さから得られる座標になっている。参考:
Shift coordinates, stretch lines and polyhedral structures for Teichmüller space | SpringerLinkのFigure 11
-
- 他方、三角化のみに興味があるときは、この場合分けは、結局のところ同じ三角化なので、同一視したくなることもある
- Arc同士の相互関係と団変数
- Arcには団変数が付随する
- 団変数は、ある三角化をシードとした時に、その辺の数の団変数セットを用いて、シードに含まれない全ての団変数が有理式で表される。実際には、分母が単項であるローラン多項式になる
- あるarcをあるシード団変数セットのローラン多項式で表した時、その分母の単項に現れる、あるシード変数の次数は、曲面上で、2つのarcを素直に引いた時の交叉数になると言う性質がある
- ある三角化では全ての辺が交叉しないので、分母は1である(全ての辺の団変数は、相互に独立)
- 三角化の変異をしていくと、だんだん、分母の次数が上がってくるが、それは、三角化の違いの程度をある意味で表していると言える
- ちなみに、tagged arcで考える時、この「交叉数」は少しルールを入れる必要があることに注意。ただし、意味合いとしては、arc同士の関係が団変数の分母の次数によって表現されると言うことは、団代数・団変数と三角化の幾何とを結ぶ情報となる