遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

移動と格子と結晶

格子 移動 結晶 準結晶
  • 昨日、移動のことをメモした
  • 結晶というのは、"Mathematical model for ideal crystal (or perfect crystal) in R^d is a set Λ, which is formed by a finite number of shifted copies of a single lattice L. Formally, Λ is a perfect crystal if Λ = L + S, where S is a finite set of translations. Since lattices satisfy L − L ⊂ L and a perfect crystal satisfies Λ − Λ ⊂ Λ − S, they are both Meyer sets. The Meyer concept of quasicrystals thus generalizes the classical definition of crystals. Perfect crystal is however a periodic set, i.e. Λ + x ⊂ Λ for any x ∈ L, and therefore it is not a suitable model for quasicrystalline materials, which reveal rotational symmetries ncompatible with periodicity. We shall now describe a large class of Meyer sets which are not invariant under translation."とこちらにあるように、「シフト」したときに重ね合わせられる
  • このことと「移動」とその距離の評価という点から考えると、「シフトして重ねあわせた」とき、その移動量は、すべての点が同じだけ動いたものとして、その量を点の数で倍するとみなしてもよいし。重なった点は不動で、端の点だけが長距離移動したと考えてもよい
  • どちらの計算方法でも、移動距離の総量は変わらない、という評価法である
  • 点集合の移動量の総量も同様に考えることができる
  • では、各点の移動量の総量よりも移動のベクトルの具合について興味があるときはどうなるだろうか
  • 総量だけで比べれば同じだけれど、平行移動と端点のみの長距離移動は区別したい
  • そのようにするには、すべての点の移動の総和や総平均に着目するのではなくて、その分散・ばらつきに注意するのがよい
  • そんなことを考えて作ったのが昨日の記事の、「内積」利用の評価指標


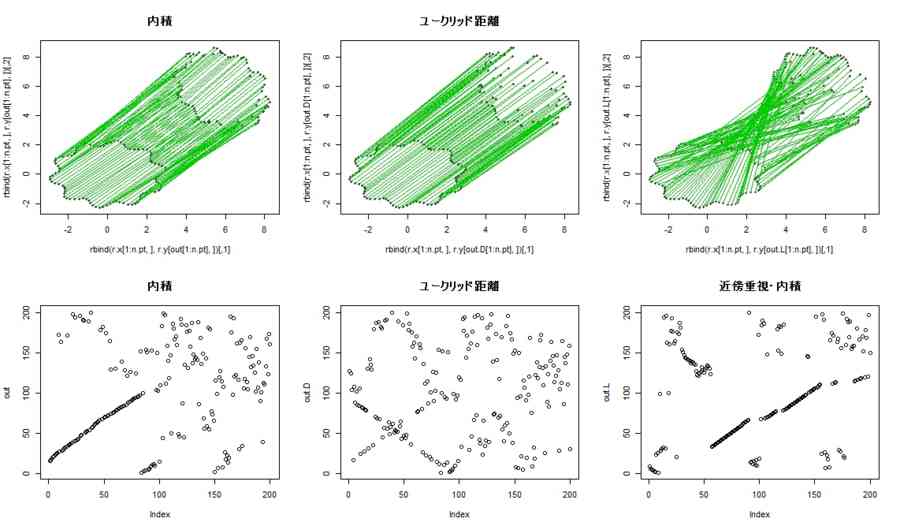
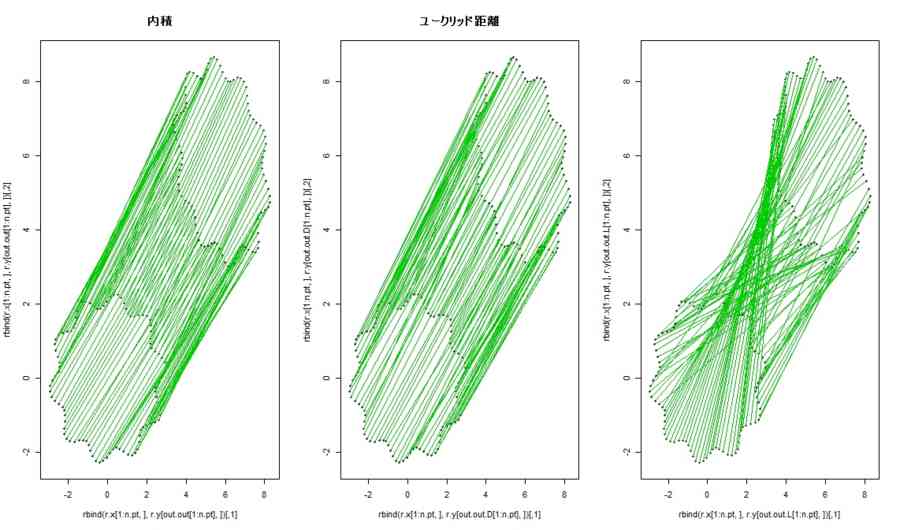
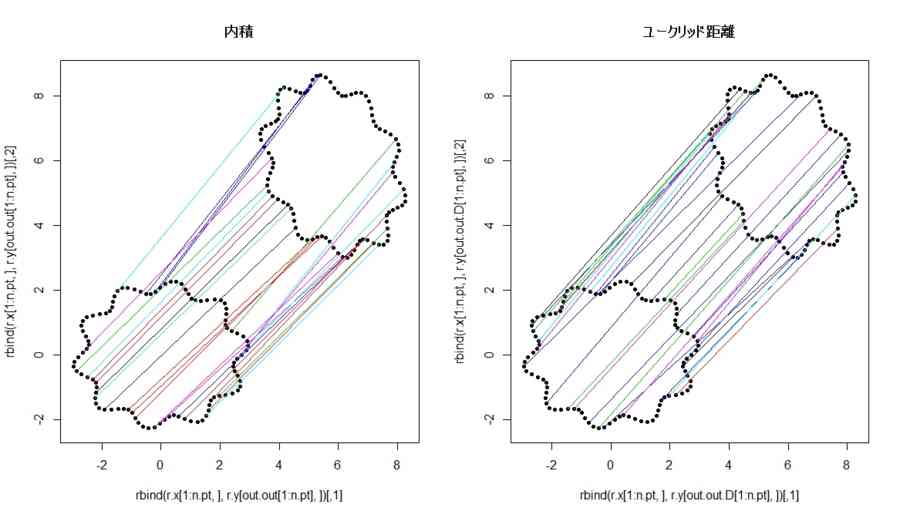
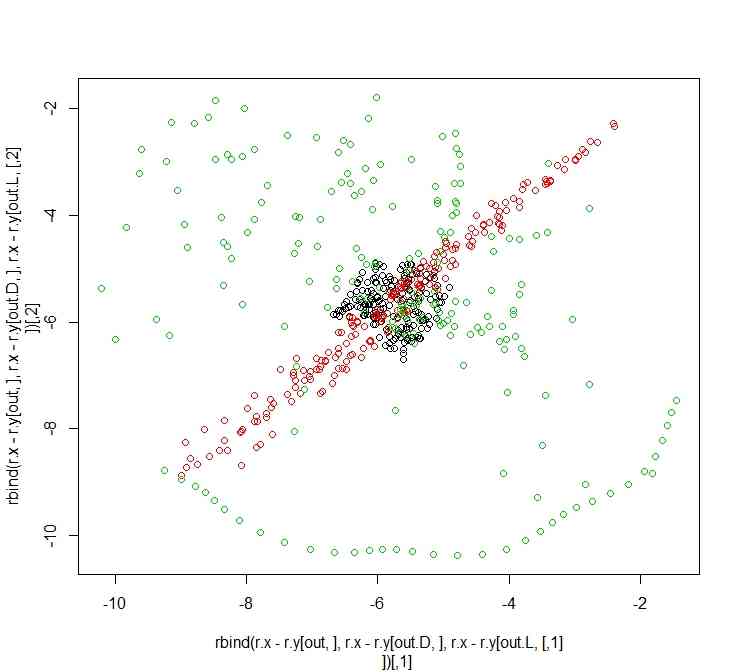
  • すべてのベクトルが似たような方向・長さになっているかどうかを強調したのが次の図であり、そのベクトルを散布図表示もしてみた


library(geometry)
d <- 2
n.pt <- 100
#X <- matrix(rnorm(n.pt*d),ncol=d)
#Y <- X + 1 + rnorm(length(X),0,0.1)
t <- seq(from=0,to=1,length=n.pt)*2*pi
R.X <- 0.2*sin(t*10)+2.1
X <- cbind(R.X*cos(t)*1.3,R.X*sin(t))
Y <- cbind(X[,1],X[,2])
theta <- pi/3
Rot <- matrix(c(cos(theta),sin(theta),-sin(theta),cos(theta)),2,2)
Y <- Y %*% Rot
#X <- X + rnorm(length(X),0,0.1)
#Y <- Y + rnorm(length(Y),3,0.1)
Y <- (Y-min(Y)) + 3
#Y[,1] <- (Y[,1]-min(Y[,1]))^1.3
# そのままの三角形分割
delaunay.X <- delaunayn(X)
plot(X)
delaunay.X.2 <- rbind(delaunay.X[,1:2],delaunay.X[,2:3],delaunay.X[,c(3,1)])
segments(X[delaunay.X.2[,1],1],X[delaunay.X.2[,1],2],X[delaunay.X.2[,2],1],X[delaunay.X.2[,2],2])
segments(X[delaunay.X.2[,1],1],X[delaunay.X.2[,1],2],X[delaunay.X.2[,2],1],X[delaunay.X.2[,2],2])

# 凸包化
X.hull <- t(convhulln(X))
Y.hull <- t(convhulln(Y))

plot(X,pch=20)
segments(X[X.hull[1,],1],X[X.hull[1,],2],X[X.hull[2,],1],X[X.hull[2,],2])
plot(Y,pch=20)
segments(Y[Y.hull[1,],1],Y[Y.hull[1,],2],Y[Y.hull[2,],1],Y[Y.hull[2,],2])

X.h <- X[unique(c(X.hull)),]
Y.h <- Y[unique(c(Y.hull)),]
plot(X.h)

# 凸包の三角形分割

delaunay.X.h <- delaunayn(X.h)
plot(X.h)
delaunay.X.h.2 <- rbind(delaunay.X.h[,1:2],delaunay.X.h[,2:3],delaunay.X.h[,c(3,1)])
segments(X.h[delaunay.X.h.2[,1],1],X.h[delaunay.X.h.2[,1],2],X.h[delaunay.X.h.2[,2],1],X.h[delaunay.X.h.2[,2],2])
plot(Y.h)
delaunay.Y.h <- delaunayn(Y.h)
plot(Y.h)
delaunay.Y.h.2 <- rbind(delaunay.Y.h[,1:2],delaunay.Y.h[,2:3],delaunay.Y.h[,c(3,1)])
segments(Y.h[delaunay.Y.h.2[,1],1],Y.h[delaunay.Y.h.2[,1],2],Y.h[delaunay.Y.h.2[,2],1],Y.h[delaunay.Y.h.2[,2],2])

# ドロネー三角形の体積計算
# Determinantを使って体積を計算する
my.simplex.volume <- function(V,factorial=FALSE){
	n <- length(V[1,])
	K <- matrix(V[1:n,],ncol=n)
	K. <- t(K)-V[n+1,]
	if(factorial){
		return(det(K.)/factorial(n))
	}else{
		return(det(K.))
	}
	
}
# 頂点座標の行列Xと頂点IDベクトルaとから単体体積を計算する関数
my.delaunay.vol <- function(a,X){
	tmp <- matrix(X[a,],ncol=length(X[1,]))
	my.simplex.volume(tmp)
}
# すべての凸包の三角形分割のドロネー単体体積を計算
spx.vol.x <- apply(delaunay.X.h,1,my.delaunay.vol,X.h)
spx.vol.y <- apply(delaunay.Y.h,1,my.delaunay.vol,Y.h)

spx.vol.x.st <- abs(spx.vol.x)/sum(abs(spx.vol.x))
spx.vol.y.st <- abs(spx.vol.y)/sum(abs(spx.vol.y))

n.r.pt <- 100
r.x <- r.y <- matrix(0,n.r.pt,d)
spx.vol.x.st.cum <- cumsum(spx.vol.x.st)
x.rd <- round(spx.vol.x.st.cum*n.r.pt)
r.n.x <- c(x.rd[1],diff(x.rd))
r.n.x

spx.vol.y.st.cum <- cumsum(spx.vol.y.st)
y.rd <- round(spx.vol.y.st.cum*n.r.pt)
r.n.y <- c(y.rd[1],diff(y.rd))
r.n.y

tri.id.x <- sample(1:length(spx.vol.x.st),n.r.pt,replace=TRUE,prob=spx.vol.x.st)
tri.id.y <- sample(1:length(spx.vol.y.st),n.r.pt,replace=TRUE,prob=spx.vol.y.st)
library(MCMCpack)
cnt <- 1
for(i in 1:length(spx.vol.x.st)){
	tmp.id <- cnt:(cnt+r.n.x[i]-1)
	cnt <- cnt+r.n.x[i]
	tmp.n <- r.n.x[i]
	if(tmp.n>0){
		tmp.r <- rdirichlet(tmp.n,rep(1,length(delaunay.X.h[i,])))
		tmp.X <- tmp.r %*% X.h[delaunay.X.h[i,],] 
		r.x[tmp.id,] <- tmp.X
	}
}
cnt <- 1
for(i in 1:length(spx.vol.y.st)){
	tmp.id <- cnt:(cnt+r.n.y[i]-1)
	cnt <- cnt+r.n.y[i]
	tmp.n <- r.n.y[i]
	if(tmp.n>0){
		tmp.r <- rdirichlet(tmp.n,rep(1,length(delaunay.Y.h[i,])))
		tmp.Y <- tmp.r %*% Y.h[delaunay.Y.h[i,],] 
		r.y[tmp.id,] <- tmp.Y
	}
}

plot(X.h)
delaunay.X.h.2 <- rbind(delaunay.X.h[,1:2],delaunay.X.h[,2:3],delaunay.X.h[,c(3,1)])
segments(X.h[delaunay.X.h.2[,1],1],X.h[delaunay.X.h.2[,1],2],X.h[delaunay.X.h.2[,2],1],X.h[delaunay.X.h.2[,2],2])
points(r.x,pch=20,col=2)
plot(Y.h)
delaunay.Y.h.2 <- rbind(delaunay.Y.h[,1:2],delaunay.Y.h[,2:3],delaunay.Y.h[,c(3,1)])
segments(Y.h[delaunay.Y.h.2[,1],1],Y.h[delaunay.Y.h.2[,1],2],Y.h[delaunay.Y.h.2[,2],1],Y.h[delaunay.Y.h.2[,2],2])
points(r.y,pch=20,col=2)

r.x <- rbind(X,r.x)
r.y <- rbind(Y,r.y)
out <- my.move(r.x,r.y)
out.D <- my.move.D(r.x,r.y)
out.L <- my.move.L(r.x,r.y)
par(mfcol=c(2,3))
plot(rbind(r.x[1:n.pt,],r.y[out[1:n.pt],]),pch=20,col=rep(1:2,each=length(r.x[,1])),main="内積")
for(i in 1:n.pt){
	segments(r.x[i,1],r.x[i,2],r.y[out[i],1],r.y[out[i],2],col=3)
}
plot(out,main="内積")
plot(rbind(r.x[1:n.pt,],r.y[out.D[1:n.pt],]),pch=20,col=rep(1:2,each=length(r.x[,1])),main="ユークリッド距離")
for(i in 1:n.pt){
	segments(r.x[i,1],r.x[i,2],r.y[out.D[i],1],r.y[out.D[i],2],col=3)
}
plot(out.D,main="ユークリッド距離")
plot(rbind(r.x[1:n.pt,],r.y[out.L[1:n.pt],]),pch=20,col=rep(1:2,each=length(r.x[,1])))
for(i in 1:n.pt){
	segments(r.x[i,1],r.x[i,2],r.y[out.L[i],1],r.y[out.L[i],2],col=3,main="近傍重視・内積")
}
plot(out.L,main="近傍重視・内積")
par(mfcol=c(1,1))
plot(rbind(r.x-r.y[out,],r.x-r.y[out.D,],r.x-r.y[out.L,]),col=rep(1:3,each=length(r.x[,1])))
plot(rbind((r.x-r.y[out,])[1:n.pt,],(r.x-r.y[out.D,])[1:n.pt,],(r.x-r.y[out.L,])[1:n.pt,]),col=rep(1:3,each=n.pt))

out.out <- my.move.D(r.y[out[1:n.pt],],r.y[1:n.pt,])
out.out.D <- my.move.D(r.y[out.D[1:n.pt],],r.y[1:n.pt,])
out.out.L <- my.move.D(r.y[out.L[1:n.pt],],r.y[1:n.pt,])

par(mfcol=c(1,3))
plot(rbind(r.x[1:n.pt,],r.y[out.out[1:n.pt],]),pch=20,col=rep(1:2,each=length(r.x[,1])),main="内積")
for(i in 1:n.pt){
	segments(r.x[i,1],r.x[i,2],r.y[out.out[i],1],r.y[out.out[i],2],col=3)
}
plot(rbind(r.x[1:n.pt,],r.y[out.out.D[1:n.pt],]),pch=20,col=rep(1:2,each=length(r.x[,1])),main="ユークリッド距離")
for(i in 1:n.pt){
	segments(r.x[i,1],r.x[i,2],r.y[out.out.D[i],1],r.y[out.out.D[i],2],col=3)
}
plot(rbind(r.x[1:n.pt,],r.y[out.out.L[1:n.pt],]),pch=20,col=rep(1:2,each=length(r.x[,1])))
for(i in 1:n.pt){
	segments(r.x[i,1],r.x[i,2],r.y[out.out.L[i],1],r.y[out.out.L[i],2],col=3,main="近傍重視・内積")
}
par(mfcol=c(1,1))
par(mfcol=c(1,2))
plot(rbind(r.x[1:n.pt,],r.y[out.out[1:n.pt],]),pch=20,col=rep(1:2,each=length(r.x[,1])),main="内積")
for(i in 1:n.pt){
	if(runif(1) < 0.3){
		segments(r.x[i,1],r.x[i,2],r.y[out.out[i],1],r.y[out.out[i],2],col=sample(1:6,1))
	}

}
plot(rbind(r.x[1:n.pt,],r.y[out.out.D[1:n.pt],]),pch=20,col=rep(1:2,each=length(r.x[,1])),main="ユークリッド距離")
for(i in 1:n.pt){
	if(runif(1)<0.3){
		segments(r.x[i,1],r.x[i,2],r.y[out.out.D[i],1],r.y[out.out.D[i],2],col=sample(1:6,1))
	}
	
}
par(mfcol=c(1,1))

# ノード対応づけをするために試行錯誤した関数
# マッチングでできたペアの距離にした
my.move <- function(x,y,w.x=NULL,w.y=NULL){
	if(!is.matrix(x)){
		x <- matrix(x,ncol=1)
	}
	if(!is.matrix(y)){
		y < matrix(y,ncol=1)
	}
	if(is.null(w.x)){
		w.x <- rep(1,length(x[,1]))
	}
	if(is.null(w.y)){
		w.y <- rep(1,length(y[,1]))
	}
	D <- x %*% t(y)
	D <- D-min(D)
	xy <- rbind(x,y)
	m.xy <- apply(xy,2,mean)
	x.d <- t(t(x)-m.xy)
	y.d <- t(t(y)-m.xy)
	W <- outer(w.x,w.y,"*")
	D <- D * W
	
	as.vector(solve_LSAP(D,maximum=TRUE))
}
my.move.D <- function(x,y,w.x=NULL,w.y=NULL){
	if(!is.matrix(x)){
		x <- matrix(x,ncol=1)
	}
	if(!is.matrix(y)){
		y < matrix(y,ncol=1)
	}
	if(is.null(w.x)){
		w.x <- rep(1,length(x[,1]))
	}
	if(is.null(w.y)){
		w.y <- rep(1,length(y[,1]))
	}
	D <- (as.matrix(dist(rbind(x,y))))[1:length(x[,1]),(1+length(x[,1])):(2*length(x[,1]))]
	#D <- D-min(D)
	xy <- rbind(x,y)
	m.xy <- apply(xy,2,mean)
	W <- outer(w.x,w.y,"*")
	D <- D * W
	
	as.vector(solve_LSAP(D,maximum=FALSE))
}
my.move.L <- function(x,y,w.x=NULL,w.y=NULL){
	if(!is.matrix(x)){
		x <- matrix(x,ncol=1)
	}
	if(!is.matrix(y)){
		y < matrix(y,ncol=1)
	}
	if(is.null(w.x)){
		w.x <- rep(1,length(x[,1]))
	}
	if(is.null(w.y)){
		w.y <- rep(1,length(y[,1]))
	}
	D <- x %*% t(y)
	D <- D-min(D)
	xy <- rbind(x,y)
	m.xy <- apply(xy,2,mean)
	x.d <- t(t(x)-m.xy)
	y.d <- t(t(y)-m.xy)
	L.x <- sqrt(apply(x.d^2,1,sum))
	L.y <- sqrt(apply(y.d^2,1,sum))
	LL <- outer(L.x,L.x,"*")
	L.q <- quantile(LL,0.05)
	LL.q <- sign(LL < L.q)
	W <- outer(w.x,w.y,"*")
	D <- D * W * LL.q
	
	as.vector(solve_LSAP(D,maximum=TRUE))
}