尾根

• 山の頂は、全微分が０の点(谷底も)
• 尾根っていうのは(谷筋も)っていうのは、全微分は０ではないが、ある方向に勾配があって、それに垂直な方向の２階の微分が０であるようなところ(言い換えると、１階の微分ベクトル方向と２階の微分ベクトル方向が一致(逆向きを含めて)のところ)らしい
• Rでやってみる(殴り書き…)
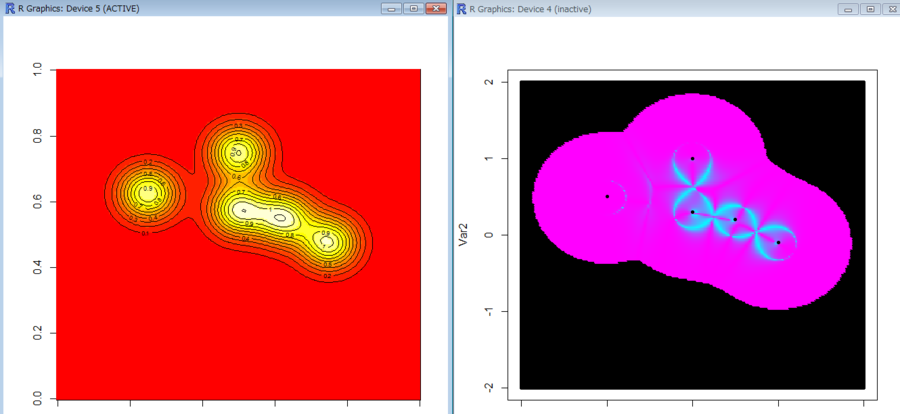
• ピンクの筋が尾根筋・谷筋。水色のところは１階微分のベクトルと２階の微分のベクトルとが垂直なところ

t <- seq(from=0,to=1,length=1000)*10
x <- exp(0.1*t)*cos(t)
y <- exp(0.05*t)*sin(t)
#x <- t
#y <- t^2
X <- cbind(x,y)
X. <- X + rnorm(length(X))*0.05

plot(X.,pch=20)
lines(X,type="l",col=2)

n.pt <- 20
s <- 0.01
for(i in 1:length(t)){
	R <- matrix(rnorm(n.pt*length(X[1,]),0,s),nrow=n.pt)
	points(t(t(R)+X.[i,]),pch=20,cex=0.1,col=3)
}

my.grad <- function(x,X,s=1){
	tmp <- t(-t(X) + x)
	# 観測点を原点とした、x方向の単位ベクトルと距離
	Rsq.tmp <- apply(tmp^2,1,sum)
	R.tmp <- sqrt(Rsq.tmp)
	tmp.st <- tmp/R.tmp
	d0 <- sum(exp(-Rsq.tmp/(2*s)))
	# １次微分の重み
	w <- (-R.tmp/s) * exp(-Rsq.tmp/(2*s))
	d1 <- apply(tmp.st * w,2,sum)
	tmp.st2 <- -tmp.st
	w2 <- (Rsq.tmp/(s^2)-1/s) * exp(-Rsq.tmp/(2*s))
	d2 <- apply(tmp.st2 * w2,2,sum)
	return(list(d0=d0,d1=d1,d2=d2))
}

X. <- matrix(c(-1,1,0.5,0,0,0.5,-0.1,0.2,0.3,1),ncol=2)
t <- seq(from=-2,to=2,length=200)
y <- as.matrix(expand.grid(t,t))
n.y <- length(y[,1])
tmp.outs <- matrix(0,n.y,length(X.[1,]))
tmp.outs2 <- matrix(0,n.y,length(X.[1,]))
dens <- rep(0,n.y)
tmp.theta <- rep(0,length(n.y))
plot(rbind(X.,y),pch=20,cex=0.001,col=c(rep(1,length(X.[,1])),rep(2,n.y)))
#plot(rbind(X.),pch=20,cex=0.001,col=c(rep(1,length(X.[,1])),rep(2,n.y)))
points(X.,pch=20,cex=1,col=1)

s <- 0.05


for(i in 1:n.y){
	g <- my.grad(y[i,],X.,s=s)
	dens[i] <- g$d0
	tmp.outs[i,] <- g$d1
	tmp.outs2[i,] <- g$d2
	ip <- sum(tmp.outs[i,] * tmp.outs2[i,])/sqrt(sum(tmp.outs[i,]^2)*sum(tmp.outs2[i,]^2))
	if(abs(ip)>1) ip <- sign(ip)*1
	#tmp.theta[i] <- (asin(ip)+pi/2)/pi
	tmp.theta[i] <- abs(asin(ip))/pi*2
	col <- rgb(tmp.theta[i],1-tmp.theta[i],1)
	if(sqrt(sum(tmp.outs[i,]^2))<0.01) col <- rgb(0,0,0)
	tmp.outs[i,] <- tmp.outs[i,]/sqrt(sum(tmp.outs[i,]^2))*tmp.theta[i]
	tmp.outs2[i,] <- tmp.outs2[i,]/sqrt(sum(tmp.outs2[i,]^2))*tmp.theta[i]
	
	points(y[i,1],y[i,2],pch=20,col=col)
	#segments(y[i,1],y[i,2],y[i,1]-tmp.outs[i,1],y[i,2]-tmp.outs[i,2],col=2)
	#segments(y[i,1],y[i,2],y[i,1]-tmp.outs2[i,1],y[i,2]-tmp.outs2[i,2],col=3)
}
points(X.,pch=20)
dev.new()
image(matrix(dens,ncol=length(t)))
contour(matrix(dens,ncol=length(t)),add=TRUE)