Runge-Kuttaで微分方程式の数値計算

• 式に解けない微分方程式は、微分方程式によって微小時間あたりの変化量を計算し、それの積み重ねとして、初期値から一定時間後の変数の値を計算する
• ただし、単純に微分の値と微小時間の積でやると、ずれが蓄積して来るので工夫が必要
• その一つの方法がRunge-Kutta
• RのdeSoloveパッケージRunge-Kutta法とその関連法を扱うrk()や、それ以外の方法があり、微分方程式と初期値が与えられた時に、数値計算してくれる
• 以下はRunge-Kutta法関係のそれ

library(deSolve)
# 微分方程式
# この関数my.ODEに 引数 t は使われていないが
# runge-kuttaの本体関数 rk() との関係で、この引数は必要(らしい)
# 時刻を表す引数
# xは対象となっている変数の値のベクトル
# parmsは微分方程式の係数
# 差分を計算して返す
# この連立微分方程式はロトカ=ヴォルテラ
# parms[1],parms[4]は負、parms[2],parms[3]は正
my.ODE <- function(t, x, parms)  {

	dX <- (parms[1] + parms[2]*x[2])*x[1]
	dY <- (parms[3] + parms[4]*x[1])*x[2]

	res <- c(dX, dY)
	list(res)

}

## The parameters 
# 連立微分方程式の４係数を決める
library(MCMCpack)
A <- rdirichlet(1,rep(1,4))*5
A[c(1,4)] <- -A[c(1,4)]

## vector of timesteps
# 計算する時刻
times <- seq(0, 100, length = 1001)

## 初期値
# 固定点の周囲から始まるとうまく周期性を出すので
# 固定点に若干のずれを入れる
xstart <- c(-A[3]/A[4], -A[1]/A[2]) + rnorm(2)*0.1

## Euler method
# hini 計算するための時間差分
out1  <- rk(xstart, times, my.ODE, A, hini = 0.1, method = "euler")

## classical Runge-Kutta 4th order
# hini 計算するための時間差分
out2 <- rk(xstart, times, my.ODE, A, hini = 1, method = "rk4")

## Dormand-Prince method of order 5(4)
# hmax この方法は時間差分が可変(ずれが大きくなりすぎないように可変)なので、その時間差分の最大値を指定
out3 <- rk(xstart, times, my.ODE, A, hmax = 1, method = "rk45dp7")

par(mfcol=c(1,3))
xlim <- range(out3[,2]) + c(-0.2,0.2)
ylim <- range(out3[,3]) + c(-0.2,0.2)
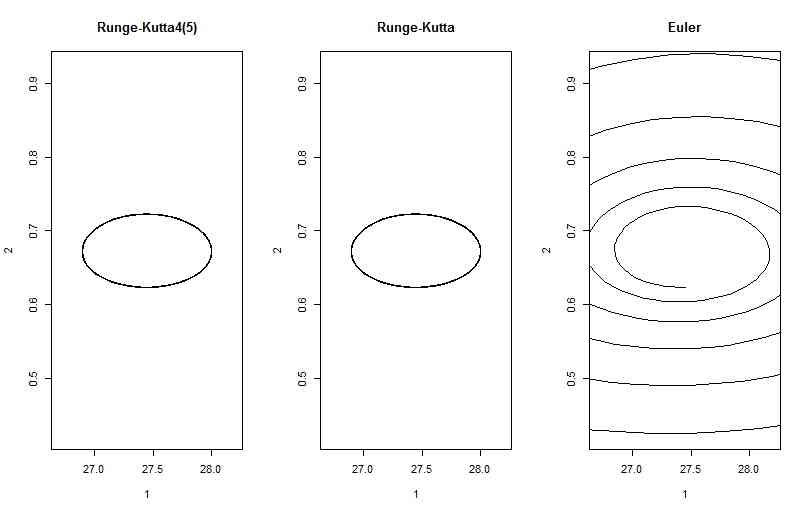
plot(out3[,2:3],type="l",xlim=xlim,ylim=ylim,main="Runge-Kutta4(5)")
plot(out2[,2:3],type="l",xlim=xlim,ylim=ylim,main="Runge-Kutta")
plot(out1[,2:3],type="l",xlim=xlim,ylim=ylim,main="Euler")
par(mfcol=c(1,1))