2012-06-15

ぱらぱらめくる『Simulation and Inference for Stochastic Differential Equations: With R Examples』1. 確率過程とそれを理解するための基礎。Ito過程。確率微分方程式とは

1. Stochastic Processes and Stochastic Differential Equations
- 確率空間と確率過程の数学的記法
- 確率変数の平均・分散・モーメント
- シミュレーションのための道具
  - 疑似乱数列
  - モンテカルロ法
  - 分散を小さくするための手法
    - モンテカルロはよい方法だが、あまりにナイーブにやりすぎると、収束が遅くて使えない(使いにくい)。その理由は、分散(信頼区間)が広すぎることに起因する(ことが多い)。それを解決するために、「早く収束させる」技術がいくつかある
- 確率過程は「経路・道」
- 確率過程のばらつき
  - Simple variationとquadratic variation (１次と２次)
- 確率過程の特徴づけ
  - モーメント、共分散、増分
- ブラウン運動
  - ３つのシミュレーション方法
    - 増分を正規分布でとる
    - 酔歩(-1,1)の繰り返し
    - Karhunen-Loeve 拡張(たくさんのものの足し合わせの極限としての定義がある。その足し合わせをある程度すれば、シミュレーションとしては精度が出る、といった感じの「定義とシミュレーション法」)
  - どれがよい？
    - ある時点の状態分布を取るだけなら、増分を正規分布でとるだけで十分
    - 経過を問題にするならKarhunen-Loeve 拡張がよい
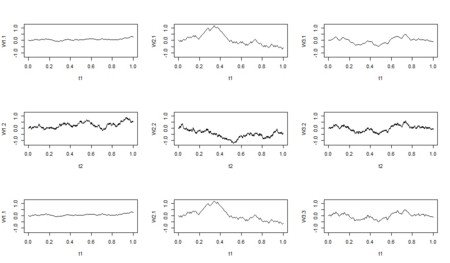
  - ３列はそれぞれ、左から「増分＝正規分布」「酔歩」「Karhunen-Loeve拡張」
  - ３行はそれぞれ、上から、時刻数が100,1000,100、Karhunen-Loeve拡張での重ね合わせ数50,50,10000
  - 時刻数を増やすと経過時間が伸びるのが「増分・正規」「酔歩」。「Karhunen-Loeve拡張」は増えていない
  - 「Karhunen-Loeve拡張」は時刻数を増やしても、重ね合わせ数を増やしても「細かさが増える」

N1<-100
N2<-1000
T<-1
Delta1<-T/N1
Delta2<-T/N2
W1.1<-W2.1<-W3.1<-numeric(N1+1)
W1.2<-W2.2<-W3.2<-numeric(N2+1)
W3.3<-numeric(N1+1)
t1<-seq(from=0,to=T,length=N1+1)
t2<-seq(from=0,to=T,length=N2+1)
# 単位時間当たりの増分を正規分布から乱数発生する
set.seed(123)
W1.1<-c(0,cumsum(rnorm(N1)*sqrt(Delta)))
set.seed(123)
W1.2<-c(0,cumsum(rnorm(N2)*sqrt(Delta)))

# 酔歩
set.seed(123)
W2.1<-c(0,cumsum(sample(c(-1,1),N1,replace=TRUE)))/sqrt(N1)
set.seed(123)
W2.2<-c(0,cumsum(sample(c(-1,1),N2,replace=TRUE)))/sqrt(N2)

# Karhunen-Loeve expansion
# 足し合わせる分布数を指定するパラメタが増える
n1<-50
n2<-10000
set.seed(123)
Z1<-rnorm(n1)
phi<-function(i,t,T){
	(2*sqrt(2*T))/((2*i+1)*pi) * sin(((2*i+1)*pi*t)/(2*T))
}
for(i in 1:n1){
	W3.1<-W3.1+Z1[i]*phi(i,t1,T)
}
set.seed(123)
Z2<-rnorm(n2)
for(i in 1:n2){
	W3.2<-W3.2+Z2[i]*phi(i,t2,T)
}
for(i in 1:n2){
	W3.3<-W3.3+Z2[i]*phi(i,t1,T)
}

ylim<-range(W1.1,W2.1,W3.1,W1.2,W2.2,W3.2,W3.3)
par(mfcol=c(3,3))
plot(t1,W1.1,type="l",ylim=ylim)
plot(t2,W1.2,type="l",ylim=ylim)
plot(t1,W1.1,type="l",ylim=ylim)
plot(t1,W2.1,type="l",ylim=ylim)
plot(t2,W2.2,type="l",ylim=ylim)
plot(t1,W2.1,type="l",ylim=ylim)
plot(t1,W3.1,type="l",ylim=ylim)
plot(t2,W3.2,type="l",ylim=ylim)
plot(t1,W3.3,type="l",ylim=ylim)
par(mfcol=c(1,1))

- いたるところ微分不可能
- ブラウン運動の拡張例
  - ブラウン運動の軌跡を作り、それを関数に与えて作る(たとえば指数関数的増加のブラウン運動)
  - 特定の２時刻の状態を通るようにする(ブラウン運動を作った後で、「通るように」変換)
- 確率的積分と確率的微分方程式
  - いたるところ微分不可能
  - 微分の式はできるが(確率的微分方程式)、そこに、無限小時間で発散する項が入っているので、意味がない…。意味がないけれど、微分方程式の係数は求めたい…
    - 確率微分方程式の例： $dS(t)=\mu S(t) dt + \sigma S(t) dW(t)$ の $dW(t)$ がWiener過程になっていて、これは、「いたるところ微分不可能」なので、この式自体をそのまま扱うことはしない
  - 積分はできる過程はある(Ito sum, Ito integralが可能な過程: Ito 過程)
    - 部分ごとに近似した積分を取る
    - 部分をどんどん狭くして、極限を取る
- Ito 過程の特徴
  - Ito 積分の期待値は0
  - Ito 積分の分散は確率変数の２乗の期待値の積分に同じ
  - Ito 過程のIto 積分は線形性がある
  - 時間の関数で定まるその他の特徴
  - マルチンゲール性(Wiki)のこと
- 拡散過程
  - ドリフト(どこかへ向かっていく項)と拡散の２項からなる
    - $dS(t)=\mu S(t) dt + \sigma S(t) dW(t)$
  - いくつかの過程(取扱いを可能にするための)
  - 不等式で示されるいくつかの特徴
- エルゴード的(Wiki)
- マルコフ性(Wiki)
- 拡散過程のinfinitesimal generator
- Ito 公式
  - 確率過程の計算に重要
  - シミュレーションにも重要
  - テイラー展開の確率過程版
- Ito 公式はよいが、実用(シミュレーションにも、微分方程式の解法にも(?))には工夫が必要
  - 変換する
  - 測度を変える
  - 尤度を計算しやすくする
- Parametric families of stochastic processes(使いやすいいくつかの確率過程)
  - The Ornstein-Uhlenbech or Vasicek process
  - The Black-Scholes-Merton or geometric Brownian motion model
  - The Cox-Ingersoll-Ross model
  - The Chan-Karolyi-Longstaff-Sanders (CKLS) family of models
  - The modified CIR and hyperbolic processes
  - The hyperbolic processe
  - The nonlinear mean reversion Ait-Sahaliamodel
  - Double-well potential
  - The Jacobi diffusion process
  - Ahn and Gao model or inverse of Feller's square root model
  - Rarial Ornstein-Uhlenbeck process
  - Pearson diffusions
  - Another classification of linear stochastic systems
  - One epidemic model
  - The stochastic cusp catastrophe model
  - Exponential families of diffusions
  - Generalized inverse gaussian diffusions