---
title: "球面の変形〜Rで学ぶ曲面の四元数共形変換"
author: "ryamada"
date: "Saturday, April 04, 2015"
output: html_document
---
```{r}
library(onion) # 四元数
library(geometry) # 3次元ベクトル・クロス積関数
library(Matrix) # 疎行列
library(rgl) # 3Dプロット
library(knitr) # 文書作成・画像埋め込み
library(igraph) # グラフ理論
```
北極から南極まで、等緯度間隔で球を輪切りにする。
各輪切りには、等経度間隔の点を取る。点間距離が、緯度経度の全体で同じくらいになるように、配置数を調節する。
同一緯線上の点には周回するように辺を置き、
隣接緯線上の点には、橋渡しの辺が経線方向に近くなるように配置し、三角化する。
引数
n.psiは単位球の緯度の刻み数。北極-南極の両端を含めてn.psi段
出力
xyz 頂点3次元座標
edge 三角形の辺の両端頂点ID 2列の行列
triangles 三角形の3頂点ID 3列の行列
以下に実装した関数を示し、それを用いた、球面三角形メッシュと、三角形タイル敷きつめの図を表示する。
```{r}
my.sphere.tri.mesh <- function(n.psi=30){
thetas <- list()
psis <- seq(from=-pi/2,to=pi/2,length=n.psi)
d.psis <- psis[2]-psis[1]
hs <- sin(psis)
rs <- sqrt(1-hs^2)
ls <- 2*pi*rs
n.thetas <- floor(ls/d.psis)
thetas[[1]] <- c(2*pi)
for(i in 2:(n.psi-1)){
thetas[[i]] <- seq(from=0,to=2*pi,length=n.thetas[i]+1)
thetas[[i]] <- thetas[[i]][-(n.thetas[i]+1)]
}
thetas[[n.psi]] <- c(2*pi)
sapply(thetas,length)
bridge <- list()
for(i in 1:(n.psi-1)){
a <- c(thetas[[i]],2*pi)
b <- c(thetas[[i+1]],2*pi)
bridge[[i]] <- matrix(c(1,1),1,2)
loop <- TRUE
while(loop){
n.r <- nrow(bridge[[i]])
id.a <- bridge[[i]][n.r,1] + 1
id.b <- bridge[[i]][n.r,2] + 1
if(id.a > length(thetas[[i]]) & id.b > length(thetas[[i+1]])){
if(id.a-1!=1 & id.b-1!=1){
bridge[[i]] <- rbind(bridge[[i]],c(1,id.b-1))
}
loop <- FALSE
}else{
if(id.a > length(thetas[[i]])){
tmp <- c(id.a-1,id.b)
}else if(id.b > length(thetas[[i+1]])){
tmp <- c(id.a,id.b-1)
}else{
if(a[id.a] < b[id.b]){
tmp <- c(id.a,id.b-1)
}else{
tmp <- c(id.a-1,id.b)
}
}
bridge[[i]] <- rbind(bridge[[i]],tmp)
}
}
}
xyz <- matrix(0,0,3)
edge <- matrix(0,0,2)
triangles <- matrix(0,0,3)
n.triangles <- rep(0,n.psi-1)
for(i in 1:n.psi){
n.r <- nrow(xyz)
if(i > 1){
pre <- (n.r-length(thetas[[i-1]])+1):n.r
post <- (n.r+1):(n.r+length(thetas[[i]]))
edge <- rbind(edge,cbind(post,c(post[-1],post[1])))
br <- bridge[[i-1]]
new.edge <- cbind(pre[br[,1]],post[br[,2]])
edge <- rbind(edge,new.edge)
tmp.tri <- cbind(new.edge,rbind(new.edge[-1,],new.edge[1,]))
tmp <- apply(tmp.tri,1,unique)
triangles <- rbind(triangles,t(tmp))
n.triangles[i-1] <- length(tmp[1,])
}
psi <- psis[i]
theta <- thetas[[i]]
xyz <- rbind(xyz,cbind(cos(psi) * cos(theta),cos(psi)*sin(theta),sin(psi)))
}
return(list(xyz=xyz,edge=edge,triangles=triangles,n.psi=n.psi,thetas=thetas,n.triangles=n.triangles))
}
```
```{r setup}
knit_hooks$set(rgl = hook_rgl)
```
```{r}
n.psi <- 15
sp.mesh <- my.sphere.tri.mesh(n.psi)
```
```{r,rgl=TRUE}
plot3d(sp.mesh$xyz)
segments3d(sp.mesh$xyz[c(t(sp.mesh$edge)),])
```
```{r,rgl=TRUE}
plot3d(sp.mesh$xyz)
mesh.tri <- tmesh3d(t(sp.mesh$xyz),t(sp.mesh$triangles),homogeneous=FALSE)
shade3d(mesh.tri,col="gray")
```
3次元座標を四元数の虚部の3要素に対応付けることで、座標の操作・ベクトル計算が容易になるので、四元数表現を取り入れる。
onionパッケージのHi,Hj,Hkはそれぞれ四元数虚部3軸の単位元に相当する。
```{r}
vertices.mat <- t(sp.mesh$xyz) # 3行行列化
# 座標を純虚四元数化
vertices <- vertices.mat[1,]*Hi + vertices.mat[2,]*Hj + vertices.mat[3,]*Hk
edges <- sp.mesh$edge
faces.v <- t(sp.mesh$triangles)
n.v <- length(vertices) # 頂点数
n.f <- length(faces.v[1,]) # 三角形数
```
曲率的な値rho(実数)を頂点・三角形に与える。
実装にあたっては、頂点にrho値を定義し、
三角形が表す小領域のrho値は、三頂点のrho値の算術平均とする。
以下のRコマンドによる初期化は、各オブジェクトが実数であるのか、四元数であるのか、ベクトルであるのか、行列であるのか、そのサイズはいくつなのかをわかりやすくすることを目的としている。
たとえば、rho.vは頂点のrho値を持つベクトルで、その初期値は実数としての0であり、長さは、頂点数n.vである、と示してある。
同様に三角形のrho値、rho.f (f:face)は、三角形数n.f個の要素の実ベクトルである。
```{r}
rho.v <- rep(0,n.v) # 頂点における
rho.f <- rep(0,n.f) # 三角形における
# 関数 rho.fromVtoTri()は後掲
#rho.f <- rho.fromVtoTri(rho.v,faces.v)
```
曲面の各所にrhoに近い値を取りつつ、それが、単位球面からの共形変換であるようにしたい。
そのような変換では、各点に局所回転を定め、その局所回転が滑らかに移行することである。
その理由は、曲面の共形変換とは、局所に回転を定めることであるから。
この点については、本書では詳述しない。
また、三次元空間座標の回転は、四元数とその共役とで挟んだ積であることから、各点に局所回転を定めることは、各点に四元数を定めることである。
四元数における三次元空間座標回転についても、詳述しない。
共形変換と別の共形変換との移行関係は簡単なので、とりあえずの共形変換〜局所回転〜が定まればよい。
そのために、曲面の座標・三角メッシュ・三角形のrhoから作られる頂点数x頂点数の四元数行列Eを作る。
四元数行列は実、i,j,k要素ごとに頂点数x頂点数の長さの疎ベクトルとして作成し、そこから(頂点数x4)x(頂点数x4)の実行列版E.reを作成する。
ここで言う、疎ベクトルはMatrixパッケージが提供する、疎ベクトル・疎行列オブジェクトのそれである。
疎ベクトル・疎行列オブジェクトでは、0の多いベクトル・行列の場合に、非0値とその番地を情報として把持することで、メモリを節約し、そのようなデータの持ち方をしながら、線形代数演算を効率に行えるような関数を実装することで、大型ながら疎な行列の演算が可能となっている。
以下の例では、初期疎ベクトルとして、値0を第i=1番地に持つ、長さが頂点数の二乗であるようなベクトルである。
```{r}
E <- list(rep(sparseVector(c(0),i=c(1),length=n.v^2),4))
E.re <- matrix(0,n.v*4,n.v*4)
# 関数 my.make.E.v()は後掲
# E <- my.make.E.v(vertices,faces.v,rho.f)
# 関数 my.qMtorM()は後掲
# E.re <- my.qMtorM(E)
```
Eの固有ベクトルの一つを近似的に求めるにあたり、逆冪乗法を用いる。
そのようにして求めた近似解がlambda.vである。(頂点数x4)x(頂点数x4)の実行列の固有ベクトルであり、長さが(頂点数x4)の実ベクトルである。
行列Eを頂点数x頂点数の四元数行列であると考えれば、得られる固有ベクトルは頂点数の長さの四元数ベクトルである、ともみなせる。
逆冪乗法では、適当な初期ベクトルx0を与え、Ax1=x0を解き、次いでAx2=x1を解くという手順を繰り返す。
繰り返し数はそれほど多くなくても収束がよいことが知られているので、3回繰り返しをデフォルトとして採用している。
```{r}
lambda.v <- rep(0,n.v*4) # 四元数ベクトルを長さが4倍の実ベクトルとして表したもの
# lambda.v <- rep(0*Hi,n.v) # 四元数ベクトル
# lambda.v <- my.inv.pow.2(E.re)[[1]]
```
Lは曲面の定義情報(頂点座標と三角形メッシュ情報)とから定まる曲面の広がりを表した頂点数x頂点数の実行列。
変形後の頂点座標(純虚四元数)を最小二乗法で推定するにあたり、実行列の各要素を実部のみの四元数と見立てて、(頂点数x4)x(頂点数x4)の実行列L.reに変換し、L x = omega をxについて解くことで、変形後頂点座標を得る。
omegaは各点に推定した回転相当の四元数のベクトルを用いて算出される、四元数ベクトル。
```{r}
L <- matrix(0,n.v,n.v)
L.re <- matrix(0*Hi,n.v*4,n.v*4)
# 関数 my.make.L(),my.make.quatL()は後掲
# L <- my.make.L(vertices,faces.v)
# L.q <- my.make.quatList(L)
# L.re <- my.qMtorM(L.q)
omega <- rep(0*Hi,n.v)
# 関数 my.make.omega()は後掲
# omega <- my.make.omega(vertices,faces.v,lambda.v)
new.vertices <- rep(0*Hi,n.v)
# new.vertices <- as.quaternion(matrix(solve(L.re,omega),nrow=4))
```
入力は頂点座標vertices、頂点が作る三角形メッシュfaces.v、曲がり方情報rhoの3つ。
出力は、変形後頂点座標のnew.vertices。
中間オブジェクトは、固有ベクトルの元となる行列Eが3入力オブジェクトから作成され、それから一意な解(最小固有値に対応する固有ベクトル)の近似解lamdaが得られる。
もう一つの中間オブジェクトはラプラシアン行列で、vertices,faces.vの2つから作成される。
さらなる下流の中間オブジェクトはomegaで、これは、vertices,faces.v,lambdaから算出するが、lambda自体がvertices,faces.vから作成されているから、omegaはlambdaを介してvertices,faces.v,rhoから作成されるものである。
最終出力は、vertices,faces.vのみから作成されるLと、rhoも加わって作成されるomegaとの2つから算出される。
```{r}
lab <- c("v","f","rho","L","E","lmd","omg","n.v")
edge.list <- matrix(c("v","L","f","L","v","E","f","E","rho","E","E","lmb","v","omg","f","omg","lmb","omg","L","n.v","omg","n.v"),byrow=TRUE,ncol=2)
g.rel <- graph.edgelist(edge.list)
plot(g.rel)
```
以下、関数ソースを記しながら、若干のコメントを加えておく。
```{r}
# 頂点のrho値から面のrho値を算出する
rho.fromVtoTri <- function(rho.v,faces.v){
tmp.rho <- matrix(rho.v[faces.v],nrow=3)
apply(tmp.rho,2,mean)
}
# Utility 関数
# 特に疎行列において、面単位で不定回数の値加算をするためのユーティリティ関数
my.vector.access <- function(v,a,func=sum,zero=0){
if(is.vector(v)){
v <- matrix(v,ncol=1)
}
ord <- order(a)
rle.out <- rle(a[ord])
num.row <- length(rle.out[[1]])
num.col <- max(rle.out[[1]])
tmp1 <- rep(1:num.row,rle.out[[1]])
tmp2 <- c()
for(i in 1:num.row){
tmp2 <- c(tmp2,1:rle.out[[1]][i])
}
addr <- tmp1 + num.row*(tmp2-1)
ret.v <- matrix(0,num.row,ncol(v))
for(i in 1:ncol(v)){
if(zero==0){
tmp.V <- sparseVector(v[ord,i],i=addr,length=num.row*num.col)
M <- Matrix(tmp.V,num.row,num.col)
}else{
M <- matrix(zero,num.row,num.col)
M[addr] <- v[ord,i]
}
ret.v[,i] <- apply(M,1,func)
}
return(list(A = rle.out[[2]],V = ret.v))
}
my.make.E.v <- function(vertices,faces.v,rho){
edge1 <- vertices[faces.v[2,]]-vertices[faces.v[1,]]
edge2 <- vertices[faces.v[3,]]-vertices[faces.v[1,]]
tmp <- edge1 * edge2
A <- abs(i(tmp)+j(tmp)+k(tmp))/2
coef.a <- -1/(4*A)
coef.b <- rho/6
coef.c <- A*rho^2/9
E.re <- E.i <- E.j <- E.k <- sparseVector(c(0),i=c(1),length=length(vertices)^2)
e.q <- list()
e.q[[1]] <- vertices[faces.v[2,]]-vertices[faces.v[3,]]
e.q[[2]] <- vertices[faces.v[3,]]-vertices[faces.v[1,]]
e.q[[3]] <- vertices[faces.v[1,]]-vertices[faces.v[2,]]
for(i in 1:3){
for(j in 1:3){
tmp <- coef.a * e.q[[i]] * e.q[[j]]+ coef.b * (e.q[[j]] -e.q[[i]] ) + coef.c
addr <- faces.v[i,] + (length(vertices)*(faces.v[j,]-1))
tmp.v <- t(as.matrix(tmp))
tmp.out <- my.vector.access(tmp.v,addr)
E.re <- E.re + sparseVector(tmp.out[[2]][,1],tmp.out[[1]],length(vertices)^2)
E.i <- E.i + sparseVector(tmp.out[[2]][,2],tmp.out[[1]],length(vertices)^2)
E.j <- E.j + sparseVector(tmp.out[[2]][,3],tmp.out[[1]],length(vertices)^2)
E.k <- E.k + sparseVector(tmp.out[[2]][,4],tmp.out[[1]],length(vertices)^2)
}
}
return(list(E.re=E.re,E.i=E.i,E.j=E.j,E.k=E.k))
}
my.qMtorM <- function(Es){
n <- sqrt(length(Es[[1]]))
N <- (n*4)^2
init.id <- c(1:4,(1:4)+n*4,(1:4)+n*4*2,(1:4)+n*4*3)
spacing.id <- c(outer((0:(n-1)*4),n*4*4*(0:(n-1)),"+"))
ret <- sparseVector(c(0),i=c(1),N)
a <- c(1,2,3,4,2,1,4,3,3,4,1,2,4,3,2,1)
b <- c(1,1,1,1,-1,1,1,-1,-1,-1,1,1,-1,1,-1,1)
for(j in 1:length(a)){
tmp.v <- sparseVector(b[j] * Es[[a[j]]]@x,i=init.id[j]+spacing.id[Es[[a[j]]]@i],length=N)
ret <- ret + tmp.v
}
Matrix(ret,n*4,n*4)
}
my.inv.pow.2 <- function(A,n.iter=3,b=rep(1,ncol(A)),log=FALSE){
x <- b
if(log){
x.log <- matrix(0,n.iter+1,ncol(A))
x.log[1,] <- x
}
for(i in 1:n.iter){
x2 <- solve(A,x)
x <- x2/sqrt(sum(x2^2))
if(log){
x.log[i+1,] <- x
}
}
if(log){
return(list(x=x,x.log=x.log))
}else{
return(list(x=x,x.log=matrix(0,0,ncol(A))))
}
}
my.make.L <- function(vertices,faces.v){
n.v <- length(vertices)
L <- sparseVector(c(0),i=c(1),length=n.v^2)
for(i in 1:3){
v.ord <- ((1:3)+i+1) %% 3 + 1
k1 <- faces.v[v.ord[1],]
k2 <- faces.v[v.ord[2],]
k3 <- faces.v[v.ord[3],]
v1 <- vertices[k1]
v2 <- vertices[k2]
v3 <- vertices[k3]
u1 <- v2-v1
u2 <- v3-v1
u12 <- u1 * u2
cotAlpha <- (-Re(u12))/Mod(Im(u12))
addrk2k2 <- k2 + (k2-1)*n.v
addrk3k3 <- k3 + (k3-1)*n.v
addrk2k3 <- k2 + (k3-1)*n.v
addrk3k2 <- k3 + (k2-1)*n.v
addr <- c(addrk2k2,addrk3k3,addrk2k3,addrk3k2)
val <- c(cotAlpha,cotAlpha,-cotAlpha,-cotAlpha)/2
tmp.out <- my.vector.access(val,addr)
L <- L + sparseVector(tmp.out[[2]][,1],tmp.out[[1]],n.v^2)
}
L
}
my.make.quatList <- function(L){
L.q <- list()
L.q[[1]] <- L
for(i in 2:4){
L.q[[i]] <- L*0
}
L.q
}
my.make.omega <- function(vertices,faces.v,lambda){
n.v <- length(vertices)
omega <- rep(0*Hi,n.v)
for(i in 1:3){
v.ord <- ((1:3)+i+1) %% 3 + 1
k1 <- faces.v[v.ord[1],]
k23 <- rbind(faces.v[v.ord[2],],faces.v[v.ord[3],])
k23 <- apply(k23,2,sort)
k2 <- k23[2,]
k3 <- k23[1,]
v1 <- vertices[k1]
v2 <- vertices[k2]
v3 <- vertices[k3]
edge <- v3-v2
lambda.mat <- matrix(lambda,nrow=4)
lambda.q <- as.quaternion(lambda.mat)
lambda.mat.2 <- lambda.mat
lambda.mat.2[2:4,] <- -lambda.mat.2[2:4,]
lambda.q. <- as.quaternion(lambda.mat.2)
lambda1 <- lambda.q[k2]
lambda1. <- lambda.q.[k2]
lambda2 <- lambda.q[k3]
lambda2. <- lambda.q.[k3]
val <- 1/3 * lambda1. * edge * lambda1 + 1/6 * lambda1. * edge * lambda2 + 1/6 * lambda2. * edge * lambda1 + 1/3 * lambda2. * edge * lambda2
u1 <- v2-v1
u2 <- v3-v1
u12 <- u1 * u2
cotAlpha <- (-Re(u12))/Mod(Im(u12))
Val <- cotAlpha * val /2
Val.m <- t(as.matrix(Val))
tmp.out2 <- my.vector.access(-Val.m,k2)
tmp.out3 <- my.vector.access(Val.m,k3)
omega[tmp.out2[[1]]] <- omega[tmp.out2[[1]]] + as.quaternion(t(tmp.out2[[2]]))
omega[tmp.out3[[1]]] <- omega[tmp.out3[[1]]] + as.quaternion(t(tmp.out3[[2]]))
}
omega.re <- as.matrix(omega)
omega.re <- omega.re-apply(omega.re,1,mean)
c(omega.re)
}
```
# 球面的曲面の変換
曲面の三角化が定まっており、その
初期頂点座標が与えられ、その各頂点にrhoが働くものとして、関数を作る。
```{r}
my.conformal.rho <- function(vertices,faces.v,rho.v){
xyz.ori <- t(as.matrix(vertices)[2:4,])
n.v <- length(vertices) # 頂点数
n.f <- length(faces.v[1,]) # 三角形数
rho.f <- rho.fromVtoTri(rho.v,faces.v)
E <- my.make.E.v(vertices,faces.v,rho.f)
E.re <- my.qMtorM(E)
lambda.v <- my.inv.pow.2(E.re)[[1]]
L <- my.make.L(vertices,faces.v)
L.q <- my.make.quatList(L)
L.re <- my.qMtorM(L.q)
omega <- my.make.omega(vertices,faces.v,lambda.v)
new.vertices <- as.quaternion(matrix(solve(L.re,omega),nrow=4))
xyz.new <- t(as.matrix(new.vertices)[2:4,])
mean.new <- apply(xyz.new,2,mean)
xyz.new. <- t(t(xyz.new)-mean.new)
max.new. <- max(abs(xyz.new.))
xyz.new.st <- xyz.new./max.new.
#ret <- xyz.new.st[,1]*Hi + xyz.new.st[,2]*Hj + xyz.new.st[,3]*Hk
ret <- list(xyz.new=xyz.new.st,xyz.ori=sp.mesh$xyz,xyz.new.q=new.vertices,xyz.ori.q=vertices,faces.v=faces.v,E=E,L=L,lambda.v=lambda.v,omega=omega,n.psi=n.psi,rho.fx=rho.fx,rho.v=rho.v,rho.f=rho.f,sp.mesh=sp.mesh)
ret
}
```
単位球面上の点にrho.vを与える関数を定め、適当な球面点密度をn.psiで指定した上で、上述の各種オブジェクトを作成する関数を作る
```{r}
my.sphereConformal <- function(n.psi,rho.fx){
sp.mesh <- my.sphere.tri.mesh(n.psi)
vertices.mat <- t(sp.mesh$xyz) # 3行行列化
vertices <- vertices.mat[1,]*Hi + vertices.mat[2,]*Hj + vertices.mat[3,]*Hk
edges <- sp.mesh$edge
faces.v <- t(sp.mesh$triangles)
rho.v <- rho.fx(sp.mesh$xyz) # 頂点における
out <- my.conformal.rho(vertices,faces.v,rho.v)
ret <- list(xyz.new=out$xyz.new,xyz.ori=sp.mesh$xyz,xyz.new.q=out$new.vertices,xyz.ori.q=vertices,faces.v=faces.v,E=out$E,L=out$L,lambda.v=out$lambda.v,omega=out$omega,n.psi=n.psi,rho.fx=rho.fx,rho.v=rho.v,rho.f=out$rho.f,sp.mesh=sp.mesh)
ret
}
plot.sp.conformal <- function(xyz,faces.v,sp.tri,rho.f,col1=c(4,5)){
plot3d(xyz,xlab="x",ylab="y",zlab="z")
mesh.tri <- tmesh3d(t(xyz),faces.v,homogeneous=FALSE)
col. <- rep(col1,length(sp.tri))[1:length(sp.tri)]
col <- rep(col.,sp.tri*3)
rho.f <- rep(rho.f,each=3)
rho.f <- (rho.f-min(rho.f))/(max(rho.f)-min(rho.f))
col2 <- rgb(1,1-rho.f,col/6)
shade3d(mesh.tri,col=col2)
}
```
適当なrhoで曲げてみる
```{r}
rho.fx <- function(X){
ret <- sin(X[,1]*pi*2 )*1
return(ret)
}
n.psi <- 40
out <- my.sphereConformal(n.psi,rho.fx)
```
同じ緯度からの変形がわかるように、縞をつけつつ、rho値の勾配をつけてプロットする。
変形前。
```{r,rgl=TRUE}
plot.sp.conformal(out$xyz.ori,out$faces.v,out$sp.mesh$n.triangles,out$rho.f)
```
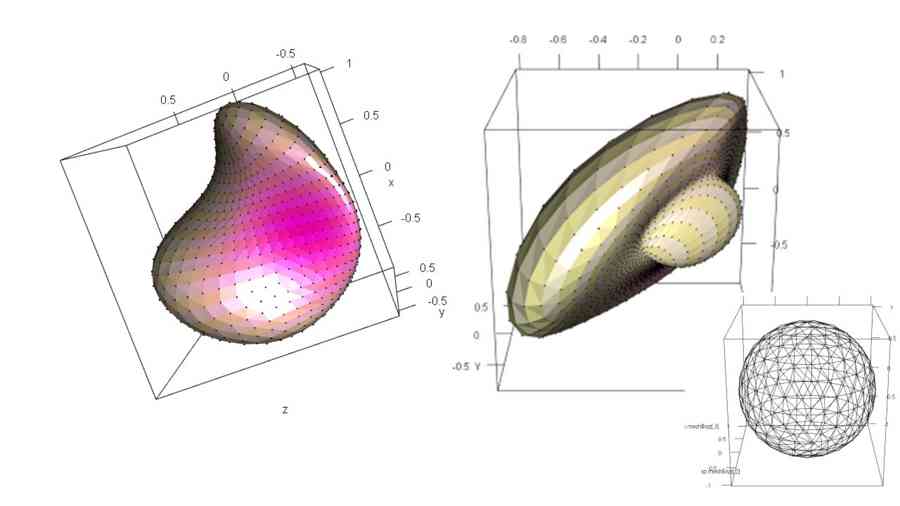
変形後
```{r,rgl=TRUE}
plot.sp.conformal(out$xyz.new,out$faces.v,out$sp.mesh$n.triangles,out$rho.f)
```
