準結晶とリーマン予想 - ryamadaのコンピュータ・数学メモ

昨日の話はおそらく準結晶とリーマン予想に関するこの話につながると思う
- ゼータ関数を０にする値でnon-trivialなものの実数部分は0.5である(リーマン予想)としてその虚数部分のリスト( $K=(k_1,k_2,...)$ )がこちらにある。それを使って…
- $F(x)=\sum_j e^{i k_j x}$ を計算する

non.Trivial.Zero.10000 <- read.table("http://www.dtc.umn.edu/~odlyzko/zeta_tables/zeros1")
zeta.zero <- unlist(non.Trivial.Zero.10000)
x <- seq(from=0,to=15,length=1000)
x <- c(x,log(1:100000))
x <- sort(x)
y <- rep(0,length(x))
for(i in 1:length(zeta.zero)){
	y <- y + exp(1i*zeta.zero[i]*x)
}
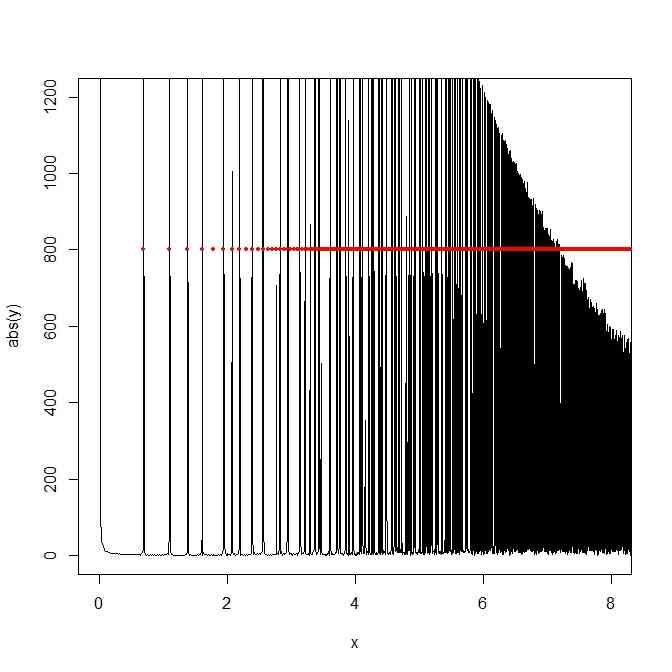
plot(x,abs(y),xlim=c(0,8),ylim=c(0,1200),type="l")
points(log(2:100000),rep(800,99999),pch=20,cex=0.8,col=2)

これは何をやっているのかというと"In math jargon, what Matt did is take the Fourier transform of a sum of Dirac deltas supported at the imaginary parts of the nontrivial Riemann zeta zeros."とのこと
- "supported at the imaginary parts of the nontrivial Riemann zeta zeros"はゼータ関数を0にする実部が0.5のときの虚部の値たち…に関して何かしている、ということ
- 残るは"Fourier transform of a sum of Dirac deltas"
- フーリエ変換は関数 $f(x)$ があったときに、 $g(\xi)=\int_{-\infty}^{\infty}f(x)e^{-2\pi i x \xi} dx$ (ただし $\xi$ は任意の実数
- ディラックのデルタ関数は、ある一つの値で正の値をとり、それ以外では0であり、全体で積分すると1になるような関数。それの"sum"とは、虚部の値 $k_j$ について、逐一正の値をとるような、多ピーク(無限にピーク数があるだろうと考えられている)のインパルス関数
- 今、 $f(x)$ を $x=k_j$ のときに $f(x=k_j)=C$ とし、 $x!=k_j;j=1,2,...$ のときに $f(x)=0$ であるような関数であるということだから、これをフーリエ変換すると $\int_{-\infty}^{\infty} f(x)e^{-2\pi i x \xi}dx$ であるが、 $\int$ とは言え、 $x=k_j$ のときを離散的に足し合わせることに過ぎないので、 $\sum_{j} f(k_j)e^{-2\pi i k_j \xi}$ となる。ここで、すべての $k_j$ について $f(x)$ が同じ値 $t$ だから $\sum_j C e^{-2\pi i k_j \xi}$ となって、これが「虚部」に関するディラック関数の足し合わせのフーリエ変換の形をしていることがわかる