from scipy.fftpack import fft, ifft
# 周期性データを作る
n = 1000 # 点の数
t = np.linspace(-1,1,n) * 5*np.pi # 時刻点
k = 50 # 重ね合わせる周期関数の数
# a cos(bt+c)の係数a,b,c
a = np.random.randn(k)
b = np.random.randn(len(a))
c = np.random.randn(len(a))
# ゼロベクトル
x = np.zeros_like(t)
for i in arange(len(a)) :
x = x + a[i] * cos(t*b[i]+c[i])
# 乱雑項
x = x + np.random.randn(len(t)) * var(x)*0.01
# 順方向離散フーリエ変換
fft.out = fft(x)
# 逆方向離散フーリエ変換
fft.out2 = ifft(fft.out)
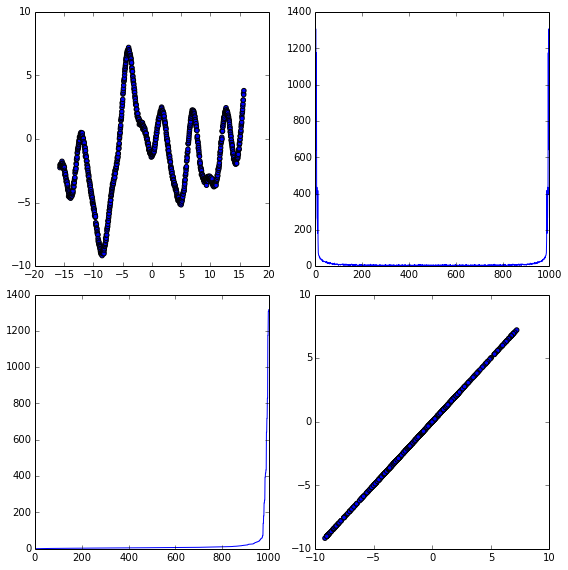
# プロット 2x2=4パネル
mp.pyplot.figure(figsize=(8,8))
mp.pyplot.subplot(2,2,1)
mp.pyplot.scatter(t,x)
mp.pyplot.subplot(2,2,2)
mp.pyplot.plot(abs(fft.out))
mp.pyplot.subplot(2,2,3)
mp.pyplot.plot(sort(abs(fft.out)))
mp.pyplot.subplot(2,2,4)
mp.pyplot.scatter(x,fft.out2)
mp.pyplot.tight_layout()
mp.pyplot.show()
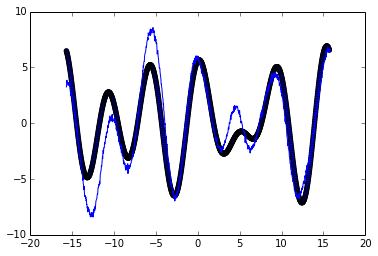
# スペクトル値の絶対値をソートして
mod_out = abs(fft.out)
sort_mod_out = sort(mod_out)
# その上位6番を取り
tmp = sort_mod_out[::-1][]
# 5番までのスペクトルのみを採5用して、他は略す
fft_out_tmp = fft.out
fft_out_tmp[mod_out < tmp] = 0
fft_out2_2 = ifft(fft_out_tmp)
mp.pyplot.plot(t,x)
mp.pyplot.scatter(t,fft_out2_2)
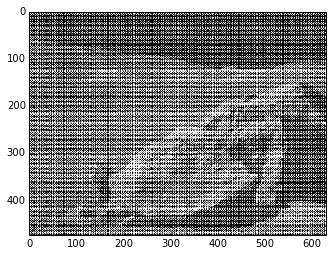
# 読み込む
img_read = mp.pyplot.imread('moonlanding.png')
# Ipython内で表示する
mp.pyplot.imshow(img_read, cmap=mp.pyplot.cm.gray, interpolation='nearest')
# アレイになっている
img_read.shape
# 二次元用fft,ifft関数を使う
from scipy.fftpack import fft2, ifft2
# 二次元離散フーリエ
img_fft2 = sp.fftpack.fft2(img_read)
# こんなんやってもスペクトルがわかりやすく出るわけではない
mp.pyplot.imshow(abs(img_fft2), cmap=mp.pyplot.cm.gray, interpolation='nearest')
# 絶対値でプロット
mp.pyplot.plot(sort(abs(img_fft2)))
# 妙に周期性のあるノイズ周波数成分を除去する
img_fft2[np.where(abs(img_fft2) > 6000)] = 0
# 逆フーリエする
img_fft2_i = sp.fftpack.ifft2(img_fft2)
# 表示する
mp.pyplot.imshow(real(img_fft2_i), cmap=mp.pyplot.cm.gray, interpolation='nearest')