ゼータ関数虚部のディラックデルタ関数のフーリエ変換と素数べき(Prime power)

• 前の記事でゼータ関数の複素数解の虚部のディラックデルタ関数のフーリエ変換でピークが出て来るのを確かめた
• 2,3,4=2^2,5,7,8=2^3,0=3^2,11,13,16=2^4...の対数にピークがあるように見える
• 素数と素数のべきとの対数にピークがある、ということになる。素数と素数のべきというのはPrime Powerと呼ばれる
• 「素数」が数の素(もと)とすると、『もと』そのものと、『単一のもと』から作られる「ピュア」な数ということになるが、それが現れる、ということである
• たしかにPrime Powerが現れているのかどうかを確認してみる
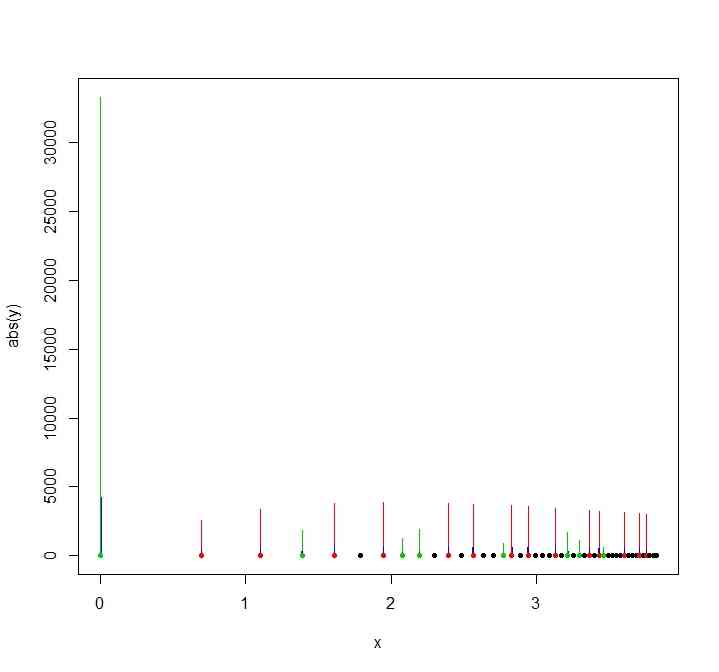
  • たしかにPrime Powerがピークとして残っているけれど、素数そのもの(赤)と比べると素数でない素数べき(緑)のピークは低いのではないだろうか…これらは複素数解虚部の数を増やすと消滅する？それとも消滅しないとしても、p^nのときnが小さい方がピークが高い、というようなルールはあるのでは？

# ゼータ関数解の虚部のリストを取ってくる
non.Trivial.Zero.10000 <- read.table("http://www.dtc.umn.edu/~odlyzko/zeta_tables/zeros1")
zeta.zero <- unlist(non.Trivial.Zero.10000)
# Nまでの素数を取り出す
library(numbers)
N < -100
piN <- Primes(N)
# Prime Powerであるというのは、素因数分解したときの因子が１種類ということなので、1:Nについてそうなっているかの確認をする
powerPrime <- rep(0,N)
for(i in 1:N){
	if(length(table(factorize(i)))==1){
		powerPrime[i] <- 1
	}
}
# 自然数の対数のところにピークが現れるかどうかが知りたいので、その値についてフーリエ変換後の関数値を求めることとする
# その上で、図にしたときにわかりやすいように、「素数」「素数のべきだが素数でない」「それ以外」に色分けする
x <- c(log(1:N))
col <- rep(1,N)
col[which(powerPrime==1)] <- 3
col[piN] <- 2
col.int <- col
# 次に、ピークのごく近傍では、たしかにフーリエ変換後の関数値がほとんど0になっていないと、「パルス」が生じていることにはならないので、各自然数の対数の前後にもフーリエ変換後の関数値を計算することとする
# 関数値を計算したいxの値をソートしてハンドリング上わかりやすくするとともに
# 自然数の対数の前後の値にも別の色を指定する
x <- c(x,x+10^(-3),x-10^(-3))
x <- x[which(x>=0)]
ord <- order(x)
x <- x[ord]
col <- c(col,rep(4,length(x)-N))
col <- col[ord]
# フーリエ変換に使う虚数部の値を一つずつ増やしながらプロットする
# 赤は『素数』の対数→ピークが出るはず
# 緑は『素数以外の素数べき』の対数→ピークが出るはず
# 黒は『素数べき以外の自然数』の対数→0になるはず
# 青は『自然数の対数の前後の値』→0になるはず
# また、『自然数の対数』で0になっているのは、黒であって、赤と緑ではそうならないことを示すために、『自然数の対数』のy軸0のところにそれぞれの色の点を打ってある
y <- rep(0,length(x))
for(i in 1:length(zeta.zero)){
	y <- y + exp(1i*zeta.zero[i]*x)
	plot(x,abs(y),type="h",col=col)
	points(log(1:N),rep(0,N),pch=20,cex=1,col=col.int)
}