2012-07-11

周期的定常状態

MIKU 同期定常楕円

メトロノームが同期する話
その前にメトロノームのこと
メトロノームは振り子のようなもの
一定時間ごとに振れる器具
放っておくと、止まってしまうのでネジを巻いて「カツ」を入れる
そのときの振り子の位置を表す角と角の時間微分とを楕円で近似する(これは理想振り子？）
本当の振り子(メトロノーム)はブランコをこぐように、振れる途中で「力」を入れる
そのときの角と角の時間微分とを2軸に取った軌道は楕円から少しずれる
この歪みの入った軌道や、ネジが切れて、放っておくととまってしまうときの軌道などをRで書いてみようか、という話
$\frac{(\theta(t)^2)}{a^2}+\frac{(\frac{d \theta}{dt})^2}{b^2}=1;a,b > 0$ より
$\theta(t) = a \cos(kt+\delta),\frac{d\theta}{dt} = b \sin(kt + \delta)$
ここで $\delta=0$ と置いても一般性を失わない
その上で $t=0$ のときに $\theta(t=0)$ の符号と $\frac{d \frac{d \theta}{dt}}{dt}$ の符号が逆であるという条件があるから $a,b > 0, k < 0$

a <- 1
b <- 2
k <- -1
t <- seq(from = 0, to = 1, length = 1000) * 2 *pi
theta <- a * cos(k*t)
D.theta <- b * sin(k*t)
matplot(cbind(theta,D.theta),type="l")
plot(theta,theta.,type="l",xlim = range(c(theta,D.theta)),ylim = range(c(theta,D.theta)))

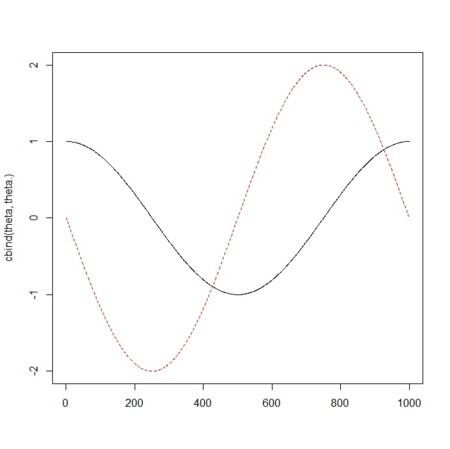
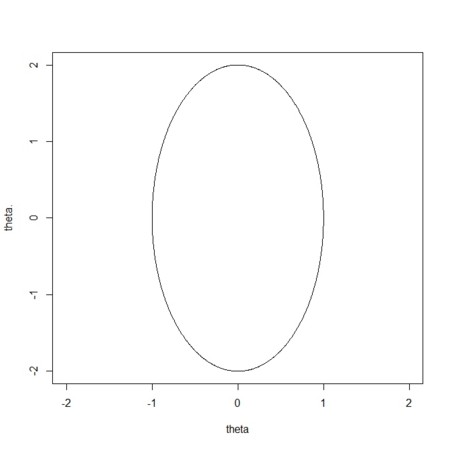
ずれを入れてみる
- 本とは少し変えた設定にしてみる
- $\theta=\theta_{MAX}$ の状態からの変化にあたって、「摩擦」があるために理想よりも遅れがちになりつつ、途中からは、それを補てんする力が働いて、キャッチアップする、とみなす
- このときの角の時間変化を、 $\theta.1(t)$ とすれば、 $\theta.1(t) = \theta(t-\delta(t))$ のように、理想的な場合でならば小さい $t$ のときの位置をとりつつ、 $\theta=-\theta_{MAX}$ のときには、 $\delta(t)$ の項が解消されて $0$ になる
- したがって、 $\delta(t)$ は振れ幅の絶対値が最大のときに0で、それ以外のときは正であるような関数である
- そのような関数としてを使うことにすれば
  - もっと扱いやすくするために、 $\delta(t) = (p\times \sin(kt))^2$ とするとよい(微分とかしやすい)→後半に書き直し
- $\theta.1(t) = \theta(t-|p\times \sin(kt)|)$ であるから
- $\theta.1(t) = a \cos(k(t-|p\times \sin(kt)|))$
- ここで、角の時間変化に同様の時刻遅れを入れるだけで、『位置＝積分(速度)』の関係を守れるのかどうか不安だが、そうしてしまうとすると
まず、時間遅れの様子

p <- 0.5
t.1 <- t - p * abs(sin(k*t))
plot(t,t.1)

次いで、角変化、角速度時間変化は

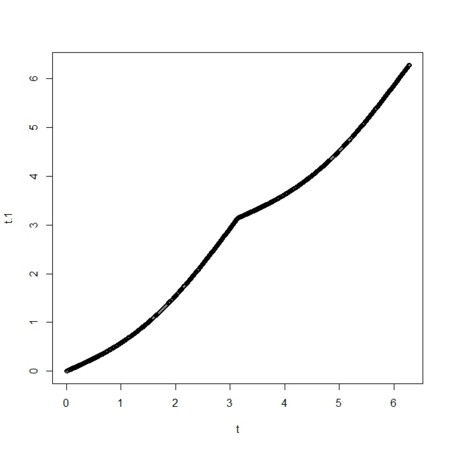
theta.1 <- a * cos(k * t.1)
D.theta.1 <- b * sin(k *t.1)


xlim <- ylim <- range(c(theta.1,D.theta.1))
matplot(cbind(theta,D.theta,theta.1,D.theta.1),type="l")

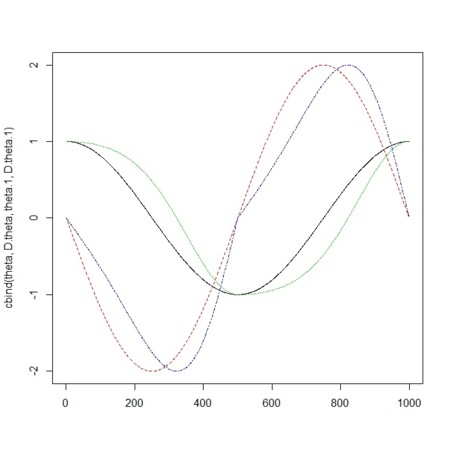
時間遅れ入りの場合の角変化と角速度変化の関係は、相変わらず楕円で

plot(theta.1,D.theta.1,type="l",xlim = xlim,ylim = ylim)

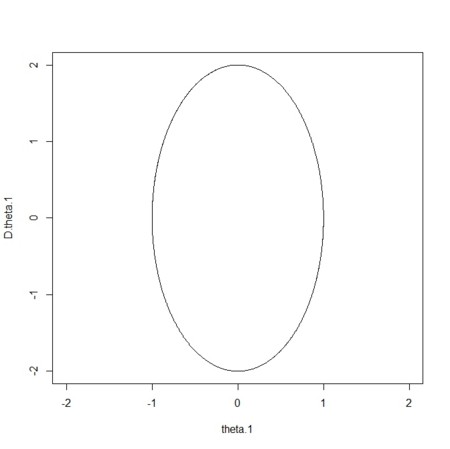
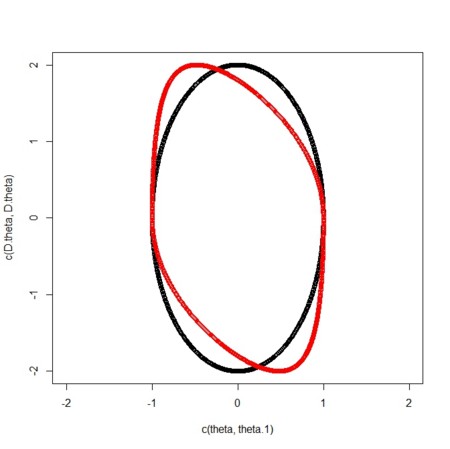
あえて、「元の」角変化と遅れ入りの角速度変化を組み合わせると、楕円のゆがみを作ることができる

plot(c(theta,theta.1),c(D.theta,D.theta),col=rep(1:2,each = length(t)),xlim = xlim,ylim = ylim)

$\delta(t) = (p\times \sin(kt))^2$ で書き直し
$\theta.1(t) = \theta(t-(p\times \sin(kt))^2)$
をで微分すれば
- $\frac{\theta.1(t)}{dt} = -a\sin(k(t-(p\times \sin(kt))^2)) \times k\times(1-2p\times \sin(kt)\cos(kt)$

a <- 1
b <- 2
k <- -1
t <- seq(from = 0, to = 1, length = 1000) * 2 *pi
theta <- a * cos(k*t)
D.theta <- b * sin(k*t)
matplot(cbind(theta,D.theta),type="l")
plot(theta,theta.,type="l",xlim = range(c(theta,D.theta)),ylim = range(c(theta,D.theta)))
p <- 0.2
t.1 <- t - p * abs(sin(k*t))
t.2 <- t - p * (sin(k*t))^2
theta.1 <- a * cos(k * t.1)
D.theta.1 <- b * sin(k *t.1)
theta.2 <- a*cos(k*t.2)
D.theta.2 <- b*sin(k*t - p*(sin(k*t))^2) * (k*(1-2*p*sin(k*t)*cos(k*t)))
plot(t,t.2)

xlim <- ylim <- range(c(theta.2,D.theta.2))
matplot(cbind(theta,D.theta,theta.2,D.theta.2),type="l")
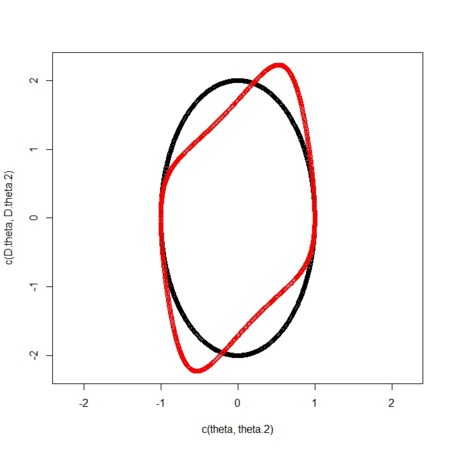
plot(c(theta,theta.2),c(D.theta,D.theta.2),col=rep(1:2,each = length(t)),xlim = xlim,ylim = ylim)

plot(theta.2,D.theta.2,type="l",xlim = xlim,ylim = ylim)