遺伝学・遺伝統計学関連の姉妹ブログ『ryamadaの遺伝学・遺伝統計学メモ』
京都大学大学院医学研究科ゲノム医学センター統計遺伝学分野のWiki
講義・スライド
医学生物学と数学とプログラミングの三重学習を狙う学習ツール
駆け足で読む○○シリーズ
ぱらぱらめくるシリーズ
カシオの計算機
オンライン整数列大辞典

SAGEでリーマンの写像定理遊びをする

SAGE リーマンの写像定理
  • 単位円板と同相な面があったとき、conformalな写像が存在して、単位円板に滑らかに移せる、しかもしれは一意、というのがリーマンの写像定理
  • 存在証明と一意性の証明はされるものの、「みつける」のは面倒くさくて、計算機的にはちまちまと計算するらしい
  • 数学アプリのsageにはそれがあって、最近のsageはjupyter notebookでさらさらとじっこうできる。背後ではpythonのベクトル・行列状データ保持などを使っていることもあり、pythonでやっているようなつもりでできる
  • sageのインストールはこちら

www.sagemath.org
。こちらでもよい

  • さて、立ち上がるようになったら、Riemannの写像定理の実例ページに行ってみよう
  • 絵が出るコードがないと、楽しめないので、例えばこちら

projecteuclid.orgに行ってみよう

  • いろいろあるけれど、多角形にうまいこと単位円板と対応付けられる座標系を描いてくれそうな図とコードがあるのでやってみる
  • インストールしたSAGE-MATHのjupyter版を起動すれば、jupyter notebookが立ち上がるので、あ他らしいノートブックを作る。もちろん、実行カーネルはsage-math
ps = polygon_spline([(-1,-1),(1,-1),(1,1),(-1,1)])
z = lambda t: ps.value(t) # Riemann map for a square
zp = lambda t: ps.derivative(t)
m = Riemann_Map([z],[zp],.3+.3*I)
p = m.plot_colored(plot_points=1000) +m.plot_spiderweb(pts=150)
show(p,axes=false)
  • これをrunしてエラーが出なければOK

f:id:ryamada:20200719100727p:plain

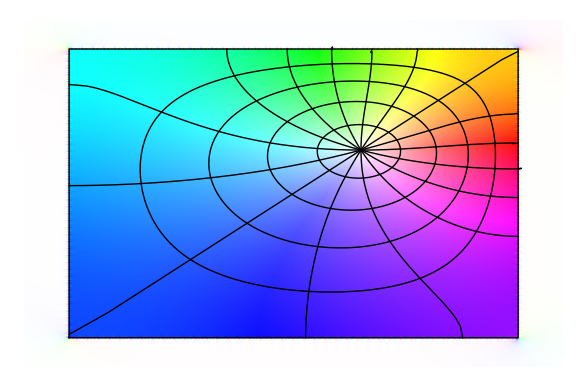
  • このコードが何をしているのかが読みとれれば、改変して使えるはず
ps = polygon_spline([(-1,-1),(1,-1),(1,1),(-1,1)])
  • 多角形とその(内部)のスプライン曲線をいじる関数っぽい。２次元４点を指定している模様であり、それは、出力図とも符合するから、そう信じてよさそう
z = lambda t: ps.value(t) # Riemann map for a square
  • 作った多角形psに何かしら変数tを与えて計算しているっぽい。実際、この変数tはデフォルトで実数値パラメタとして適当な幅等で作るものらしいので、使うことする。zに何かpsの領域に値付けがされたことになる
zp = lambda t: ps.derivative(t)
  • こちらも同様に多角形ps内に値を与える処理らしい。derivativeという用語からわかるように微分と関係しているのだろう。滑らかにしたいし、conformalにしたいから、微分は大事なのでしょう
m = Riemann_Map([z],[zp],.3+.3*I)
  • ここにRiemann_Map()なる、いかにも「本体」な関数が出ている。ps内部に算出した２種類の値 zとzsとを引数として取り、第三の引数 .3 + .3 * I を取っている。これは複素数。図を見ると、座標系の中心を定めた極座標形式の曲線群が描かれているから、その曲線群の「中心」は大事な役割なはずであることがわかる。確かに、第三引数である複素数を複素平面上の点としたときの位置が、曲線群の「起点」になっているから、起点指定をしているのだろうと想像がつく
p = m.plot_colored(plot_points=1000) +m.plot_spiderweb(pts=150)
show(p,axes=false)
  • これは見るからに、プロット。colorに関することと、spiderweb(中心を持った蜘蛛の巣に関することを、点の数で指定しているように読めるから、図の解像度だろうと予想される。色は、複素数の様子を表すためのもの、蜘蛛の巣は、単位円板だったら、射的の的の極座標に相当するもの
  • これで準備は終わり
  • spiderwebの方だけ、もう少し、パラメタ指定を細かくできるようになっておくと便利そうなので、help(m.plot_spiderwb)などで調べておく
  • さあ、本題
  • 適当な多角形でやってみよう
ps = polygon_spline([(0,0),(1,0),(3/2,sqrt(3)/2),(1,sqrt(3)),(0,sqrt(3)),(1/2,sqrt(3)/2)]) # 正三角形の貼り合わせ
z = lambda t: ps.value(t) # Riemann map for正三角形の貼り合わせ
zp = lambda t: ps.derivative(t)
m = Riemann_Map([z],[zp],1.0+sqrt(3)/2*I) # 中心を (1.0, sqrt(3/2)として描く
p = m.plot_colored(plot_points=100) +m.plot_spiderweb(spokes=64, circles=8,pts=30) # 極座標の放射線の数と輪の数を追加指定してみた
show(p,axes=false)

f:id:ryamada:20200719101939p:plain

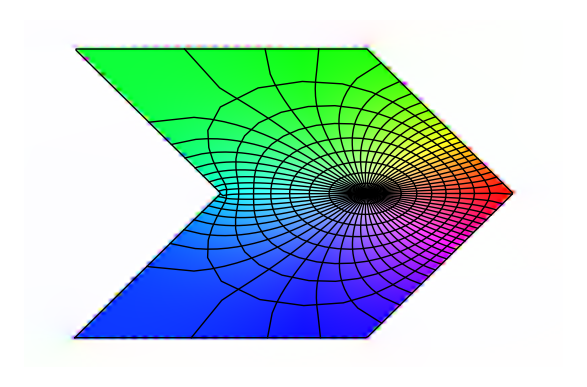
ps = polygon_spline([(0,0),(1,0),(3/2,sqrt(3)/2),(1,sqrt(3)),(0,sqrt(3)),(1/2,sqrt(3)/2)]) # 正三角形の貼り合わせ
z = lambda t: ps.value(t) # Riemann map for正三角形の貼り合わせ
zp = lambda t: ps.derivative(t)
m = Riemann_Map([z],[zp],0.2+0.2*I) # 中心を変えてみた
p = m.plot_colored(plot_points=100) +m.plot_spiderweb(spokes=64, circles=8,pts=150)
show(p,axes=false)
  • 中心を変えると、凹になったところがちょっとうまく行っていない感じ。リーマンの写像定理は、凹凸があってもいけるはずなので、この辺りは、今使っている計算関数の仕様が、そのあたりをはしょっているせいなのかなー、と思われる。詳しくは、計算アルゴリズムの説明に当たらないといけないが、遊びだから良しとしよう

f:id:ryamada:20200719102214p:plain

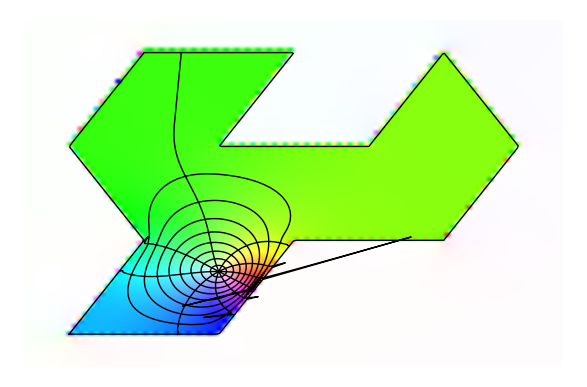
  • さらに形を複雑にすると、spiderwebに無理が生じることがわかり、関数のアルゴリズムが端折っているせいだという予想がさらに高まる…
ps = polygon_spline([(0,0),(1,0),(3/2,sqrt(3)/2),(5/2,sqrt(3)/2),(3,sqrt(3)),(5/2,3*sqrt(3)/2),(2,sqrt(3)),(1,sqrt(3)),(3/2,3*sqrt(3)/2),(1/2,3*sqrt(3)/2),(0,sqrt(3)),(1/2,sqrt(3)/2)]) # 正三角形の貼り合わせ
z = lambda t: ps.value(t) # Riemann map for正三角形の貼り合わせ
zp = lambda t: ps.derivative(t)
m = Riemann_Map([z],[zp],1.0+sqrt(3)/3*I) # 中心を (1.0, sqrt(3/2)として描く
p = m.plot_colored(plot_points=100) +m.plot_spiderweb(spokes=10, circles=8,pts=150)
show(p,axes=false)

f:id:ryamada:20200719102344p:plain

Ptolemy's theorem トレミーの定理

トレミーの定理 Ptolemy 幾何
  • 円に内接する四角形ABCDがあった時|AC|\times |BD| = |AB| \times |CD| + |BC| \times |DA|が成り立つそうだ

en.wikipedia.org

t <- sort(runif(4) * 2 * pi)
x <- cos(t)
y <- sin(t)
xy <- cbind(x,y)
d <- as.matrix(dist(xy))
d

d[1,3] * d[2,4] - (d[1,2] * d[3,4] + d[2,3] * d[4,1])

> t <- sort(runif(4) * 2 * pi)
> x <- cos(t)
> y <- sin(t)
> xy <- cbind(x,y)
> d <- as.matrix(dist(xy))
> d
         1        2        3        4
1 0.000000 0.855728 1.940275 1.976644
2 0.855728 0.000000 1.546143 1.656181
3 1.940275 1.546143 0.000000 0.183788
4 1.976644 1.656181 0.183788 0.000000
> d[1,3] * d[2,4] - (d[1,2] * d[3,4] + d[2,3] * d[4,1])
[1] 4.440892e-16
  • 単位球面上の四角形では成り立たないようだが、双曲面の場合に、単位円板の円周上の点（無限遠点）を頂点とする四角形の場合には、距離の取り方をちゃんとすると成り立つらしい

https://www.maths.gla.ac.uk/wws/cabripages/hyperbolic/hybrid1.html

Teichmuller spaceの座標系

Teichmuller space 座標 Frechel-Nielsen Shear coordinate Shift coordinate Lambda length
  • 特徴づけられた定負曲率面のトポロジー的関係が作るTeichmuller spaceには座標が与えられる
  • 色々な座標がある
  • Wikipediaの記事にも

Coordinatesの項があり、Frechel-Nielsen coordinates, Shear coordinates, Earthquakesが書かれている

  • それ以外にも、文献検索によりTrace coordinatesとかShift coordinatesなども見つかる
  • また、Coordinatesの値を与えるために導入されるLambda lengthsなどの概念も必要になる
  • 元々の「特徴づけられた定負曲率面」が異なるので、それぞれ、うまく機能する座標を入れるには、それぞれに合致したそれを作らないといけない、と言うことなのだろう
  • その上で、三角化メッシュのための座標系を理解することを目標にしつつ、それ以外の座標系にも目配りして、Teichmuller spaceの座標系をより整理した形で理解できれば、と思ってこの記事を書く
  • Teichmuller 座標とは違うが、曲面上のarc同士の関係には、intersection number(交叉回数)と言うものがある。これは、arcを団変数とした時に、そのローラン多項式の分母に相手方arc変数の次数と一致する

三角化のTeichmuller spaceのための基礎

  • https://ryamada.hatenadiary.jp/entry/20200705/1593907656:こちらの記事で、genus 穴のある閉曲面特徴づけとしてTeichmuller spaceの基礎事項をまとめた
  • 今回の記事は、閉曲面の三角メッシュの線の引き具合のTeichmuller spaceを考えるための基礎事項をまとめておく
  • そもそも、閉曲面の三角メッシュがTeichmuller spaceの対象となる、とはどういうことか。。。
    • 三角メッシュは、平面グラフであるから、「ある辺」を連続的に動かしても良いけれど、他の辺と交叉してはいけない、というルールの下で同一視することにすれば、閉曲面上にある数の点をおいた時に、そこに作れる三角メッシュのパターンは、位相的な情報になる
  • 結局、三角化を位相的に捉えてTeichmuller spaceで扱う時に問題とする情報は：
    • 閉曲面のgenus
    • 閉曲面上の点の数
  • 普通の三角メッシュと一般化した三角メッシュ
    • いわゆる三角メッシュは、全ての三角形が、３点を結ぶ３辺があって、凸な形になっているものを言う
    • 三角メッシュでは、２つの三角形の辺を貼り合わせてメッシュ化する
    • いわゆる三角メッシュでは、辺の貼り合わせにあたり、異なる２つの三角形の辺の貼り合わせをする
    • 一般化した三角メッシュでは、一つの三角形の２辺の貼り合わせも許可する
    • これが違い
    • 一般化三角メッシュによって、新たに登場するのは、「１つの三角形の隣り合う２辺を貼り合わせてできる形」である
    • それは、１頂点から出て、その頂点に戻るループと、そのループの内部に１個の頂点とがあり、ループの始点・終点頂点とループ内部頂点とを結んだ形である。自己貼り合わせ三角形とでも呼ぶ形である
    • ある頂点がループをもち、その内部に１頂点がある状態は、その２頂点に辺を引くと、自己張り合わせ三角形ができる。この自己貼り合わせ三角形を作りうる状態を once-punctured monogonと呼ぶ。monogonとは、１角形（頂点数が１で辺数が１の多角形）のことで、その内部にある頂点を「針刺し穴 puncture」と読んでいる
  • Tagged arc
    • once-punctured monogonを切り取るループは、三角化に当たって、特別な扱いをする必要が出てくる
    • このonce-punctured monogonを切り取るループを、ループの始点・終点の頂点から、内部頂点への辺(arc)に対応づけて置き換えることにする
    • こうすることで、一般化三角メッシュで、自己貼り合わせ三角形を含むメッシュであっても、「ループ」を持っていないとみなすことが可能になる
    • しかしながら、このループを普通の辺に置き換えたことによって、この２頂点間には、二つの辺を考慮する必要が生じる
    • 一つはもともとの普通の辺、もう一つは、once-punctured monogonを切り取るループを意味する「見かけ上の辺」
    • 異なる２つは、区別できた方が良いので、ループに対応する方を、tagged arcとする。図示する時には、それとわかる印をつける
    • なお、このonce-punctured monogonを切り取るループを表すtagged arcが大事だが、「そもそもtagged arcと言うものを導入するなら、それの一般化した定義をしておくのもよかろう」と言うことで、tagged arcとは、と言う定義が別途、存在することにも注意
    • そのようなtagged arcの例として、２つのcusp型点を結ぶarcには両端のtag具合により４通りができる([1210.5569] Cluster algebras and triangulated surfaces. Part II: Lambda lengthsのFigure 7を参照)
  • Tagged arc 導入の意義
    • 三角化を考える時に、二つのグラフを用いる
    • 一つは、取りうるあらゆる辺(arc)を頂点としたグラフでArc complexと呼ばれるもの。これは、ある一揃いのarc の部分集合があった時に、ある三角メッシュが出来上がるような時、そのarcの部分集合がクリークになっているようなグラフ
    • もう一つは、arc complexの双対になるもので、Exchange complexと呼ばれるもの。これは、ある三角メッシュがあった時に、そのうちのただ１つのarcを別の特定のarcに入れ替えることで新たな三角メッシュができることを利用して、三角メッシュ同士の移り変わり関係を表したグラフ
    • 今、arcを普通のarcにして、once-punctured monogonを切り取るarcを使ってarc complexを作り、その双対としてのexchange complexを作ると、ちょっと綺麗な関係にならないことが知られている
    • once-punctured monogonを切り取るarcをtagged arcとして、それぞれのcomplexを作ると、対称性の高いグラフ(例えば、exchange complexなら、正則グラフ(全ての頂点の次数が等しいグラフ))になったりする
    • また、この対称性が高いcomplexにできることが、団代数・団変数として取り扱う時に有用であることも、この記事を書いている目的と関係が深いので、あえて触れておく
    • tagged arcsの交換ルールを含め、tagged arcについて図を用いた説明を貼っておく

f:id:ryamada:20200709053458j:plainf:id:ryamada:20200709053512j:plainf:id:ryamada:20200709053525j:plain

  • 三角化と曲面トポロジー
    • 三角化のパターンは、前項で書いたようにtagged arc、自己貼り合わせ三角形を許せば、団代数・団変数と繋がる「良い」形式にできる
    • Teichmuller spaceが由来する曲面トポロジー的には、もう少し複雑になる
    • Teichmuller spaceは定負曲率閉曲面に対して定まったから、閉曲面の三角化パターンも定負曲率閉曲面化したい
    • そのために、閉曲面上の点(三角形)の頂点をそのまま、ただの閉曲面上の点として見ていたのでは、負曲率な曲面にならない
    • 二つの方法がある
      • 一つは、点を、ちゅどーんと無限遠に飛ばし、周囲の面を裾野のように引っ張り上げること
      • もう一つは、点を、小さな穴として、その穴上の点に向かって、無限に穴の周囲をぐるぐる周回して到達するものとすること。これにより、辺は無限長になり、そこに現れる計量・曲率を定負値とすることができる
    • 今、点を裾野をもつ山に飛ばす方法をcuspにする、と言い、小さな穴をぐるぐる巻きにする方法をboundaryにすると言う
    • boundaryにした場合、arcのぐるぐる巻きには時計回りと反時計回りとの２通りがあり、それも区別するのが、定負曲率曲面のトポロジー分類風
    • したがって、曲面上に点の数がN個あるときは、cuspにする個数kと、boundaryにする個数N-kとの場合分けがあり、boundaryにする方には2^{N-k}の場合分けが発生する
    • つまり\sum_{i=0}^N \begin{pmatrix} N \\ i \end{pmatrix} 2^{N-i}の場合分けがある
    • Teichmuller spaceでは、これらを全て区別する(こともある)
    • この\sum_{i=0}^N \begin{pmatrix} N \\ i \end{pmatrix} 2^{N-i}は、多次元多面体構造をとり、その全ての単体要素が、個々の場合分けに対応する。例えば、N=3の場合には、正八面体になる。N=3なので３次元空間の多面体担っている。全てがboundaryの場合は、2^3=8通りあり、それが、８つの面に対応する。２つがboundaryで1つがcuspの場合は、boundaryの取り方が３通りで、それの巻き方の場合分けが４通りあることから、全部で12通りある。これは、正八面体の辺の数に相当する。boundaryが１個の場合は、３通りにつき、巻きの向きの２通りで、全部で６通り。これが正八面体の６頂点。最後に、全部がcuspの場合はただ一通りで、これを正八面体の重心〜原点に対応づける。例えば、ある面は３点がboundaryの場合である向きのぐるぐるだが、それにも色々な場合があることが、「面」の至る所が、曲面の様子に対応することからもわかる。そして、この３次元空間上の座標がTeichmuller spaceの座標となっており、それは、genusありの閉曲面に見つけた測地線的半ズボン切断閉曲線の長さから得られる座標になっている。参考：

Shift coordinates, stretch lines and polyhedral structures for Teichmüller space | SpringerLinkのFigure 11

    • 他方、三角化のみに興味があるときは、この場合分けは、結局のところ同じ三角化なので、同一視したくなることもある
  • Arc同士の相互関係と団変数
    • Arcには団変数が付随する
    • 団変数は、ある三角化をシードとした時に、その辺の数の団変数セットを用いて、シードに含まれない全ての団変数が有理式で表される。実際には、分母が単項であるローラン多項式になる
    • あるarcをあるシード団変数セットのローラン多項式で表した時、その分母の単項に現れる、あるシード変数の次数は、曲面上で、２つのarcを素直に引いた時の交叉数になると言う性質がある
    • ある三角化では全ての辺が交叉しないので、分母は１である（全ての辺の団変数は、相互に独立）
    • 三角化の変異をしていくと、だんだん、分母の次数が上がってくるが、それは、三角化の違いの程度をある意味で表していると言える
    • ちなみに、tagged arcで考える時、この「交叉数」は少しルールを入れる必要があることに注意。ただし、意味合いとしては、arc同士の関係が団変数の分母の次数によって表現されると言うことは、団代数・団変数と三角化の幾何とを結ぶ情報となる

Teichmuller space 事始め

トポロジー Teichmuller space パンツ
  • Teichmuller space

Teichmüller space - Wikipedia
と言うのものがある

  • 曲面が構造を持っている時に、ある一定の特徴を共有する曲面の集合の要素を、その位相的な同値性を考慮した上で、同値とされた亜集合ごとに座標を与えて出来上がる多様体(manifoldではなくてorbifold)のこと
    • 「ある一定の特徴を共有する曲面の集合」と言うのは、例えば、genus 穴の数が g = 5であるような閉曲面、と言うようなもの
  • 定義としてはこんな感じで単純なので、対象を変えると、どうやって位相的な同値性を決めるか、とか、座標の値をどのように定めるか、とか、具体的な問題が変わるので、話がこんがらがってくる
  • このブログでの目標は、S2同相閉曲面上の三角化のTeichmuller spaceに興味があるので、目標をそこに置く
  • 残念なことに、そこをいきなり理解しようとすると、Teichmuller spaceの基礎事項を知っていることを前提とした資料に直面し、にっちもさっちも行かなくなるようなので、その手前からスタートする
  • 事始め、としては、genus, g > 1 の閉曲面に、Fenchel–Nielsen coordinatesと言う座標系の点を対応づける話を理解することとする
  • 資料はこちら
  • A pair of pants
    • 第一に、このa pair of pants と言う単語を理解しよう
    • リンク先資料の、一番最初の図がそれである

f:id:ryamada:20200705104627p:plain

    • いわゆる、半ズボンの形をした曲面。穴のない球面に３つの穴（２本の脚が出る穴と、１つの胴体が出る穴の３つ）があいた曲面のことである。二つの半ズボンをつなぎ合わせて、"A pair of two pairs of pants"などと書かれることもあって、混乱するので、「半ズボン」と呼ぶことにする。「二つの半ズボンの胴体穴同士をつなぎ合わせる」と表現すれば、４本の脚が出る胴体なしの生物用の服のことであることがわかりやすいはず
    • 第二に理解することは、g > 1 の閉曲面は、相互に交叉しない単純な（自己交叉しない）閉曲線によって、半ズボンに分けることができることである。リンク先資料の二番目の図がそれを表している。穴の数　g = 3 に対して、４つの半ズボンに分けられている

f:id:ryamada:20200705104645p:plain

    • 3g-3 本の閉曲線によって、2g - 2 個の半ズボンに分けられることになっている
    • 第三の理解ポイントは、ある特定のgの値を定めても、半ズボンの分け方は一通りではないこと
    • 例えばg=2の時、二つの穴の間に、穴をくぐらない閉曲線をとって、２分する。分離したそれぞれは、穴が一つしか開いていないので、その穴を胴体穴とみなし、その上で、できた２パーツの脚の出る穴を作る方法がある。他方、二つの穴を潜る閉曲線で切り開く。そうすると、曲面はまだひとかたまりのままで、胴体穴が２つ開いており、二つの半ズボンは脚の出る穴が、もう片方の半ズボンの脚の出る穴と縫い合わさっている状態なので、それを切り離して、二つの半ズボンを得ることができる

f:id:ryamada:20200705105311p:plain

    • 第四のポイントは、半ズボン曲面を双曲面とみなすことと、内角が全て直角な六角形が大事であること
    • 双曲面は、ガウス曲率が負(-1に統一するらしい)で、その上に多角形を描くと、その内角の和は、ユークリッド平面が要請する決まりを満たさなくて良い。具体的には、３つの穴（胴体穴、脚の出る二つの穴）のそれぞれの間に、測地線を引いて、穴の周囲曲線に垂直に刺入するようにできる。３本の測地線のそれぞれの両端が、穴の周囲曲線と直角に交わるから、内角が全て直角である六角形ができる。それを示したのがリンク先資料の四番目の図である。また、このように３本の測地線で六角形を作ると、半ズボンは二つの面に別れるが、２つの面はそれぞれ、六角形であって、内角は全て直角である

f:id:ryamada:20200705105412p:plain

    • 第五ポイントが最後のポイント。座標を入れる。Fenchel-Nielsen
    • 今、g > 1 閉曲面の全体を考えるが、ある程度の制約を入れる。全ての分割半ズボンが双曲面であり、分割閉曲線部分でも滑らかに連続しているような閉曲面に限定する
    • この時、閉曲線の取り方を決めると、その閉曲線は色々な取り方ができるが、最短線・測地線になるように限定する。こうすると、元の穴あき閉曲面の分割のやり方に応じて、3g-3個の閉曲線の「長さ」が確定する。この3g - 3 個の実数値が、Fenchel-Nielsen 座標の値の半分に相当する
    • 2g-2個の半ズボンから元の穴数 g の閉曲面を復元するには、どの半ズボンのどの穴同士を縫い合わせるかの情報がないと困る。それがあってこそ、元の閉曲面の情報を持っていると言える
    • リンク先資料の最後の図を見てみる。赤い閉曲線は、半ズボンに分割するための閉曲線

f:id:ryamada:20200705105508p:plain

    • それとは別に青い閉曲線が描かれている。よく見ると、青い閉曲線の数は、赤い閉曲線の数と同じである
    • 青い閉曲線は、赤い閉曲線から、２つの連結した半ズボンにそれぞれ向かう。一つの半ズボンに着目すると、出発した赤い閉曲線の向かい側にある「股」を通って、赤い閉曲線に戻ってくる。そしてもう片方の半ズボンに入り、同様に、赤い閉曲線の向かい側にある「股」を通って、元の点に戻る。このような曲線のうち、測地線になっているものを使うことにする。赤線と青線とは直角に交わる。このような測地線の長さは、オリジナルの閉曲面に依存する値である。この値は、赤い閉曲線の数だけあるので、3g - 3個の値が得られる。
    • 結局、赤い閉曲線と青い閉曲線（いずれも測地線）の長さとして、合わせて6g- 6個の値が得られる
    • この6g - 6個の値が、「閉曲面」のTeichmuller spaceにおけるFrechel-Nielsen座標と呼ばれるものである
    • 補足。最後にTwistと言う概念を書いておく。リンク先資料の下から三番目の図では、青い曲線が曲面上でぐるぐる巻きをしている。こう言うぐるぐる巻きは青曲線の長さを無駄に長くしてしまい、座標として一意性を確保できないことから、半ズボンの連結では、曲面をtwist（実際には、曲面上の「パスを無駄にぐるぐる回り」）しないで連結することを基本とする、と言う考え方がある

f:id:ryamada:20200705105542p:plain

  • ここまでのまとめ
    • Teichmuller spaceは
      • (1) 曲面の特徴を実数値のセットとして表してくれる。したがってある一つの曲面を多次元実数空間の点に対応づける
      • (2) 曲面を少しずつ変えると、実数値ベクトルも少しずつ変わることも知られている。その変化は微分可能であり、結局、曲面集合が多次元実数空間に埋め込まれた多様体とみなせる。これがTeichmuller space。また、実数値ベクトルの要素の積も、曲面の変化に応じて微分可能な関数となっており、そのことが記述されることもある
      • (3) なお、対象とする曲面はガウス曲率が至る所で -1 であるあるようなものが対象となる。つまり双曲面が対象となる（なんだ、つまんないじゃん、という感じがするが理由もある。一見、双曲面出ない対象を双曲面扱いすれば、Teichmuller spaceでの議論ができる、と思い直す方が生産的)
      • (4) 負の定曲率曲面では、連続して移り合える単純な閉路を同一視した時、ただ一つの最短なそれ(geodesic)なもので代表させられるとされる("Shear coordinates on the Teichmuller space of real hyperbolic surfaces with holes"のProposition 2.2)。これにより、曲面の位相的特徴を測地閉路長のセットに対応づけできることになる。また、いわゆるgenus 穴のある閉曲面は負の定曲率曲面でできた半ズボンの連結と位相的に表せることから、genus穴を持つ閉曲面の定量的位相特徴量の取り出しに使える
  • 三角メッシュのTeichmuller spaceの議論のための前置き
    • 全内角が直角な六角形の交互３辺を無限遠に飛ばして１点とみなすと、全内角が直角な三角形が現れる
    • その貼り合わせを三角メッシュとみなせる
    • この「貼り合わせ」って言うのが「ミソ」で、穴あき閉曲面も半ズボンの貼り合わせ、三角メッシュも辺の貼り合わせ
    • 貼り合わせは「ペアづくり」であって、特殊な置換（この辺りが全正値行列のminorに置換が出てきたことと無縁ではなさそう）
    • 無限遠点が登場するので、その点をcuspとして、超トンガリとみなしたり、小さい円周を無限にぐるぐる巻きにすることで無限遠点になるようにしたりする
    • g = 0なので半ズボンは登場しないが、その切れ端としての六角形は登場する
    • 半ズボン分割のための単純な閉曲線の取り方のパターンを曲面上の構造として、位相分類し、その閉曲線の取り方に依存して決まる測地距離を座標値としたが、三角形メッシュの場合は、閉曲面上の点集合に描く平面グラフ・三角メッシュのエッジ(arc)の取り方のパターンを曲面上の構造として、位相分類する
    • このTeichmuller spaceの座標次元は 6g -6 + 3k (kは曲面上のmark点の数)と言われている。例えばg=0の場合、3k-6がその次元。普通のg=0閉曲面上の三角メッシュでは、頂点数 u+2に対して、三角形数 2u、辺数 3u、であるしたがって、3k - 6 = 3(u+2) - 6 = 3u であり、これはエッジ数にあたる
    • 三角メッシュの場合のTeichmuller座標系はエッジに付与される値を座標とするものとして実現されることがわかる
    • ここから、エッジ団辺数とTeichmuller座標とに関係が生じるっぽい