SAGEでリーマンの写像定理遊びをする

• 単位円板と同相な面があったとき、conformalな写像が存在して、単位円板に滑らかに移せる、しかもしれは一意、というのがリーマンの写像定理
• 存在証明と一意性の証明はされるものの、「みつける」のは面倒くさくて、計算機的にはちまちまと計算するらしい
• 数学アプリのsageにはそれがあって、最近のsageはjupyter notebookでさらさらとじっこうできる。背後ではpythonのベクトル・行列状データ保持などを使っていることもあり、pythonでやっているようなつもりでできる
• sageのインストールはこちら

www.sagemath.org
。こちらでもよい

• さて、立ち上がるようになったら、Riemannの写像定理の実例ページに行ってみよう
• 絵が出るコードがないと、楽しめないので、例えばこちら

projecteuclid.orgに行ってみよう

• いろいろあるけれど、多角形にうまいこと単位円板と対応付けられる座標系を描いてくれそうな図とコードがあるのでやってみる
• インストールしたSAGE-MATHのjupyter版を起動すれば、jupyter notebookが立ち上がるので、あ他らしいノートブックを作る。もちろん、実行カーネルはsage-math

ps = polygon_spline([(-1,-1),(1,-1),(1,1),(-1,1)])
z = lambda t: ps.value(t) # Riemann map for a square
zp = lambda t: ps.derivative(t)
m = Riemann_Map([z],[zp],.3+.3*I)
p = m.plot_colored(plot_points=1000) +m.plot_spiderweb(pts=150)
show(p,axes=false)

• これをrunしてエラーが出なければOK

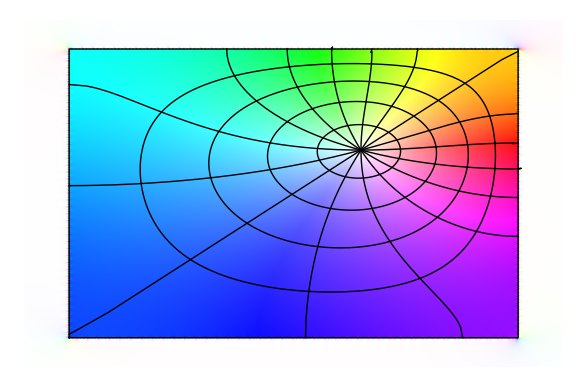
• このコードが何をしているのかが読みとれれば、改変して使えるはず

ps = polygon_spline([(-1,-1),(1,-1),(1,1),(-1,1)])

• 多角形とその(内部)のスプライン曲線をいじる関数っぽい。２次元４点を指定している模様であり、それは、出力図とも符合するから、そう信じてよさそう

z = lambda t: ps.value(t) # Riemann map for a square

• 作った多角形psに何かしら変数tを与えて計算しているっぽい。実際、この変数tはデフォルトで実数値パラメタとして適当な幅等で作るものらしいので、使うことする。zに何かpsの領域に値付けがされたことになる

zp = lambda t: ps.derivative(t)

• こちらも同様に多角形ps内に値を与える処理らしい。derivativeという用語からわかるように微分と関係しているのだろう。滑らかにしたいし、conformalにしたいから、微分は大事なのでしょう

m = Riemann_Map([z],[zp],.3+.3*I)

• ここにRiemann_Map()なる、いかにも「本体」な関数が出ている。ps内部に算出した２種類の値 zとzsとを引数として取り、第三の引数 .3 + .3 * I を取っている。これは複素数。図を見ると、座標系の中心を定めた極座標形式の曲線群が描かれているから、その曲線群の「中心」は大事な役割なはずであることがわかる。確かに、第三引数である複素数を複素平面上の点としたときの位置が、曲線群の「起点」になっているから、起点指定をしているのだろうと想像がつく

p = m.plot_colored(plot_points=1000) +m.plot_spiderweb(pts=150)
show(p,axes=false)

• これは見るからに、プロット。colorに関することと、spiderweb(中心を持った蜘蛛の巣に関することを、点の数で指定しているように読めるから、図の解像度だろうと予想される。色は、複素数の様子を表すためのもの、蜘蛛の巣は、単位円板だったら、射的の的の極座標に相当するもの
• これで準備は終わり
• spiderwebの方だけ、もう少し、パラメタ指定を細かくできるようになっておくと便利そうなので、help(m.plot_spiderwb)などで調べておく
• さあ、本題
• 適当な多角形でやってみよう

ps = polygon_spline([(0,0),(1,0),(3/2,sqrt(3)/2),(1,sqrt(3)),(0,sqrt(3)),(1/2,sqrt(3)/2)]) # 正三角形の貼り合わせ
z = lambda t: ps.value(t) # Riemann map for正三角形の貼り合わせ
zp = lambda t: ps.derivative(t)
m = Riemann_Map([z],[zp],1.0+sqrt(3)/2*I) # 中心を (1.0, sqrt(3/2)として描く
p = m.plot_colored(plot_points=100) +m.plot_spiderweb(spokes=64, circles=8,pts=30) # 極座標の放射線の数と輪の数を追加指定してみた
show(p,axes=false)

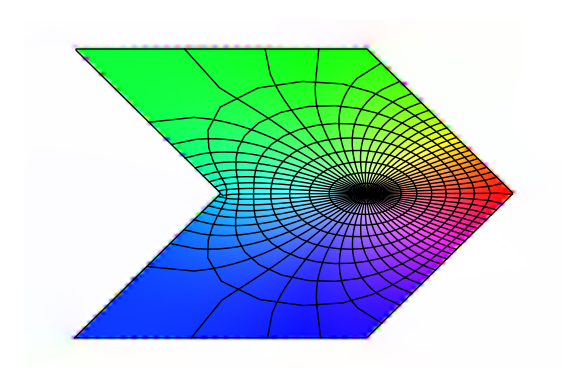
ps = polygon_spline([(0,0),(1,0),(3/2,sqrt(3)/2),(1,sqrt(3)),(0,sqrt(3)),(1/2,sqrt(3)/2)]) # 正三角形の貼り合わせ
z = lambda t: ps.value(t) # Riemann map for正三角形の貼り合わせ
zp = lambda t: ps.derivative(t)
m = Riemann_Map([z],[zp],0.2+0.2*I) # 中心を変えてみた
p = m.plot_colored(plot_points=100) +m.plot_spiderweb(spokes=64, circles=8,pts=150)
show(p,axes=false)

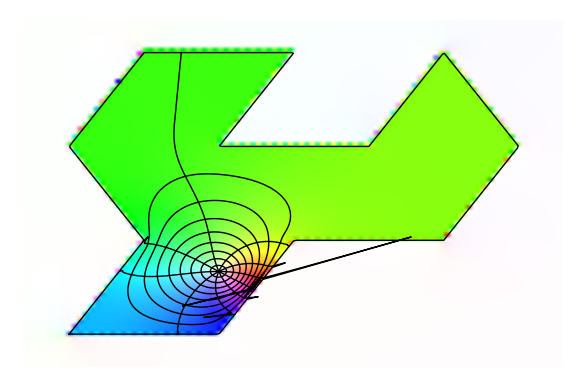
• 中心を変えると、凹になったところがちょっとうまく行っていない感じ。リーマンの写像定理は、凹凸があってもいけるはずなので、この辺りは、今使っている計算関数の仕様が、そのあたりをはしょっているせいなのかなー、と思われる。詳しくは、計算アルゴリズムの説明に当たらないといけないが、遊びだから良しとしよう

• さらに形を複雑にすると、spiderwebに無理が生じることがわかり、関数のアルゴリズムが端折っているせいだという予想がさらに高まる…

ps = polygon_spline([(0,0),(1,0),(3/2,sqrt(3)/2),(5/2,sqrt(3)/2),(3,sqrt(3)),(5/2,3*sqrt(3)/2),(2,sqrt(3)),(1,sqrt(3)),(3/2,3*sqrt(3)/2),(1/2,3*sqrt(3)/2),(0,sqrt(3)),(1/2,sqrt(3)/2)]) # 正三角形の貼り合わせ
z = lambda t: ps.value(t) # Riemann map for正三角形の貼り合わせ
zp = lambda t: ps.derivative(t)
m = Riemann_Map([z],[zp],1.0+sqrt(3)/3*I) # 中心を (1.0, sqrt(3/2)として描く
p = m.plot_colored(plot_points=100) +m.plot_spiderweb(spokes=10, circles=8,pts=150)
show(p,axes=false)