疎四元数行列の実行列版

• 四元数行列は、個々の四元数を４ｘ４行列と見立てて、行・列、ともに４倍にした実行列にしてから、実数計算に持ち込む
• 今、10x10の四元数疎行列に相当するデータを作る
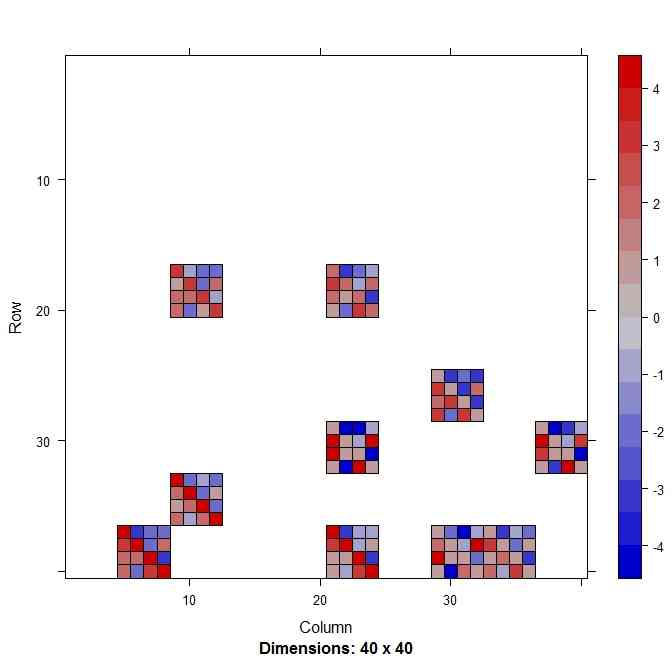
  • 10要素だけが非０として、整数係数ランダム四元数を10個作り、それを実、i,j,k成分ごとに疎ベクトルとして、リストにして、そこから40x40実行列を作って、イメージ表示する。4x4単位で散らばっていることがわかる

# 四元数対応実行列作成

my.qMtorM <- function(Es){
	n <- sqrt(length(Es[[1]]))
	N <- (n*4)^2
	init.id <- c(1:4,(1:4)+n*4,(1:4)+n*4*2,(1:4)+n*4*3)
	spacing.id <- c(outer((0:(n-1)*4),n*4*4*(0:(n-1)),"+"))
	ret <- sparseVector(c(0),i=c(1),N)
	a <- c(1,2,3,4,2,1,4,3,3,4,1,2,4,3,2,1)
	b <- c(1,1,1,1,-1,1,1,-1,-1,-1,1,1,-1,1,-1,1)
	for(j in 1:length(a)){
		tmp.v <- sparseVector(b[j] * Es[[a[j]]]@x,i=init.id[j]+spacing.id[Es[[a[j]]]@i],length=N)
		ret <- ret + tmp.v
	}
	Matrix(ret,n*4,n*4)
}

N <- 10
n <- N^2
p <- 80
s <- sample(1:n,p)
h <- rquat(p)
tmp.Es.v <- list(sparseVector(Re(h),s,n),sparseVector(i(h),s,n),sparseVector(j(h),s,n),sparseVector(k(h),s,n))

tmp.Es.real <- my.qMtorM(tmp.Es.v)

image(tmp.Es.real)

• 四元数ベクトルを長さが４倍の実ベクトルに換えるのは簡単

my.qVtorV <- function(v){
	c(as.matrix(v))
}
tmp.v <- rquat(4)
tmp.v
my.qVtorV(tmp.v)

> tmp.v
   [1] [2] [3] [4]
Re   1   3   1   3
i    4   1   4   1
j    3   3   2   4
k    3   2   2   1
> my.qVtorV(tmp.v)
 [1] 1 4 3 3 3 1 3 2 1 4 2 2 3 1 4 1

• Mx=bという四元数行列・四元数ベクトルの線形代数方程式解を解くのも簡単

# 四元数行列(ベクトルリスト形式)Mと
# 四元数ベクトルbとの
# Mx = b の解

my.linear.solver <- function(Es,b){
	b.re <- my.qVtorV(b)
	E.re <- my.qMtorM(Es)
	solve(E.re,b.re)
}
N <- 10
n <- N^2
p <- 80
s <- sample(1:n,p)
h <- rquat(p)
tmp.Es.v <- list(sparseVector(Re(h),s,n),sparseVector(i(h),s,n),sparseVector(j(h),s,n),sparseVector(k(h),s,n))
tmp.v <- rquat(10)

my.linear.solver(tmp.Es.v,tmp.v)