- こちらでやっている、三角メッシュの変形をなぞって、そのやり方を確認する
- 変形というのは以下のようなこと(上記リンク先より)
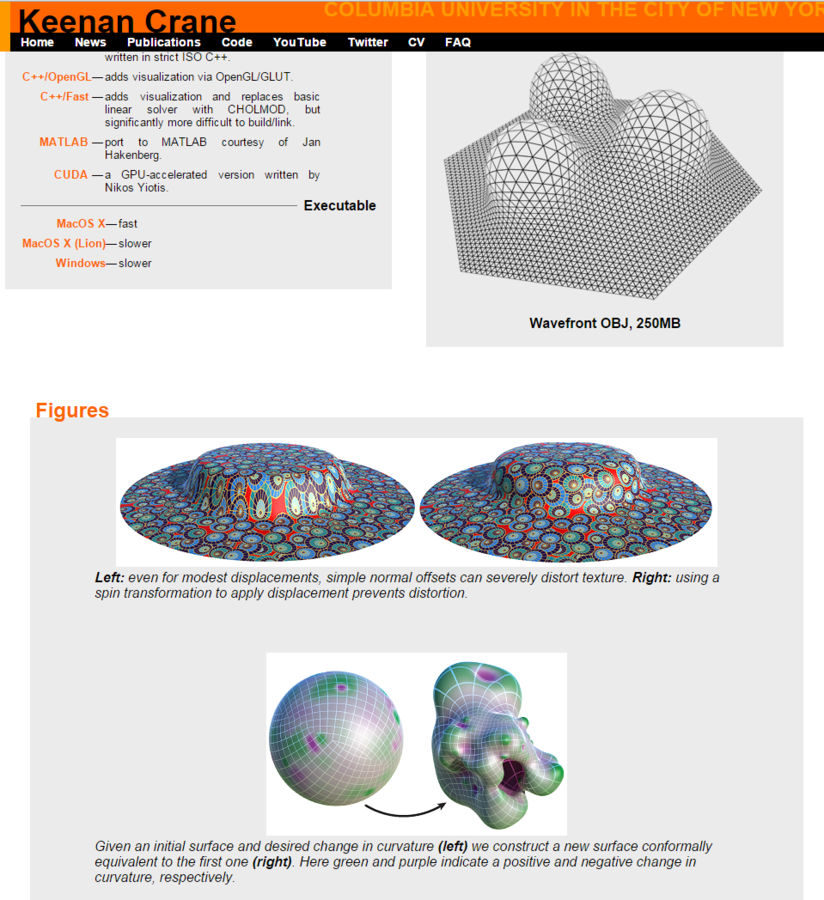
- 資料はこちらと、こちら、そしてC++ソース(こちら)
- 入出力
- 入力
- 出力
- (3) 入力(1),(2)から算出した「新たに曲げた曲面」の情報
- (1) 曲面の情報
- (2) 曲面の曲げ方の情報
- 三角形を二次元平面に対応付ける。三角形の三頂点を曲面をつくる三角形メッシュの頂点に対応付けたが、同様に、三角形の三頂点を二次元平面上の点に対応付ける
- そのうえで、二次元平面座標に曲げ情報をスカラー値で与える
- オブジェクト化
- vertices,newVertices
- 頂点の３次元座標(x,y,z)を四元数の虚部に持たせて、長さn.v(頂点数)の四元数ベクトルとして作る
- verticesは元の３次元座標、newVerticesは変形後のそれ
- uv
- 二次元平面上の点の３次元座標(x,y,0)を３次元実ベクトルとして、そのような点を多数登録する
- faces
- 三角形面は、３頂点の組として登録する。ただし、verticesのIDの３つとuvのIDの３つとを持たせる
- rho
- (2)曲面の曲げ方の情報から、各faceについて「曲げの程度」を実スカラーとして与えるが、それを納めるベクトル
- 曲面の曲げ方情報を二次元平面グレースケール画像で与える場合には、uv座標からrhoの値を線形保管で算出する、というような方法をとる
- lambda
- 入力情報から、verticesのそれぞれに対応する四元数を推定するが、それを格納する四元数ベクトル
- これは、各vertexにおける、「回転」を表す四元数
- ３次元幾何を四元数で扱うとき、
という計算(四元数とその共役四元数ではさんだ積)によって座標の回転変換ができるのだが、そのような
をすべてのverticesに滑らかに推定する
- どうして曲面上に滑らかに変化する回転を定義することがよいのか、と言えば、それは、「共形変換は局所において接平面に関する回転である」とわかっているから
- 実際、このの推定にあたっては、逆べき乗法を使うと速いので、そのようにすることになる
- omega
- verticesのそれぞれに自身とその周辺verticesのlambda値(四元数)によって四元数を算出するが、その値のベクトル
- 点の数ｘ点の数の四元数行列 E
- faceは面積とrho値を持つが、それによって、faceを構成する辺ごとに頂点vertex_i,vertex_jに対応するセルの値を計算する
なる関係にある。ここで、
は何でもよいので、すべての固有値・固有ベクトルを求める代わりに、最小固有値に対応する固有ベクトルを算出することで、計算を軽くする
- 点の数ｘ点の数の実行列 L
- 各vertexには、自身を取り巻く三角形がある。その三角形の角度の情報を用いて定まる行列
を解くことで変形後の頂点座標newVerticesが決まる。ただし、Lは点の数ｘ点の数の実行列だが、それを虚部0の四元数と見立てて、四元数に対応する、(点の数ｘ４）ｘ(点の数ｘ４）の行列とし、newVerticesとomegaは点の数ｘ４の実行列として解く
- さて、Rで書いてみよう…と思ったけれど、ここまでわかってしまえば、C++をそのままRに連結するなり、Rのvrmlgenパッケージを使って、ブラウザにVRML-plugin(これとか)を入れて、表示させてもよいだろう。
library(vrmlgen)
mesh3d(obj_infile = "bumps_deformed.obj", filename = "bumps_deformed.wrl", cols = "lightblue", showaxis = FALSE, htmlout = "bumps_deformed.html")
browseURL(paste("file://", file.path(getwd(), "bumps_deformed.html"), sep = ""))
- Rで書くなら
- まず、Wavefront OBJフォーマットを読み込もう。vrmlgenパッケージの読み込みファイルは、法線ベクトル、テクスチャ情報に対応していないので、三角化されていることを前提に、書き換えて使う("sphere_deformed.obj"はこちらのDataから。
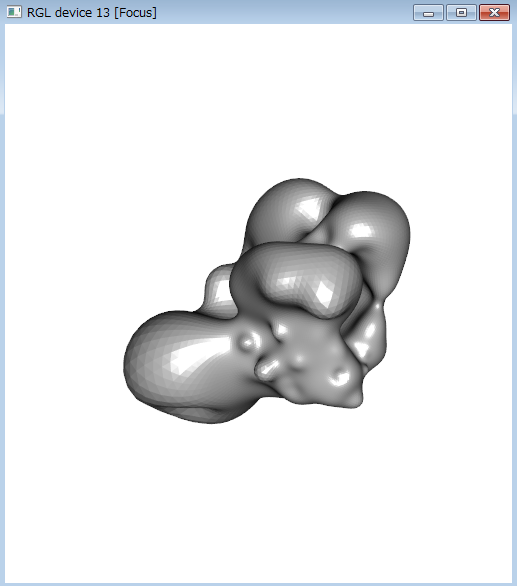
my.readOBJ <-
function (con, ...)
{
lines <- readLines(con)
instrs <- sub(" .*", "", lines)
vertices <- read.table(textConnection(lines[instrs == "v"]),
col.names = c("instr", "x", "y", "z"), colClasses = c(instr = "character",
x = "numeric", y = "numeric", z = "numeric"))
vertices <- with(vertices, rbind(x, y, z))
normals <- c()
normals <- read.table(textConnection(lines[instrs == "vn"]),
col.names = c("instr", "x", "y", "z"), colClasses = c(instr = "character",
x = "numeric", y = "numeric", z = "numeric"))
normals <- with(normals, rbind(x, y, z))
textures <- c()
textures <- read.table(textConnection(lines[instrs == "vt"]),
col.names = c("instr", "x", "y"), colClasses = c(instr = "character",
x = "numeric", y = "numeric"))
textures <- with(textures, rbind(x, y))
tfaces <- grepl("^f\\W+\\w+\\W+\\w+\\W+\\w+$", lines)
triangles <- read.table(textConnection(lines[instrs == "f"]), col.names = c("instr",
"v1", "v2", "v3"), colClasses = "character")
triangles <- with(triangles, rbind(v1, v2, v3))
triangles1 <- triangles2 <- triangles3 <- matrix(0,3,length(triangles[1,]))
for(i in 1:length(triangles[1,])){
for(j in 1:3){
tmp <- unlist(strsplit(triangles[j,i],"/"))
triangles1[j,i] <- as.numeric(tmp[1])
triangles2[j,i] <- as.numeric(tmp[2])
triangles3[j,i] <- as.numeric(tmp[3])
}
}
ret <- list(vertices=vertices,normals=normals,textures=textures,triangles1=triangles1,triangles2=triangles2,triangles3=triangles3)
return(ret)
}
con <- "sphere_deformed.obj"
obj.data <- my.readOBJ(con)
m <- tmesh3d(obj.data$vertices,obj.data$triangles1,homogeneous=FALSE)
shade3d(m)
- これを、上述のverticesとuv,facesに入れ込もう
library(onion)
vertices <- obj.data$vertices[,1] * Hi + obj.data$vertices[,2] * Hj + obj.data$vertices[,3] * Hk
uv <- obj.data$textures
faces.v <- obj.data$triangles1
faces.uv <- obj.data$triangles2
- rhoは、参照サイトでは２次元グレースケール画像データから作っているが、ここでは、obj.data$texturesの範囲に適当な[0,1]の関数を与えることにする
- 三角形ごとのrhoの値は、３頂点の値の平均として、その値が[-5,5]の範囲になるようにするとよいらしい
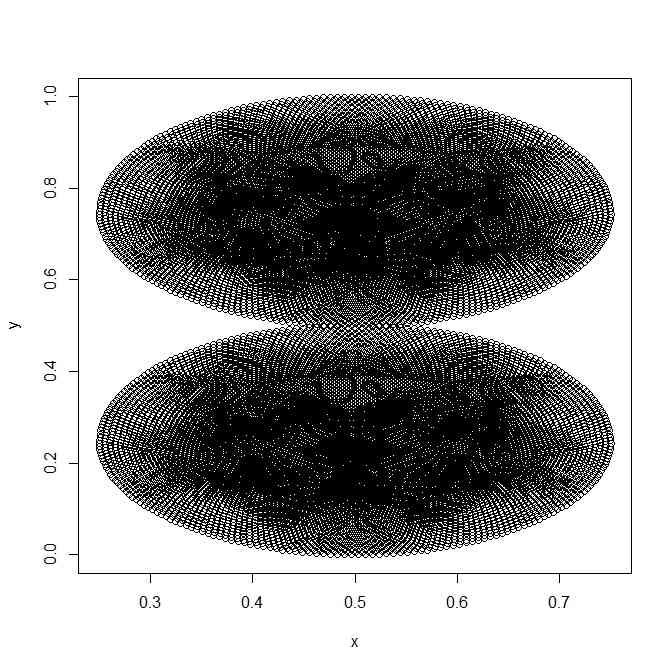
plot(obj.data$textures)
- それに際して、参照サイトが与えている「曲り具合情報」の画像は、以下のように、２つの円の周辺で滑らかに、もう片方の円に移行するようになっている(そうでないと、曲り具合情報が曲面全体で滑らかになっていない)
- 例えば、球面上の滑らかな関数を作り、それを平板に押しつぶして２円に分けてみる
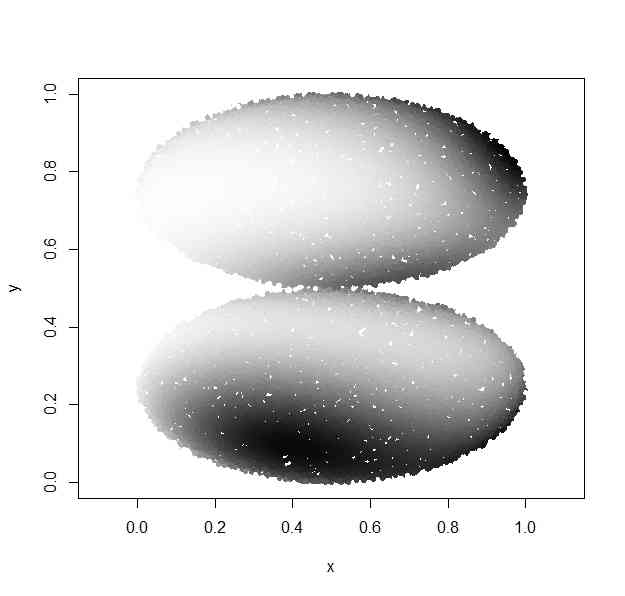
my.rho <- function(x,y,vs,Vs){
X <- x
Y <- y
if(Y < 0.5){
Y <- y*2
}else{
Y <- 2*(y-0.5)
}
X <- (X-0.5)*2
Y <- (Y-0.5)*2
if(X^2+Y^2>1){
return(0)
}
if(y < 0.5){
Y <- -Y
Z <- sqrt(1-(X^2+Y^2))
}else{
Z <- -sqrt(1-(X^2+Y^2))
}
xyz <- c(X,Y,Z)
tmp <- (t(vs) %*% xyz)
for(i in 1:length(tmp)){
if(tmp[i] > 1) tmp[i] <- 1
if(tmp[i] < -1) tmp[i] <- -1
}
tmp <- acos(tmp)
ret <- sum(exp(-Vs*tmp^2))
ret
}
x <- runif(30000)
y <- runif(30000)
np <- 4
vs <- matrix(rnorm(np*3),ncol=3)
vs <- vs/sqrt(apply(vs^2,1,sum))
vs <- t(vs)
Vs <- runif(np)*5
rho <- rep(0,length(x))
for(i in 1:length(rho)){
rho[i] <- my.rho(x[i],y[i],vs,Vs)
}
rho[which(rho==0)] <- min(rho[rho!=0])-0.01
rho.st <- (max(rho)-rho)/(max(rho)-min(rho))
plot(x,y,col=gray(rho.st),pch=20,asp=TRUE)
- rhoを計算できる関数ができたので、uvから作っておく
rho <- rep(0,length(faces.uv[1,]))
for(i in 1:length(rho)){
threes <- faces.uv[,i]
tmp <- rep(0,3)
for(j in 1:3){
tmp[j] <- my.rho(obj.data$textures[1,threes[j]],obj.data$textures[2,threes[j]],vs,Vs)
}
rho[i] <- mean(tmp)
}
- 行列Eの作成
- 行列Eは頂点数ｘ頂点数の四元数行列
- 第i頂点と第j頂点に関するEの要素E[i,j]は、辺i-jを持つ三角形についてある値を加算したものとなる
- 疎行列を扱いたいのと、その疎行列要素へのアクセスが辺の属する三角形の数だけ発生する、などの理由から少し工夫がいる(こちらを参照)
make.E <- function(vertices,faces.v,rho){
edge1 <- vertices[faces.v[2,]]-vertices[faces.v[1,]]
edge2 <- vertices[faces.v[3,]]-vertices[faces.v[1,]]
tmp <- edge1 * edge2
A <- abs(i(tmp)+j(tmp)+k(tmp))/2
coef.a <- -1/(4*A)
coef.b <- rho/6
coef.c <- A*rho^2/9
E.re <- E.i <- E.j <- E.k <- sparseVector(c(0),i=c(1),length=length(vertices)^2)
e.q <- list()
e.q[[1]] <- vertices[faces.v[2,]]-vertices[faces.v[3,]]
e.q[[2]] <- vertices[faces.v[3,]]-vertices[faces.v[1,]]
e.q[[3]] <- vertices[faces.v[1,]]-vertices[faces.v[2,]]
for(i in 1:3){
for(j in 1:3){
tmp <- coef.a * e.q[[i]] * e.q[[j]]+ coef.b * (e.q[[j]] -e.q[[i]] ) + coef.c
addr <- faces.v[i,] + (length(vertices)*(faces.v[j,]-1))
tmp.v <- t(as.matrix(tmp))
tmp.out <- my.vector.access(tmp.v,addr)
E.re <- E.re + sparseVector(tmp.out[[2]][,1],tmp.out[[1]],length(vertices)^2)
E.i <- E.re + sparseVector(tmp.out[[2]][,2],tmp.out[[1]],length(vertices)^2)
E.j <- E.re + sparseVector(tmp.out[[2]][,3],tmp.out[[1]],length(vertices)^2)
E.k <- E.re + sparseVector(tmp.out[[2]][,4],tmp.out[[1]],length(vertices)^2)
}
}
return(list(E.re=Matrix(E.re,length(vertices),length(vertices)),E.i=Matrix(E.i,length(vertices),length(vertices)),E.j=Matrix(E.j,length(vertices),length(vertices)),E.k=Matrix(E.k,length(vertices),length(vertices))))
}
make.E.v <- function(vertices,faces.v,rho){
edge1 <- vertices[faces.v[2,]]-vertices[faces.v[1,]]
edge2 <- vertices[faces.v[3,]]-vertices[faces.v[1,]]
tmp <- edge1 * edge2
A <- abs(i(tmp)+j(tmp)+k(tmp))/2
coef.a <- -1/(4*A)
coef.b <- rho/6
coef.c <- A*rho^2/9
E.re <- E.i <- E.j <- E.k <- sparseVector(c(0),i=c(1),length=length(vertices)^2)
e.q <- list()
e.q[[1]] <- vertices[faces.v[2,]]-vertices[faces.v[3,]]
e.q[[2]] <- vertices[faces.v[3,]]-vertices[faces.v[1,]]
e.q[[3]] <- vertices[faces.v[1,]]-vertices[faces.v[2,]]
for(i in 1:3){
for(j in 1:3){
tmp <- coef.a * e.q[[i]] * e.q[[j]]+ coef.b * (e.q[[j]] -e.q[[i]] ) + coef.c
addr <- faces.v[i,] + (length(vertices)*(faces.v[j,]-1))
tmp.v <- t(as.matrix(tmp))
tmp.out <- my.vector.access(tmp.v,addr)
E.re <- E.re + sparseVector(tmp.out[[2]][,1],tmp.out[[1]],length(vertices)^2)
E.i <- E.re + sparseVector(tmp.out[[2]][,2],tmp.out[[1]],length(vertices)^2)
E.j <- E.re + sparseVector(tmp.out[[2]][,3],tmp.out[[1]],length(vertices)^2)
E.k <- E.re + sparseVector(tmp.out[[2]][,4],tmp.out[[1]],length(vertices)^2)
}
}
return(list(E.re=E.re,E.i=E.i,E.j=E.j,E.k=E.k))
}
Es <- make.E(vertices,faces.v,rho)
Es.v <- make.E.v(vertices,faces.v,rho)
- 四元数行列の扱いについて、いくつかのユーティリティ関数をこちらに書いたが、それを使って、
のを取り出したい。逆べき乗法を使えばよいということなので、適当なbを初期ベクトルとしたうえで、
を解くことを繰り返せばよい。おおまかな近似解でよいなら、１回、解くだけでよい
- やってみれば、まあ、時間がかからないわけではないが、待ちくたびれる、というほどではなく、計算は終わる。MatrixパッケージがSuiteSparseを実装してくれているから…これで、C++版のSuiteSparseが頑固にコンパイルエラーを吐いている難所は越えた、ということだろうか
my.qMtorM <- function(Es){
n <- sqrt(length(Es[[1]]))
N <- (n*4)^2
init.id <- c(1:4,(1:4)+n*4,(1:4)+n*4*2,(1:4)+n*4*3)
spacing.id <- c(outer((0:(n-1)*4),n*4*4*(0:(n-1)),"+"))
ret <- sparseVector(c(0),i=c(1),N)
a <- c(1,2,3,4,2,1,4,3,3,4,1,2,4,3,2,1)
b <- c(1,1,1,1,-1,1,1,-1,-1,-1,1,1,-1,1,-1,1)
for(j in 1:length(a)){
tmp.v <- sparseVector(b[j] * Es[[a[j]]]@x,i=init.id[j]+spacing.id[Es[[a[j]]]@i],length=N)
ret <- ret + tmp.v
}
Matrix(ret,n*4,n*4)
}
n <- 100
p <- 10
s <- sample(1:n,p)
h <- rquat(p)
tmp.Es.v <- list(sparseVector(Re(h),s,n),sparseVector(i(h),s,n),sparseVector(j(h),s,n),sparseVector(k(h),s,n))
N <- 10
n <- N^2
p <- 80
s <- sample(1:n,p)
h <- rquat(p)
tmp.Es.v <- list(sparseVector(Re(h),s,n),sparseVector(i(h),s,n),sparseVector(j(h),s,n),sparseVector(k(h),s,n))
tmp.Es.real <- my.qMtorM(tmp.Es.v)
image(tmp.Es.real)
my.qVtorV <- function(v){
c(as.matrix(v))
}
tmp.v <- rquat(10)
tmp.v
my.qVtorV(tmp.v)
my.linear.solver <- function(Es,b){
b.re <- my.qVtorV(b)
E.re <- my.qMtorM(Es)
solve(E.re,b.re)
}
N <- 10
n <- N^2
p <- 80
s <- sample(1:n,p)
h <- rquat(p)
tmp.Es.v <- list(sparseVector(Re(h),s,n),sparseVector(i(h),s,n),sparseVector(j(h),s,n),sparseVector(k(h),s,n))
tmp.v <- rquat(10)
my.linear.solver(tmp.Es.v,tmp.v)
b <- rep(1+1*Hi+1*Hj+1*Hk,nrow(Es[[1]]))
tmp.out <- my.linear.solver(Es.v,b)
plot(tmp.out)
- 逆冪乗法を使うことにすれば、四元数行列（と四元数ベクトル）を実数版にした上で、逆冪乗法を実施
- これで、各点のが出る。は局所スカラーであって、曲率を反映した値。これが線形二乗法で曲面全体に滑らかになるように計算してある。ここでは二つの近似がある。一つは、線形二乗法という近似、もう一つは、固有ベクトルの逆冪乗法的な近似。さらには、固有ベクトルは他にもたくさんあるけれど、「とりあえずの一つ（固有値の絶対値が一番小さいものに対応する固有ベクトル）」ということも、念のため、思い出しておく
my.inv.pow <- function(A,n.iter=3,b=rep(1,ncol(A)),log=FALSE){
x <- b
if(log){
x.log <- matrix(0,n.iter+1,ncol(A))
x.log[1,] <- x
}
A. <- solve(A)
for(i in 1:n.iter){
x <- A. %*% x
x <- x/sqrt(sum(x^2))
if(log){
x.log[i+1,] <- x
}
}
if(log){
return(list(x=x,x.log=x.log))
}else{
return(list(x=x,x.log=matrix(0,0,ncol(A))))
}
}
my.inv.pow.2 <- function(A,n.iter=3,b=rep(1,ncol(A)),log=FALSE){
x <- b
if(log){
x.log <- matrix(0,n.iter+1,ncol(A))
x.log[1,] <- x
}
for(i in 1:n.iter){
x2 <- solve(A,x)
x <- x2/sqrt(sum(x2^2))
if(log){
x.log[i+1,] <- x
}
}
if(log){
return(list(x=x,x.log=x.log))
}else{
return(list(x=x,x.log=matrix(0,0,ncol(A))))
}
}
tmp.Es.v <- list()
for(i in 1:4){
tmp.Es.v[[i]] <- sparseVector(rnorm(16),i=1:16,length=16)
}
N <- 20
X <- matrix(rnorm(N^2),N,N)
b <- rnorm(N)
tmp.outs <- my.inv.pow(X,n.iter=100,b=b,log=TRUE)
tmp.outs.2 <- my.inv.pow(X,n.iter=100,b=b,log=TRUE)
matplot(tmp.outs[[2]],type="l")
Es.v <- make.E.v(vertices,faces.v,rho)
E.re <- my.qMtorM(Es.v)
lambda <- my.inv.pow.2(E.re,n.iter=3)[[1]]
plot(lambda)
my.make.L <- function(vertices,faces.v){
n.v <- length(vertices)
L <- sparseVector(c(0),i=c(1),length=n.v^2)
for(i in 1:3){
v.ord <- ((1:3)+i+1) %% 3 + 1
k1 <- faces.v[v.ord[1],]
k2 <- faces.v[v.ord[2],]
k3 <- faces.v[v.ord[3],]
v1 <- vertices[k1]
v2 <- vertices[k2]
v3 <- vertices[k3]
u1 <- v2-v1
u2 <- v3-v1
u12 <- u1 * u2
cotAlpha <- (-Re(u12))/Mod(Im(u12))
addrk2k2 <- k2 + (k2-1)*n.v
addrk3k3 <- k3 + (k3-1)*n.v
addrk2k3 <- k2 + (k3-1)*n.v
addrk3k2 <- k3 + (k2-1)*n.v
addr <- c(addrk2k2,addrk3k3,addrk2k3,addrk3k2)
val <- c(cotAlpha,cotAlpha,-cotAlpha,-cotAlpha)/2
tmp.out <- my.vector.access(val,addr)
L <- L + sparseVector(tmp.out[[2]][,1],tmp.out[[1]],n.v^2)
}
L
}
L <- my.make.L(vertices,faces.v)
my.make.omega <- function(vertices,faces.v,lambda){
n.v <- length(vertices)
omega <- rep(0*Hi,n.v)
for(i in 1:3){
v.ord <- ((1:3)+i+1) %% 3 + 1
k1 <- faces.v[v.ord[1],]
k23 <- rbind(faces.v[v.ord[2],],faces.v[v.ord[3],])
k23 <- apply(k23,2,sort)
k2 <- k23[2,]
k3 <- k23[1,]
v1 <- vertices[k1]
v2 <- vertices[k2]
v3 <- vertices[k3]
edge <- v3-v2
lambda.mat <- matrix(lambda,nrow=4)
lambda.q <- as.quaternion(lambda.mat)
lambda.mat.2 <- lambda.mat
lambda.mat.2[2:4,] <- -lambda.mat.2[2:4,]
lambda.q. <- as.quaternion(lambda.mat.2)
lambda1 <- lambda.q[k2]
lambda1. <- lambda.q.[k2]
lambda2 <- lambda.q[k3]
lambda2. <- lambda.q.[k3]
val <- 1/3 * lambda1. * edge * lambda1 + 1/6 * lambda1. * edge * lambda2 + 1/6 * lambda2. * edge * lambda1 + 1/3 * lambda2. * edge * lambda2
u1 <- v2-v1
u2 <- v3-v1
u12 <- u1 * u2
cotAlpha <- (-Re(u12))/Mod(Im(u12))
Val <- cotAlpha * val /2
Val.m <- t(as.matrix(Val))
tmp.out2 <- my.vector.access(-Val.m,k2)
tmp.out3 <- my.vector.access(Val.m,k3)
omega[tmp.out2[[1]]] <- omega[tmp.out2[[1]]] + as.quaternion(t(tmp.out2[[2]]))
omega[tmp.out3[[1]]] <- omega[tmp.out3[[1]]] + as.quaternion(t(tmp.out3[[2]]))
}
omega.re <- as.matrix(omega)
omega.re <- omega.re-apply(omega.re,1,mean)
c(omega.re)
}
lambda.q <- as.quaternion(matrix(lambda,nrow=4))
omega <- my.make.omega(vertices,faces.v,lambda)
L.q <- list()
L.q[[1]] <- L
for(i in 2:4){
L.q[[i]] <- L*0
}
L.re <- my.qMtorM(L.q)
new.vertices <- solve(L.re,omega)
new.vertices <- as.quaternion(matrix(new.vertices,nrow=4))
newVertices <- matrix(new.vertices,nrow=4)[2:4,]
library(rgl)
plot3d(t(as.matrix(vertices)[2:4,]))
open3d()
plot3d(t(as.matrix(new.vertices)[2:4,]))
