2014-06-09

1. Concerning 'Whole' and 'Straight' ぱらぱらめくる『The Vortex of Life』

ぱらぱらめくるシリーズ射影幾何 Collineation Polar opposite 極変換双対 R

1. Concerning 'Whole' and 'Straight'
生物の理解のために「全体」を見よう
「まっすぐ」で理解する。「まっすぐ」な世界には、点、直線、平面…があり、線形代数がある。そしてそういうまっすぐなものは、変数は１乗であって、複数の変数の積は許さない。
(つまり、射影幾何で生物の複雑な形態を見ようというのは、多変数の(単純な)相加モデルが背後にあるものとして、その「現れ方」が射影になっているから、多彩な形ができている、と考えてみよう、ということ)
Collineation: 共線変換　は直線を直線に写し、直線の交点は写した先でも交点であるような変換

my.line <- function(v1,v2,t=seq(from=0,to=1,length=100)){
	matrix(1-t,ncol=1) %*% matrix(v1,nrow=1) + matrix(t,ncol=1) %*% matrix(v2,nrow=1)
}

my.circle <- function(r=1,ctr=c(0,0),t=seq(from=0,to=1,length=100),k=NULL){
	x <- r*cos(t*2*pi)
	y <- r*sin(t*2*pi)
	X <- matrix(0,length(t),length(ctr))
	X[,1] <- x
	X[,2] <- y
	X <- t(t(X) + ctr)
	if(!is.null(k)){
		b <- base.v(k)
		X <- t(b %*% t(X))
	}
	X
}

# あるベクトルを１つの軸とする正規直交基底
# vは接ベクトル
base.v <- function(v){
# 次元d
	d <- length(v)
# 単位ベクトル化
	v <- v/sqrt(sum(v^2))
	ret <- matrix(0,d,d)
# 第１列は接ベクトルそのもの
# 第２列以降は次の通り
# 第i列については、1,2,...,(i-1)行の成分はvの1,2,...,(i-1)成分に
# 比例した値としておき
# 第i行成分を接ベクトルと直交するための調節成分とする
# このようにすると、求めたいn-1個のベクトルと接ベクトルとの内積の計算と
# 求めたいn-1個のベクトル同士の内積の計算とが、同じになるので、
# 求めたいベクトルの値を接ベクトルとの関係で求めると、
# 漏れなく、他のベクトルとの関係も調整されることを使う
	for(i in 2:(d)){
		ret[1:(i-1),i] <- v[1:(i-1)]
		ret[i,i] <- -sum(v[1:(i-1)]^2)/v[i]
	}
	ret[,1] <- v
# 最後にノルムをそろえて回転行列化する
	q <- sqrt(apply(ret^2,2,sum))
	t(t(ret)/q)
}

v1 <- c(0.5,0)
v2 <- c(0,sqrt(3)/2)
v3 <- c(-0.5,0)
L1 <- my.line(v1,v2)
L2 <- my.line(v2,v3)
L3 <- my.line(v3,v1)
L123 <- rbind(L1,L2,L3)
plot(L123,type="l",asp=TRUE)

r <- sqrt(3)/6
ctr <- c(0,r)
C1 <- my.circle(r,ctr)
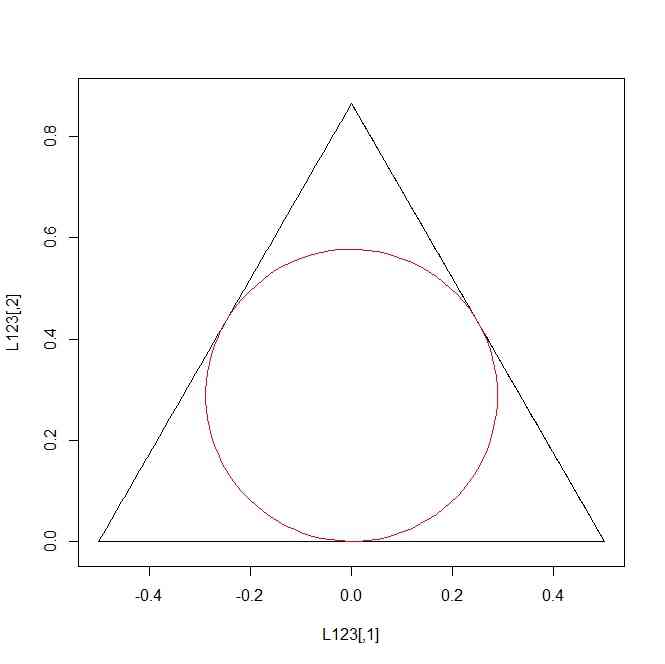
plot(L123,type="l",asp=TRUE)
points(C1,type="l",col=2)

# Linear 

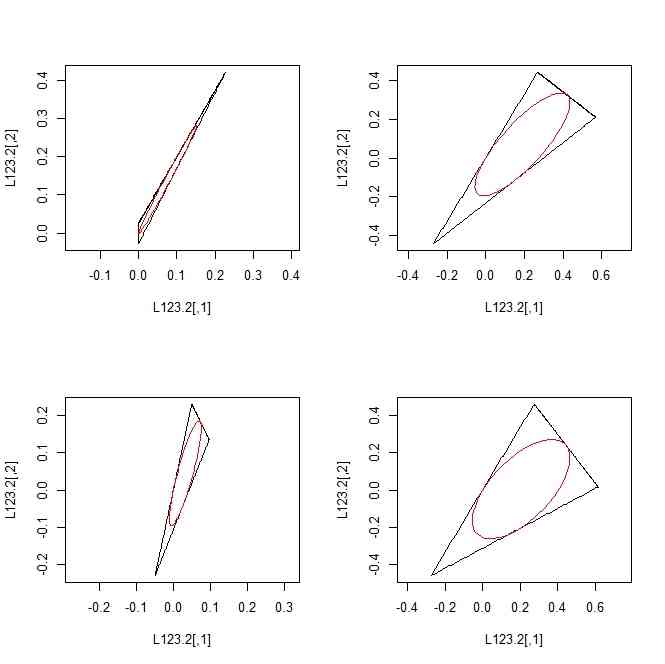
par(mfcol=c(2,2))
for(i in 1:4){
M <- matrix(runif(4),2,2)
L123.2 <- t(M %*% t(L123))
C1.2 <- t(M %*% t(C1))
plot(L123.2,type="l",asp=TRUE)
points(C1.2,type="l",col=2)
}
par(mfcol=c(1,1))

# Quadratic
# y座標をx,yの二次式で変形
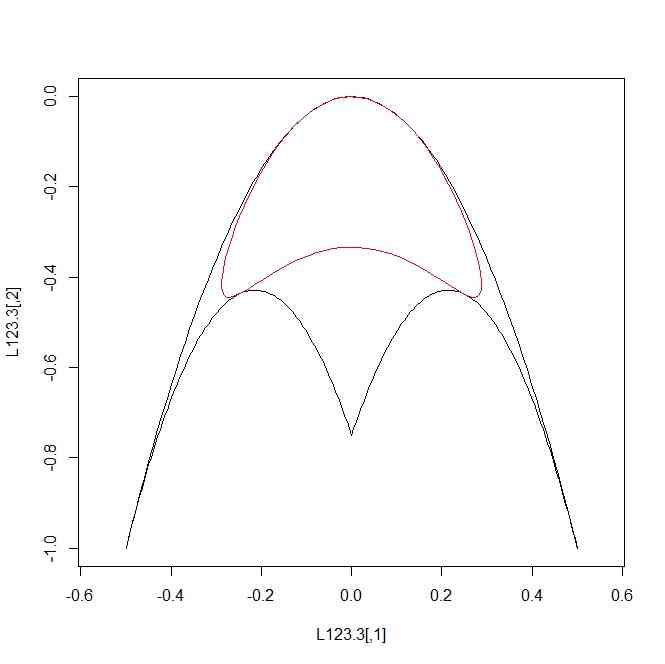
tmp.f <- function(x){-(x[,2])^2-4*x[,1]^2}
L123.3 <- L123
L123.3[,2] <- tmp.f(L123.3)
C1.3 <- C1
C1.3[,2] <- tmp.f(C1.3)
plot(L123.3,type="l",asp=TRUE)
points(C1.3,type="l",col=2)

Polar oppositeとpolar transformation
- 点、直線、平面、…、超平面
- 点と一番高次の超平面はひっくり返せる(双対性)
- そのひっくり返した「相方」をpolar oppositeと呼び、その「ひっくり返し処理」をpolar transformationと呼ぶ
- 一般に、d次元空間では二次曲面(二次関数で表される超曲面)が(d+1)x(d+1)行列Aとd次元ベクトルxに1を付け加えてd+1次元ベクトルとしたXとを使って $X^T A X=0$ と表せる
- たとえば半径１の球面の場合、Aは単位行列とほぼ同じで、(d+1,d+1)成分が-1であるようなそれである
- このときd次元ベクトルpという点に対して $(x,1)^T A (p,1)=0$ なる超平面との関係を極変換双対関係という
- 参考はこちら

# 極対応
# 極変換の基準は原点を中心とした半径rの円
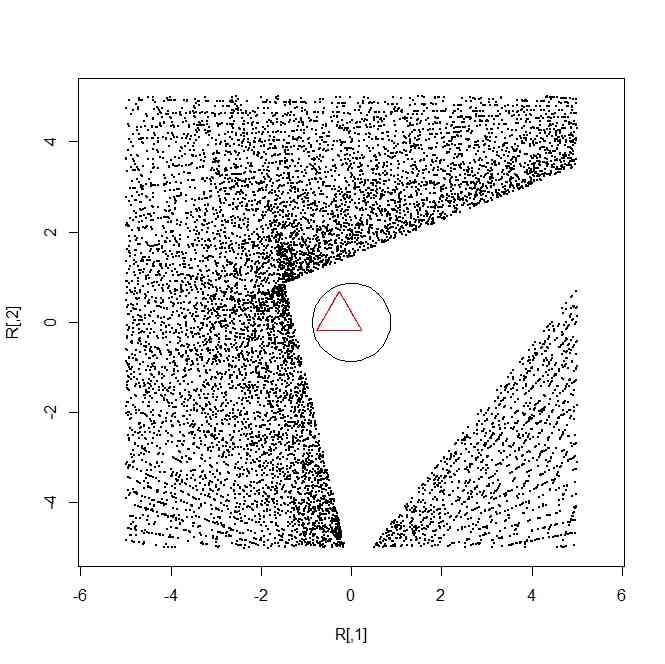
r <- sqrt(3)/6*3
# この極変換の「対応を決める行列」
A <- diag(c(rep(1,2),-1)) * r
# 正三角形を上記の円の内側のそれにして、中心が原点からずれるように適当に動かす
Tri <- L123 
Tri[,1] <- Tri[,1] + rnorm(1)*0.2
Tri[,2] <- Tri[,2] - sqrt(3)/6 + rnorm(1)*0.2
C2 <- my.circle(r)
#plot(C2,type="l",asp=TRUE)
#points(Tri,type="l",col=2)
# たくさんの乱点を発生する
n.pt <- 100000
R <- matrix((runif(n.pt*2)-0.5)*10,ncol=2)
# 極変換のために、第３要素１を加える
tmp.R <- cbind(R,rep(1,n.pt))
#plot(R,pch=20,cex=0.1,asp=TRUE)
#points(C2,type="l")
#points(Tri,type="l",col=2)
# 三角形の座標にも第３要素を加える
tmp.Tri <- cbind(Tri,rep(1,length(Tri[,1])))
# 乱点のそれぞれに対して、三角形上の点のすべてとに関してx A p を計算する
V <- tmp.R %*% A %*% t(tmp.Tri)
# x A pの値が0のものが「ＯＫ」な点なので、三角形のどの点とでもよいのでかなり0に近いかどうかを調べる
min.V <- apply(abs(V),1,min)
s <- which(min.V < quantile(min.V,0.1))
col <- rep(0,n.pt)
col[s] <- 1
plot(R,pch=20,cex=0.1,asp=TRUE,col=col)
points(C2,type="l")
points(Tri,type="l",col=2)