京大２次試験数学問題をRで表現する

• 昨日、二次試験前期の第一日目があり、数学の試験問題がウェブ上に出ました(こちら)
• Rでなぞってみます
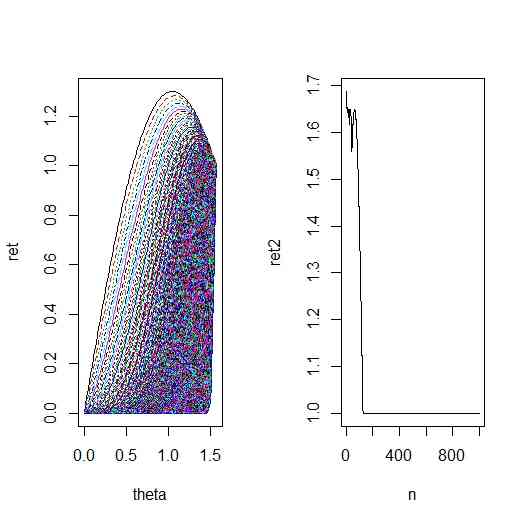
• (1) n >= 2 自然数。のにおける最大値をとする。を求めよ。を求めよ

#n <- 2^(seq(from=1,to=10,length=100))
n <- seq(from=2,to=1000,length=10000)
theta <- seq(from=0,to=pi/2,length=100)
ret <- matrix(0,length(theta),length(n))
ret2 <- rep(NA,length(n))
for(i in 1:length(n)){
	ret[,i] <- (1+cos(theta)) * sin(theta)^(n[i]-1)
	ret2[i] <- max(ret[,i])^n[i]
}
par(mfcol=c(1,2))
matplot(theta,ret,type="l")
plot(n,ret2,type="l")
par(mfcol=c(1,1))

• (2) 素数p,qを用いてと表される素数をすべて挙げる
  • 素数の列挙

primes <- c(2)
max.val <- 1000
for(i in 3:max.val) {
	if(length(primes)>0){
		tmp <- i %% primes
		if(prod(tmp)!=0){
			primes <- c(primes,i)
		}
	}
}
primes

• • 素数判定

## 素数判定
is.prime <- function(x){
	ret <- FALSE
	if(x==2){
		ret <- TRUE
	}
	if(x > 2){
		tmp <- x %% (2:(x-1))
		if(prod(tmp!=0)){
			ret <- TRUE
		}
	}
	return(ret)
}

is.prime(1)
is.prime(2)
is.prime(10)
is.prime(11)

• • 偶奇性から、p,qのうちの１つは2
  • p=2として,３以上の素数をqとして、の素数判定をしてみる
  • 「計算機で列挙する」作戦と、「ないことを証明する作戦」は相性が悪いが…

primes <- c(2)
max.val <- 20
for(i in 3:max.val) {
	if(length(primes)>0){
		tmp <- i %% primes
		if(prod(tmp)!=0){
			primes <- c(primes,i)
		}
	}
}
primes
ret <- c()
ret2 <- c()

for(i in primes){
	tmp <- 2^i + i^2
	if(is.prime(tmp)){
		ret <- c(ret,i)
		ret2 <- c(ret2,tmp)
	}
}

> primes
[1]  2  3  5  7 11 13 17 19
> ret <- c()
> ret2 <- c()
> 
> for(i in primes){
+ tmp <- 2^i + i^2
+ if(is.prime(tmp)){
+ ret <- c(ret,i)
+ ret2 <- c(ret2,tmp)
+ }
+ }
> ret
[1] 3
> ret2
[1] 17

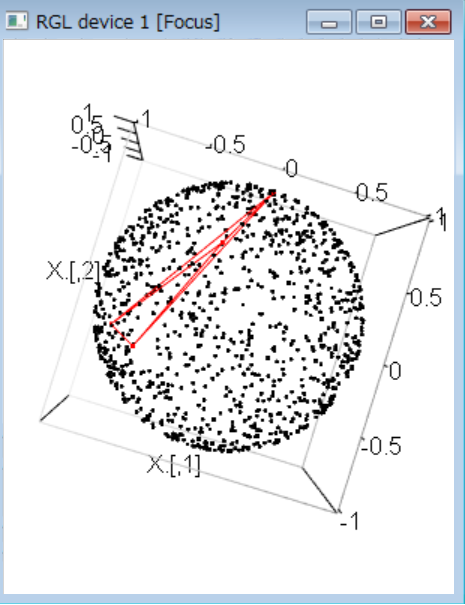
• (3) 正四面体の頂点座標を計算する代わりに、４次元空間を考えて(1,0,0,0),(0,1,0,0),(0,0,1,0),(0,0,0,1)の４点を取ると、これは正四面体の４頂点。また、四面体を単位球上の４点と見ることで、一般的な四面体と、各面の外接円とが表現できる。外接円の中心は、三角形を乗せている面に、外接球の中心からの垂線の足

n <- 4
x <- matrix(rnorm(4*3),ncol=3)
tmp <- sqrt(apply(x^2,1,sum))
x. <- x/tmp
X <- matrix(rnorm(1000*3),ncol=3)
tmp2 <- sqrt(apply(X^2,1,sum))
X. <- X/tmp2
library(rgl)
plot3d(X.)
points3d(x.,col=2)
segments3d(x.[c(1,2,1,3,1,4,2,3,2,4,3,4),],col=2)

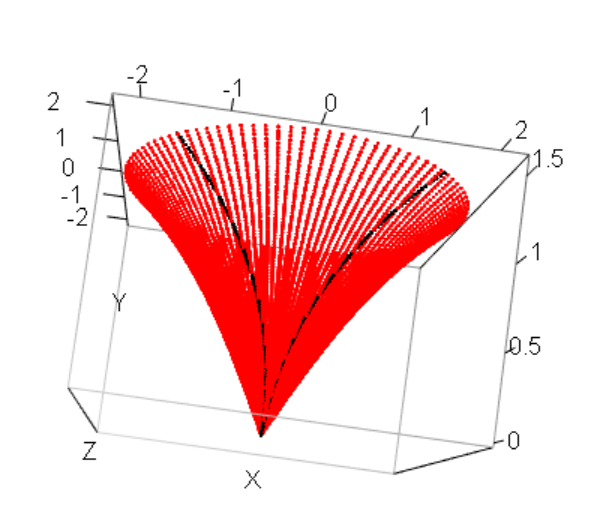
• (4) 3次元空間。y=z平面。という領域Dをy軸上に回転

a <- 1.6
y <- seq(from=0,to=a,length=100)
x1 <- (exp(y)+exp(-y))/2 -1
x2 <- -x1

X <- c(x1,x2)
Y <- c(y,y)
Z <- Y

plot3d(X,Y,Z)

XZ.len <- sqrt(X^2 + Z^2)

theta <- seq(from=0,to=1,length=100)*2*pi

for(i in 1:length(theta)){
	X. <- XZ.len * cos(theta[i])
	Z. <- XZ.len * sin(theta[i])
	points3d(X.,Y,Z.,col=2)
}

• (5) 単位正方形を横に２つ並べた６頂点のランダムウォーク

# v1 =(0,0),v2=(1,0),v3=(2,0),v4=(0,1),v5=(0,2),v6=(0,3)とする
V <- matrix(c(0,0,1,0,2,0,0,1,0,2,0,3),byrow=TRUE,ncol=2)
V
# 各点の距離をマンハッタン距離で測る
D <- as.matrix(dist(V,"manhattan"))
# 距離１の箇所を取り出す
D. <- D==1
D.sum <- apply(D.,1,sum)
# 推移行列
M <- t(D./D.sum)

# ステップ数
n <- 20

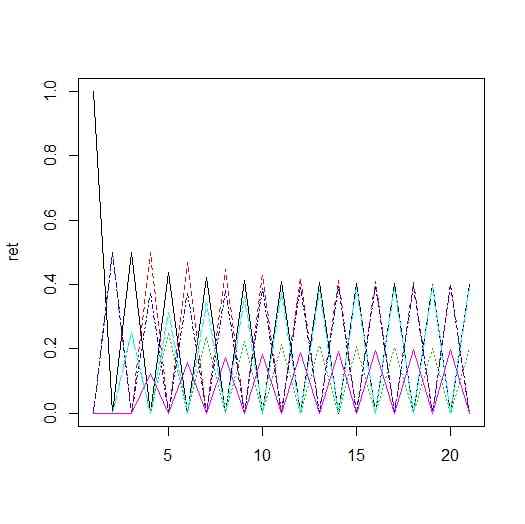
ret <- matrix(0,n+1,6)
ret[1,] <- c(1,0,0,0,0,0) # 初期状態では確率１でv1=(0,0)に居る

for(i in 2:(n+1)){
	ret[i,] <- M %*% ret[i-1,]
}

matplot(ret,type="l")

• (6) 複素係数の２次式、複素関数の割り算。複素関数を「変形」と考えて、複素平面上の格子を関数によって変形してみる

my.complex.grid <- function(r0=-3,r1=3,i0=-3,i1=3,n1=5,n2=50){
	re1 <- seq(from=r0,to=r1,length=n1)
	im1 <- seq(from=i0,to=i1,length=n1)
	re2 <- seq(from=r0,to=r1,length=n2)
	im2 <- seq(from=i0,to=i1,length=n2)
	ret <- rbind(as.matrix(expand.grid(re1,im2)),as.matrix(expand.grid(re2,im1)))
	return(ret[,1]+1i*ret[,2])
}

gr <- my.complex.grid()

my.f <- function(x,a,b){
	x^2 + a*x + b
}

par(mfcol=c(1,2))
a <- 2+1i*3
b <- 1i * 2
plot(my.f(gr,a,b),pch=20,cex=0.1)
plot(my.f(gr^3,a,b),pch=20,cex=0.1)
par(mfcol=c(1,1))