- 少し慣れてきたので、なぞった内容をもう少しいじってみる
import numpy as np # ベクトル・行列・高次元アレイを使う
import scipy as sp # 線形代数・関数・数値計算
# matplotlibのpylabインタフェースは、MATLABの利用経験があるユーザがmatplotlibを簡単に習得できるように設計されている。というわけで以下2つを入れる
import matplotlib as mp
import pylab as pl
import os # コンピュータのファイルの出し入れのため
os.chdir('C:\\Users\\ryamada\\Desktop\\python') # Windowsでは'\'が'\\'になることに注意
from numpy import array
n = 100
#t = np.linspace(0,1,n) * 2 * np.pi
t = np.arange(n) * 2 * np.pi/n
n_circ = 4
Rs = [1.0,0.1,0.15,0.2]
Xs = [0.,0.6,-0.5,0]
Ys = [0.,-0.4,-0.1,0]
output = {'vertices': None, 'holes': None, 'segments': None}
vertices = []
segments = []
holes = []
for i in range(n_circ) :
tmpx = Xs[i]
tmpy = Ys[i]
tmpr = Rs[i]
x = tmpr * sp.cos(t) + tmpx
y = tmpr * sp.sin(t) + tmpy
for i2 in range(n) :
vertices.append([float(x[i2]), float(y[i2])])
tmp = i2-1
if(i2==0) :
tmp = n-1
segments.append([tmp+n*i,i2+n*i])
N_holes = n_circ-1
for k in range(N_holes):
tmpx = Xs[k+1]
tmpy = Ys[k+1]
holes.append([tmpx,tmpy])
output['vertices']=np.array(vertices)
output['segments']=np.array(segments)
output['holes']=np.array(holes)
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt
%matplotlib inline
lake_superior = output
vertices_ls = lake_superior['vertices']
vertices_ls.shape
%time hull = ConvexHull(vertices_ls)
plt.figure(figsize=(8, 8)) # 図のサイズ指定
plt.xlim(vertices_ls[:,0].min()-0.01, vertices_ls[:,0].max()+0.01) # x,y軸の範囲を存在点座標の範囲より0.01広げる
plt.ylim(vertices_ls[:,1].min()-0.01, vertices_ls[:,1].max()+0.01)
plt.axis('off')
plt.axes().set_aspect('equal') # x,y軸の長さを揃える
plt.plot(vertices_ls[:,0], vertices_ls[:,1], 'b.')
for simplex in hull.simplices: # hull.simplicesの要素(辺)を一つずつ描く
plt.plot(vertices_ls[simplex, 0], vertices_ls[simplex, 1], 'r-')
plt.show()
from scipy.spatial import Voronoi, voronoi_plot_2d
vor = Voronoi(vertices_ls)
plt.figure(figsize=(10, 10))
ax = plt.subplot(111, aspect='equal')
voronoi_plot_2d(vor, ax=ax)
plt.xlim(-3,3) # 範囲は、適当に描かれた絵を見たあとで調整使用
plt.ylim(-3,3)
plt.show()
from scipy.spatial import Delaunay, delaunay_plot_2d
tri = Delaunay(vertices_ls)
plt.figure(figsize=(10, 10))
ax = plt.subplot(111, aspect='equal')
delaunay_plot_2d(tri, ax=ax)
plt.show()
from triangle import triangulate, plot as tplot
cndt = triangulate(lake_superior, 'p')
plt.figure(figsize=(10, 10))
ax = plt.subplot(111, aspect='equal')
tplot.plot(ax, **cndt)
plt.show()
cfdt = triangulate(lake_superior, 'pD')
plt.figure(figsize=(10, 10))
ax = plt.subplot(111, aspect='equal')
tplot.plot(ax, **cfdt)
plt.show()
#cncfq50 = triangulate(lake_superior, 'q90')
#plt.figure(figsize=(18,18))
#ax = plt.subplot(111, aspect='equal')
#tplot.plot(ax, **cncfq50)
#plt.show()
cncfq20adt = triangulate(lake_superior, 'pq20a.1D')
plt.figure(figsize=(18, 18))
ax = plt.subplot(111, aspect='equal')
tplot.plot(ax, **cncfq20adt)
plt.show()
from scipy.spatial import minkowski_distance
X = cncfq20adt['triangles'][:,0]
Y = cncfq20adt['triangles'][:,1]
Z = cncfq20adt['triangles'][:,2]
Xvert = [cncfq20adt['vertices'][x] for x in X]
Yvert = [cncfq20adt['vertices'][y] for y in Y]
Zvert = [cncfq20adt['vertices'][z] for z in Z]
lengthsXY = minkowski_distance(Xvert, Yvert)
lengthsXZ = minkowski_distance(Xvert, Zvert)
lengthsYZ = minkowski_distance(Yvert, Zvert)
from scipy.sparse import lil_matrix
from scipy.sparse.csgraph import shortest_path
nvert = len(cncfq20adt['vertices'])
G = lil_matrix((nvert, nvert))
for k in range(len(X)):
G[X[k], Y[k]] = G[Y[k], X[k]] = lengthsXY[k]
G[X[k], Z[k]] = G[Z[k], X[k]] = lengthsXZ[k]
G[Y[k], Z[k]] = G[Z[k], Y[k]] = lengthsYZ[k]
dist_matrix, pred = shortest_path(G, return_predecessors=True, directed=True, unweighted=False)
index = 90 # ウェブサイトで使っている指定番地では数が大きすぎるので適当な数を入れる
path = [90] # 同上
while index != 40: # ウェブサイトで使っている指定番地では数が大きすぎるので適当な数を入れる
index = pred[40, index] # 同上
path.append(index)
Xs = [cncfq20adt['vertices'][x][0] for x in path]
Ys = [cncfq20adt['vertices'][x][1] for x in path]
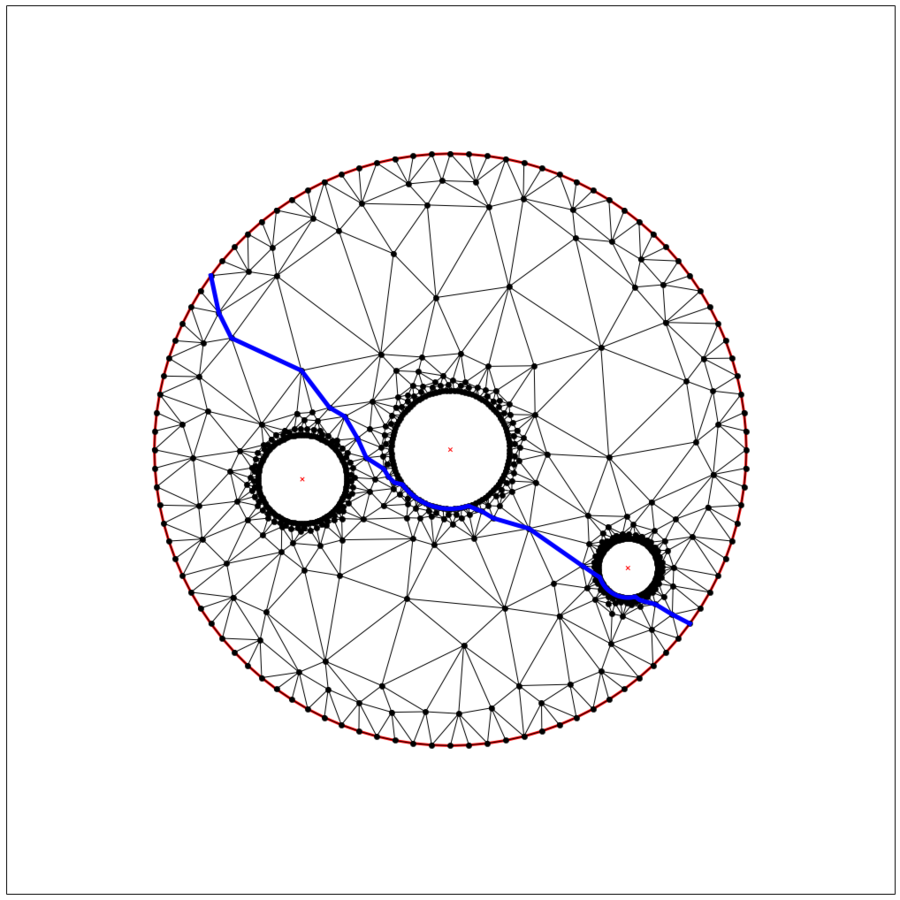
plt.figure(figsize=(18,18))
ax = plt.subplot(111, aspect='equal')
tplot.plot(ax, **cncfq20adt)
ax.plot(Xs, Ys, '-', linewidth=5, color='blue'); \
plt.show()

import numpy as np # ベクトル・行列・高次元アレイを使う
import scipy as sp # 線形代数・関数・数値計算
# matplotlibのpylabインタフェースは、MATLABの利用経験があるユーザがmatplotlibを簡単に習得できるように設計されている。というわけで以下2つを入れる
import matplotlib as mp
import pylab as pl
import os # コンピュータのファイルの出し入れのため
os.chdir('C:\\Users\\ryamada\\Desktop\\python') # Windowsでは'\'が'\\'になることに注意
#from numpy import array
R = 1
n = 100
#t = np.linspace(0,1,n) * 2 * np.pi
t = np.arange(n) * 2 * np.pi/n
t2 = np.arange(n) * 1.9 * np.pi/n
t3 = np.arange(n) * 1.5 * np.pi/n
x = R * sp.cos(t) + R*0.2 * sp.cos(t*4+np.pi/5)
y = R * sp.sin(t) + R *0.2* sp.sin(t*4)
mp.pyplot.plot(x,y)
mp.pyplot.xlim(x.min()-0.01, x.max()+0.01) # x,y軸の範囲を存在点座標の範囲より0.01広げる
mp.pyplot.ylim(y.min()-0.01, y.max()+0.01)
mp.pyplot.axis('off')
mp.pyplot.axes().set_aspect('equal') # x,y軸の長さを揃える
mp.pyplot.plot(x,y, 'b.')
R2 = 0.3
ctr_2x = 0.2
ctr_2y = 0.1
x2 = R2 * sp.cos(t2) + ctr_2x + R2*0.1 * sp.cos(t2*4+np.pi/5)
y2 = R2 * sp.sin(t2) + ctr_2y + R2*0.1 * sp.sin(t2*4+np.pi/5)
R3 = 0.1
ctr_3x = 0.25
ctr_3y = 0.11
x3 = R3*2 * sp.cos(t3) + ctr_3x
y3 = R3 * sp.sin(t3) + ctr_3y
output = {'vertices': None, 'holes': None, 'segments': None}
vertices = []
for i in range(n) :
vertices.append([float(x[i]), float(y[i])])
for i in range(n) :
vertices.append([float(x2[i]), float(y2[i])])
for i in range(n) :
vertices.append([float(x3[i]), float(y3[i])])
output['vertices']=np.array(vertices)
segments = []
for i in range(n) :
tmp = i-1
if(i==0) :
tmp = n-1
segments.append([tmp,i])
for i in range(n) :
tmp = i-1
if(i==0):
tmp = n-1
segments.append([n+tmp, n+i])
for i in range(n) :
tmp = i-1
if(i==0):
tmp = n-1
segments.append([2*n+tmp, 2*n+i])
segments[n][0] = n*2
segments[2*n][1] = 2*n-1
output['segments']=np.array(segments)
holes = []
N_holes = 1
for k in range(N_holes):
holes.append([ctr_3x+R3*1.2, ctr_3y + R3*1.2])
output['holes'] = np.array(holes)
from scipy.spatial import ConvexHull
import matplotlib.pyplot as plt
%matplotlib inline
lake_superior = output
vertices_ls = lake_superior['vertices']
vertices_ls.shape
%time hull = ConvexHull(vertices_ls)
plt.figure(figsize=(18, 18)) # 図のサイズ指定
plt.xlim(vertices_ls[:,0].min()-0.01, vertices_ls[:,0].max()+0.01) # x,y軸の範囲を存在点座標の範囲より0.01広げる
plt.ylim(vertices_ls[:,1].min()-0.01, vertices_ls[:,1].max()+0.01)
plt.axis('off')
plt.axes().set_aspect('equal') # x,y軸の長さを揃える
plt.plot(vertices_ls[:,0], vertices_ls[:,1], 'b.')
for simplex in hull.simplices: # hull.simplicesの要素(辺)を一つずつ描く
plt.plot(vertices_ls[simplex, 0], vertices_ls[simplex, 1], 'r-')
plt.show()
from scipy.spatial import Voronoi, voronoi_plot_2d
vor = Voronoi(vertices_ls)
plt.figure(figsize=(10, 10))
ax = plt.subplot(111, aspect='equal')
voronoi_plot_2d(vor, ax=ax)
plt.xlim(-3,3) # 範囲は、適当に描かれた絵を見たあとで調整使用
plt.ylim(-3,3)
plt.show()
from scipy.spatial import Delaunay, delaunay_plot_2d
tri = Delaunay(vertices_ls)
plt.figure(figsize=(18, 18))
ax = plt.subplot(111, aspect='equal')
delaunay_plot_2d(tri, ax=ax)
plt.show()
from triangle import triangulate, plot as tplot
cndt = triangulate(lake_superior, 'p')
plt.figure(figsize=(18, 18))
ax = plt.subplot(111, aspect='equal')
tplot.plot(ax, **cndt)
plt.show()
cncfq20adt = triangulate(lake_superior, 'pq20a.001D')
plt.figure(figsize=(18, 18))
ax = plt.subplot(111, aspect='equal')
tplot.plot(ax, **cncfq20adt)
plt.show()
from scipy.spatial import minkowski_distance
X = cncfq20adt['triangles'][:,0]
Y = cncfq20adt['triangles'][:,1]
Z = cncfq20adt['triangles'][:,2]
Xvert = [cncfq20adt['vertices'][x] for x in X]
Yvert = [cncfq20adt['vertices'][y] for y in Y]
Zvert = [cncfq20adt['vertices'][z] for z in Z]
lengthsXY = minkowski_distance(Xvert, Yvert)
lengthsXZ = minkowski_distance(Xvert, Zvert)
lengthsYZ = minkowski_distance(Yvert, Zvert)
from scipy.sparse import lil_matrix
from scipy.sparse.csgraph import shortest_path
nvert = len(cncfq20adt['vertices'])
G = lil_matrix((nvert, nvert))
for k in range(len(X)):
G[X[k], Y[k]] = G[Y[k], X[k]] = lengthsXY[k]
G[X[k], Z[k]] = G[Z[k], X[k]] = lengthsXZ[k]
G[Y[k], Z[k]] = G[Z[k], Y[k]] = lengthsYZ[k]
dist_matrix, pred = shortest_path(G, return_predecessors=True, directed=True, unweighted=False)
st_v = np.random.choice(range(3*n),50)
end_v = np.random.choice(range(3*n),50)
cols = np.random.choice(['b','g','r','c','y'],50)
plt.figure(figsize=(18,18))
ax = plt.subplot(111, aspect='equal')
tplot.plot(ax, **cncfq20adt)
for i in range(len(st_v)) :
index = st_v[i] # ウェブサイトで使っている指定番地では数が大きすぎるので適当な数を入れる
path = [st_v[i]] # 同上
while index != end_v[i]: # ウェブサイトで使っている指定番地では数が大きすぎるので適当な数を入れる
index = pred[end_v[i], index] # 同上
path.append(index)
Xs = [cncfq20adt['vertices'][x][0] for x in path]
Ys = [cncfq20adt['vertices'][x][1] for x in path]
tmp_col = np.random.rand(3,1)/2 + 0.5
ax.plot(Xs, Ys, '-', linewidth=5, color=cols[i]); \
plt.show()

