2014-11-06

Circle packing

Circle packingというのがある。同じ単語で異なる複数の概念に対応するようなので、注意が必要だが、ここでは共形変換とのからみで使うそれを扱う

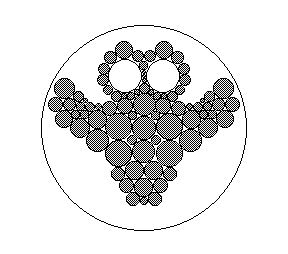
$http://www.math.utk.edu/~kens/Owl0.gif$

具体的には、このPDFにあるようなそれのこと
共形変換では「角保存」するわけだけれど、それは「直角は直角」のことで、そうすると、円の接線、円と円の接し方も保存されることになる
そのことを利用して、ユークリッド平面ならば、同じ大きさの円の敷き詰めをすると、一つの円の周囲に６個の円が接するわけだけれど、非ユークリッドな歪みのある幾何を考えると、円の周囲に６個とは限らない円が接することになる。そのようにして敷き詰めるためには、もちろん円の大きさを変えないといけない
共形変換では、一つながりの穴のない任意の領域が単位円板に変換できるが、その変換の具合というのが
- 単位円板に敷き詰めた大きさの異なる円
- 同じサイズの円を敷き詰めた、任意領域
という２つの間で、「円のふれあい関係」が同じ、という対応付けをすることができる
これを使って、共形変換の近似をしよう、というのが、共形変換とCircle packingとの関係
これをするアプリケーションはCとJavaとで実装されており、冒頭のPDFに記載されているURLから取れるわけだが、ここでは、少し違うことをしてみることとする
領域の外周に着目する
出っ張った部分は、単位円板では小さい円が密に並び、逆に凹んだ部分は大きい円が並ぶ
これは、領域の内部を意識して、外周に向きを考えたときに生じる、正負を考慮した曲率(曲率半径)と、領域に敷き詰めた同サイズの円の個数（外周に沿って並ぶ個数)との関係のせいである
Circle packingでは、有限個の円の敷き詰めで考えるわけだけれど、曲率と、並ぶ円の個数の「比」について考えるだけなら、敷き詰め用の円を無限小にしてもよさそうだから、その個数(敷き詰め密度)について、考えてみることにする
領域の外周が直線であるとする
- この直線に沿って、半径rの円を敷き詰めるとき、外周(今は直線)の長さLに対して、k個の円が並んでいるとすれば、 $L = 2kr$ 。したがって、単位長さあたりの円の個数は $\frac{1}{2r}$
領域の外周が外に凸で、その曲率半径がRだとする
- 局所的に曲率半径がRなわけだが、それがぐるりと１周しているとすれば、その外周の長さは $2\pi R$
- 今、その内側に半径rの円が並んでいるが、２つの相並ぶ半径rの円の中心が、この半径Rの円の中心に対してなす角を $2\theta$ とすれば、 $\sin(\theta) = \frac{r}{R-r}$
- したがって、並んでいる半径rの円の個数は、 $\frac{2\pi}{2\theta}$
- つまり、単位長さあたりの個数は $\frac{2\pi}{2asin{\frac{r}{R-r}}}/(2\pi R)=\frac{1}{2R asin{\frac{r}{R-r}}}$
領域の外周が凹で、その曲率半径がRだとする
- 凸の場合と同様に考えて $\frac{1}{2R asin{\frac{r}{R+r}}}$
これを、凸の場合のRを負にし、 $\frac{1}{R}$ を考えることで、凹凸の間に直線状を挟んだ形でパラメタとし、小円の個数を計算することができる

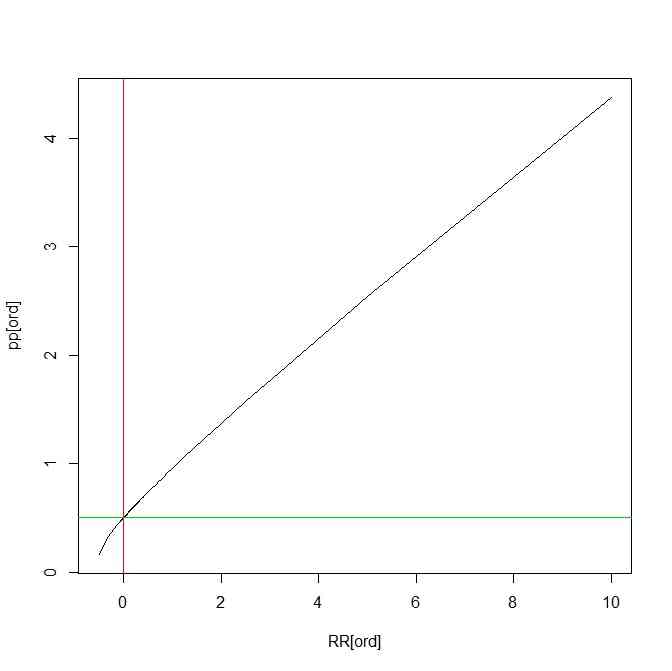
直線のときに0.5として、凸→凹に向かって、小円数が増えている様子が見てとれる
これを使うと、任意の2次元閉領域であって、外周に曲率が定められれば、それを単位円板に対応付けるときに、外周の凹凸の様子に応じて単位円板外周に粗密を決めて対応付けることができる(はず)

# 凹
R <- seq(from=0,to=1000,length=10000)
# 凸(曲率半径は、小円の半径の２倍以上とする)
R2 <- seq(from=2*r,to=1000,length=1000)
# 小円の半径を1として考える
r <- 1
p <- 1/(2*R*asin(r/(R+r)))
q <- 1/(2*R2*asin(r/(R2-r)))
RR <- c(1/R,-1/R2)
pp <- c(p,q)
ord <- order(RR)

plot(RR[ord],pp[ord],pch=20,type="l")
abline(v=0,col=2)
abline(h=0.5,col=3)