- Rの練習のための勉強会での話題
- フィボナッチ数列は1,1,2,3,5,8,...というやつで
- f(1)=1,f(2)=1,f(n)=f(n-1)+f(n-2);n>2というルールの漸化式で決まる整数列
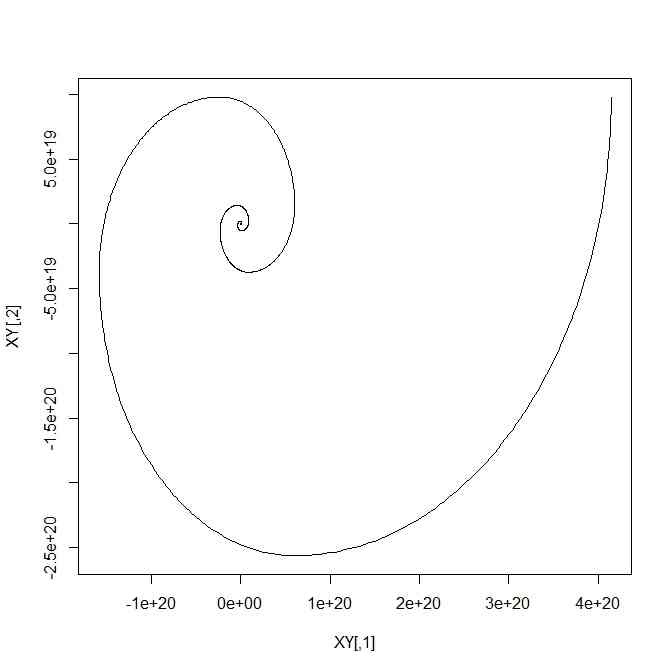
- そのルールを使うと、こんならせんが描ける
- そこには、フィボナッチ数を1辺の長さとする正方形による敷き詰めという背景がある(こちら)
- たしかにフィボナッチ数の長さを求めてからその長さを使った敷き詰めをすることはできる
- できるけど、貝がそんな計算をしているわけがない。平面座標用の「漸化式」があって、それに応じて巻いているに違いない
- ベクトルの漸化式を次のようにする
- 第1ベクトルは、始点をctr1=(0,0)とし、v1=(1,0)なるベクトルであるとする
- 第2ベクトルは、始点をctr2=(0,0)とし、v2=(0,1)なるベクトルであるとする
- 第3ベクトルは、始点をctr3=ctr2 + v1とし、v3=反時計回りに1/4回転(v2) - v1
- 第4ベクトルは、視点をctr4=ctr3 + v2とし、v4=反時計回りに1/4回転(v3) - v2
- 結局、ctr(1)=(0,0),ctr(2)=(0,0),v(1)=(1,0),v(2)=(0,1)でctr(n) = ctr(n-1) + v(n-2)、v(n) = R v(n-1) - v(n-2);Rは反時計回りに1/4回転
- もしくは、ctr(0)=(0,0),ctr(1)=(0,0),v(0)=(0,0),v(1)=(1,0)でctr(n) = ctr(n-1) + v(n-2)、v(n) = R v(n-1) - v(n-2);Rは反時計回りに1/4回転
R <- matrix(c(cos(pi/2),-sin(pi/2),sin(pi/2),cos(pi/2),byrow=TRUE,2,2)
n <- 100
ctrs <- matrix(0,n+1,2)
vs <- matrix(0,n+1,2);vs[2,] <- c(1,0)
for(i in 3:(n+1)){
ctrs[i,] <- ctrs[i-1,] + vs[i-2,]
vs[i,] <- c(R %*% v[i-1,]) - vs[i-2,]
}
R.angle <- function(theta){
matrix(c(cos(theta),-sin(theta),sin(theta),cos(theta)),byrow=TRUE,2,2)
}
theta <- seq(from=0,to=pi/2,length=100)
XY <- matrix(0,0,2)
for(i in 1:n){
tmp.XY <- matrix(0,length(theta),2)
for(j in 1:length(theta)){
tmp.XY[j,] <- R.angle(theta[j]) %*% vs[i,]
}
tmp.XY.2 <- t(t(tmp.XY) + ctrs[i,])
XY <- rbind(XY,tmp.XY.2)
}
plot(XY,type="l",asp=TRUE)
- ここではいわゆるフィボナッチ数を出す漸化式は使っていないけれど、生成ベクトルの長さを計算すると、フィボナッチ数列ができていることがわかる
sqrt(apply(vs^2,1,sum))[1:20]
- どうしてこれにフィボナッチ数列が隠れるかというと、「1/4回転」する、というのは、f(n)=f(n-1)+f(n-2)するときに、nとn-2とが1/2回転ずれていて、nとn-1とが1/4回転ずれているという状況を作った上で、n-1のずれをnとn-2とのずれの方向に持ってくるための操作だ、と考えればよい
