- 結び目、絡み目、その高次元をここ数日でメモしているのだが、さて。
- 円軌道を複数の要素が作るには、巡回行列的な連立微分方程式を作ればよい
- じゃあ、球系の結び目の連立微分方程式を作るとしたらどうする?(ここで言う微分方程式、というのは、変化量を要素で決定論的に定める、という意味であって、どういう形でそれが書けるのかについては、まったく白紙で考えておく)
- また、非球系ではどうなるかをやろうと思ったら、まずはトーラス軌道の連立微分方程式はどうなるかを確認して、その上で、そこに結び目を入れるには…となるだろう
- そして絡み目は結び目を複数合わせたものであって、「結び目どうしの関係」は、軌道を作る連立微分方程式を一塊とみて、その一塊の連立微分方程式が複数あって、その複数の連立微分方程式間に何かしらの相互作用を入れることになるが、それはどうする?
- 直接触れ合っていないけれども相互作用を及ぼす仕組みであって絡み目のようなものは「電場と磁場」とが、例として良く取り上げられるが、連立方程式が「場」において相互作用する、というような作りにする?
- さらに、「結び目」「絡み目」を1次元多様体が3次元多様体に埋め込まれたものとして上記は書いたが、これを、多次元化すると、「微分方程式」が「曲線」を作る微分方程式ではなくて、「微分多様体」みたいなそれになる…?
- ここに統計学的検定とかデータからの読み取りとかを持ち込むとすると、さらに「確率微分方程式」的な拡張をすることになる?
- その上で、「観測」とは、時間に関するスライスなのか経時的なそれなのかの選択も含めて、「射影」なので、「影」から元のモデルを推定するにあたっての、「射影」とは、「何」なのか、ということが問題になるのだろう
- 線形統計学っていうのは、この多様体上のもろもろのうち、多様体が局所では線形空間とみなせることから、その部分についての観察とモデル化をする、という仕事のことで、それは、埋め込まれたものも、埋め込みに使った空間も線形と見ているのだろう。他方、非線形解析っていうのは、もう少し、歪みにセンシティブなもののようだが、そうは言っても、それは埋め込まれた方の歪みについてのことであって、埋め込みに使った空間である多様体については局所線形性を仮定しているのだろうか。それとも、空間側の歪みにセンシティブでありつつ、埋め込まれた方は線形にしているのだろうか。微分方程式にしてみるとその違いがわかりそうな気がする
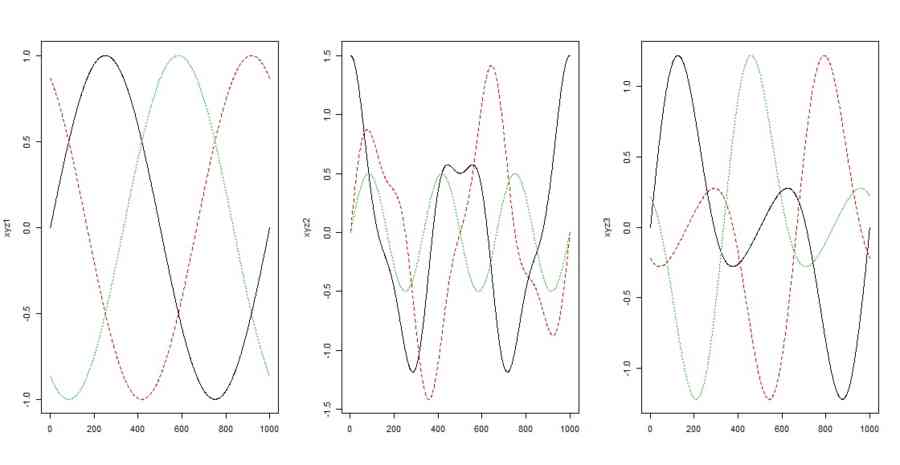
- 円はぐるぐる、トーラスはぐるぐるの上にぐるぐるが乗った二重周期、結び目は、振幅の周期変化をともなうぐるぐる
- 運動している本人たちにはどれも同じ。ぐるぐる回っているだけ。「外」から見ると違う。「外とは何か」…宇宙の研究をしているときに宇宙は紐なのか、というようなことを気にするのが「外」…
library(rgl)
t <- seq(from=0,to=1,length=1000)*2*pi
x <- sin(t)
y <- sin(t+2*pi/3)
z <- sin(t+4*pi/3)
xyz1 <- cbind(x,y,z)
matplot(xyz1,type="l")
plot3d(xyz1,type="l")
r1 <- 1
r2 <- 0.5
phi1 <- 2
phi2 <- 3
x <- r1 * cos(phi1*t) + r2 * cos(phi2*t)*cos(phi1*t)
y <- r1 * sin(phi1*t) + r2 * cos(phi2*t)*sin(phi1*t)
z <- r2 * sin(phi2*t)
xyz2 <- cbind(x,y,z)
matplot(xyz2,type="l")
plot3d(xyz2,type="l")
k1 <- 1
k2 <- k1*2
r1 <- 1/(2*(k1+k2))
r2 <- 1/(2*(k1-k2))
R <-1.5
r3 <- R/(k2)
phi1 <- k1+k2
phi2 <- k1-k2
phi3 <- k2
x <- r1 * sin(phi1*t) + r2 * sin(phi2*t) + r3 * sin(phi3*t)
y <- r1 * sin(phi1*(t+2*pi/3)) + r2 * sin(phi2*(t+2*pi/3)) + r3 * sin(phi3*(t+2*pi/3))
z <- r1 * sin(phi1*(t+4*pi/3)) + r2 * sin(phi2*(t+4*pi/3)) + r3 * sin(phi3*(t+4*pi/3))
xyz3 <- cbind(x,y,z)
matplot(xyz3,type="l")
plot3d(xyz3,type="l")
