2011-11-13

指数関数をいじる

こちらから
定数係数常微分方程式の中でも単純なもの
- - $y=e^{ax}$ が解だという
  - それは $\frac{d e^{ax}}{dx} = a e^{ax}$ だから
- なので
  - があるとき
    - $y=e^{a^{\frac{1}{k}} x}=e^{b_k x};b_k=a^{\frac{1}{k}}$ はその解である
- このとき
  - $\frac{d^i y}{dx^i}=a^{\frac{i}{k}}x=b_k^i x$
- 例えば、のときはの値によらず、
  - $\frac{d^i y}{dx^i} = b_k^i x$ で
  - $y=e^{ax}$
- $a \ne 1$ のときは、係数 $b_k^i$ が指数関数的に変化する
ここで、ある $a$ について、 $k$ が $y=e^{b_k x}$ の $b_k$ がどのように変化するのかを見てみよう

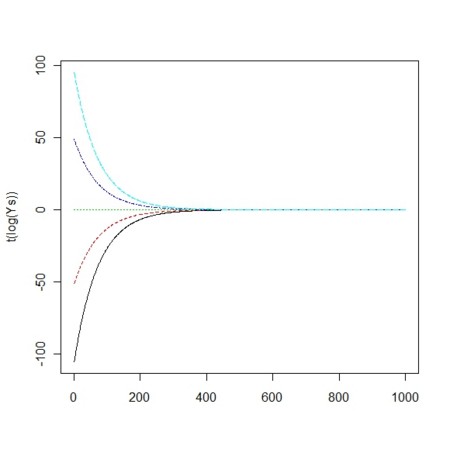
aRes<-seq(from=0.9, to=1.1, length=5)
logk<-seq(from=-3,to=3,length=1000)
k<-10^(logk)
Ys<-matrix(0,length(aRes),length(k))

for(ii in 1:length(aRes)){
	a<-aRes[ii]
	k.i<-a^(1/(k))
	X<-k
	Ys[ii,]<-k.i
}

matplot(t(log(Ys)),type="l")

今、は負でも構わない
- 上の図で $a=1$ の場合は、k(横軸)の値によらず、 $b_k$ が一定であった
- を考えてみよう
  - $y=e^{b_k x};b_k=(-1)^{\frac{1}{k}}$ である

# 複素数扱いにしよう
my1<-complex(real=1,imaginary=0)
myi<-complex(real=0,imaginary=-1)

a<-my1*(-1)

logk<-seq(from=-3,to=3,length=10000)
k<-10^(logk)
k.i<-a^(1/(k))
plot(Re(k.i))
plot(logk,log(Re(k.i)))

X<-k
Y<-Re(k.i)
Z<-Im(k.i)

library(rgl)
plot3d(log(X),Y,Z,type="p",cex=0.01)

この目でととを見よう
- は
  - $y=e^{(-1)^{\frac{1}{1}}x}=e^{-x}$
- は
  - $y=e^{(-1)^{\frac{1}{2}}x}=e^{ix}=\cos(x) + i \sin(x)$ だが、実数部分を取って、 $y=\cos(x)$ が見える部分
- ではは
  - $y=e^{(-1)^{\frac{1}{k}}x}=e^{(\cos(\frac{\pi}{k})+i\sin(\frac{\pi}{k}))x}=e^{x\cos(\frac{\pi}{k})}\times e^{i(x\sin(\frac{\pi}{k}))}$ となる。さらに $e^{i z}=\cos(z) + i \sin(z)$ だから
  - $y=e^{x\cos(\frac{\pi}{k})} \times(\cos(x\sin(\frac{\pi}{k}))+i \sin(x\sin(\frac{\pi}{k})))$
  - 実数部分と虚数部分を分ければ
    - $Re(y)=e^{x\cos(\frac{\pi}{k})} \times\cos(x\sin(\frac{\pi}{k}))$
    - $Im(y)=e^{x\cos(\frac{\pi}{k})} \times\sin(x\sin(\frac{\pi}{k}))$
  - 確かに、 $k=1$ のときには、 $Re(y)=e^{-x}$ となり、 $k=2$ のときには $Re(y)=cos(x)$ となっていて、OK
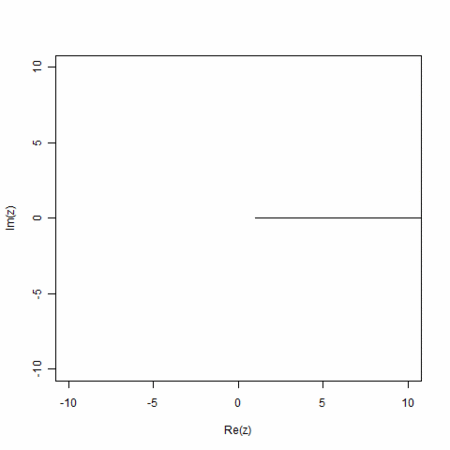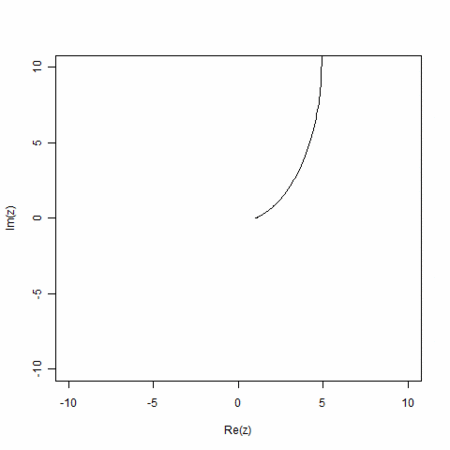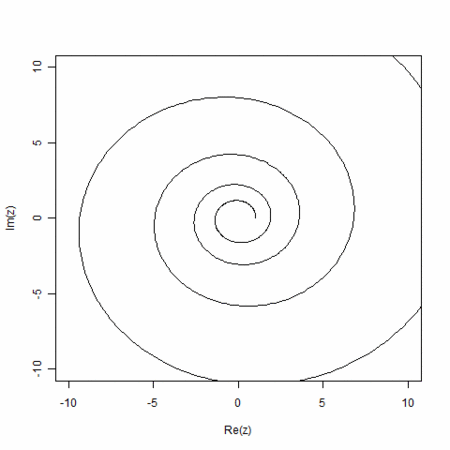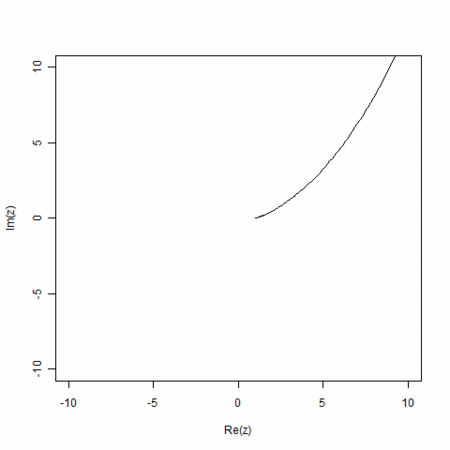
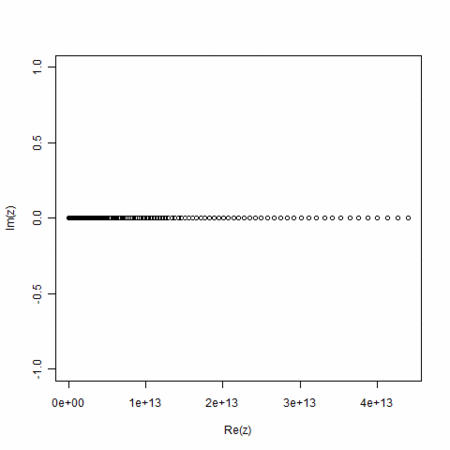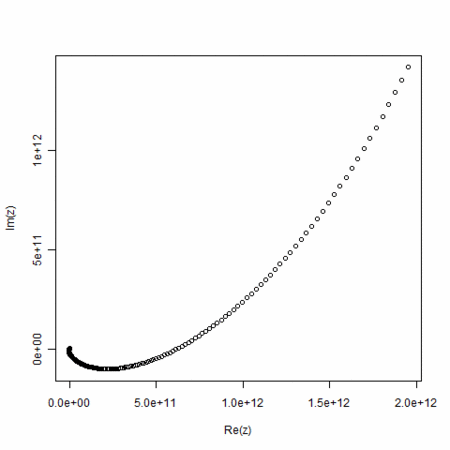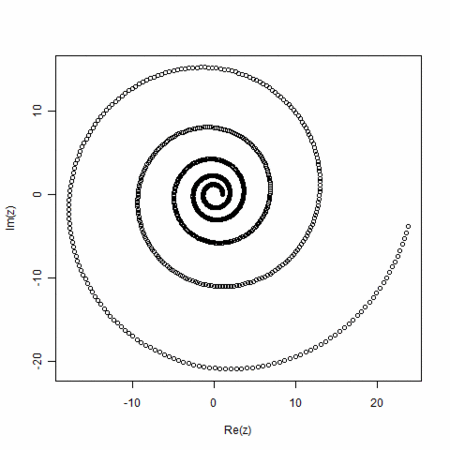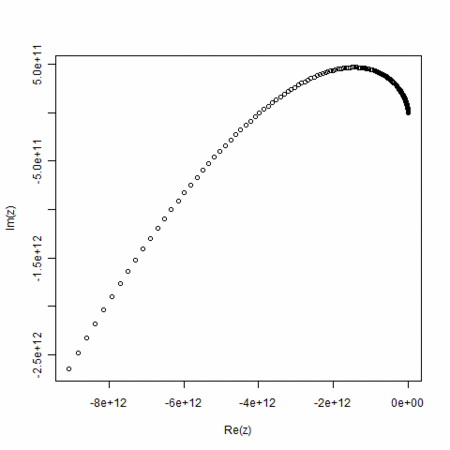
実直線上、単調減少かららせんを経て、円を通り、通り越して、らせん、その後、実直線上の単調増加へと変わる。曲率が無限大から、だんだん大きくなる状態、一定の状態、だんだん小さくなる状態へと移行する
$b_k$ は、 $k=1$ のときに複素平面で(-1,0)、 $k=2$ のときに(0,1)、大きくなるにつれ、(1,0)へと近づく
これは、 $e^{-x}$ から $e^{x}$ への変化。この２状態は、単調減少と単調増加。その間を結ぶ状態がらせん

logks<-seq(from=-1,to=1,by=0.01)
ks<-10^(logks)
x<-seq(from=0,to=1,length=1000)*2*pi*5
x<-as.complex(x)

Zs<-matrix(0,length(ks),length(x))

library(animation)
saveGIF({
for(ki in 1:length(ks)){
	k<-ks[ki]
	# 複素数扱いにしよう
	my1<-complex(real=1,imaginary=0)
	myi<-complex(real=0,imaginary=-1)

	a<-my1*(-1)

	y.re<-exp(cos(pi/k) * x)*cos(sin(pi/k)*x)
	y.im<-exp(cos(pi/2) * x)*sin(sin(pi/k)*x)

	#plot(x,y.re,type="l")
	#par(new=TRUE)
	#plot(x,y.im,col=2,type="l")

	z<-exp(a^(1/k)*x)
	Zs[ki,]<-z
	plot(z)

	#plot(y.re,Re(z))
	#plot(x,Re(z))

}

},interval=0.5)

の値を任意の複素数にもできる
- $b_k$ が負の実数のとき $k=2$ で円になる

logks<-seq(from=-1,to=1,by=0.1)
ks<-2^(logks)
x<-seq(from=0,to=1,length=1000)*2*pi*5
x<-as.complex(x)

Zs<-matrix(0,length(ks),length(x))

	a<-my1*(runif(1))+myi*(runif(1))
#a<-my1*(runif(1))*(-1)
for(ki in 1:length(ks)){
	k<-ks[ki]
	# 複素数扱いにしよう
	my1<-complex(real=1,imaginary=0)
	myi<-complex(real=0,imaginary=-1)


	y.re<-exp(cos(pi/k) * x)*cos(sin(pi/k)*x)
	y.im<-exp(cos(pi/2) * x)*sin(sin(pi/k)*x)

	#plot(x,y.re,type="l")
	#par(new=TRUE)
	#plot(x,y.im,col=2,type="l")

	z<-exp(a^(1/k)*x)
	Zs[ki,]<-z
	plot(z,xlim=c(-10,10),ylim=c(-10,10),type="l")

	#plot(y.re,Re(z))
	#plot(x,Re(z))
	Sys.sleep(0.7)
}

$\frac{d^k y}{dx^k} = -x$ を別の方法で考えてみる
$\frac{d \cos{t}}{dt}=-\sin{t}=-\cos{t+\frac{\pi}{2}$ なので、
$X_i=\cos(t+\frac{i}{2k}\pi)$ というような関数は
$\frac{d^{k+1} X_i}{dt^{k+1}}=-X_i$ となっていることがわかる
これは、 $\begin{pmatrix}0&-1&0&0&...&0\\ 0&0&-1&0&...&0\\...&...&...&...&...&...\\0&0&0&0&...&-1\\-1&0&0&0&...&0 \end{pmatrix}$ というような多変量の常微分連立方程式での関係の１表現(か)

t<-seq(from=0,to=1,length=1000)*2*pi*5
# 複素数扱いにしよう
my1<-complex(real=1,imaginary=0)
myi<-complex(real=0,imaginary=-1)

a<-(my1*(6))^(1/k)
k<-5
X<-matrix(0,k,length(t))
for(i in 1:k){
	X[i,]<-exp(myi*(a*t+i/(2*k)))
}

matplot(t(Re(X)),type="l")

plot(X[1,])