2013-10-18

駆け足で読む『A Guide to Mathematical Quasicrystals』

テキストはこちら
結構大変そう…
1. イントロ
- 準結晶を考えるときに、タイリングという考え方と点集合という考え方の２面がある
  - Delone setとして対称を捉える
    - 点の集合 $\Lambda$
    - Uniformly discrete(uniform minimal distance between the pointsが１個ある
    - Relatively dense(最大の穴が１つある…穴はあっても有限に抑えられている、と言うこと？)
  - タイリングとしてとらえる
    - ある空間を過不足なくタイル様のもので埋め尽くし
    - その上でそのタイルに(対称性を維持しながら)模様を入れる
    - これが作り上げるのがDelone set
  - Delone setがあったときボロノイ図を作ることができてそれはタイリングになっている。このボロノイ図的タイリングのdualはDeloneタイリング(ドロネー図のこと)(参考)
  - $\Lambda-\Lambda$ 「点集合のそれぞれの周りのテントのずれ」
  - 点集合で考えれば、点ペアのすべて、タイリングで考えればタイルのピース
  - 「ずれ」がdiscreteであるというのは、点の周りに空でない球がおけてその中に点がないようなこと
- 文書の構成
  - Non-crystallocraphic symmetries
  - Diffraction theory
  - Projection method
  - Minimal embedding
  - Local indistinguishability (local isomorphismとも)
  - Torus parametrization
  - Mutual local derivability (local equivalenceとも)
  - Inflation/deflation symmetries
  - Perfect matching rules
2. Non-crystallographic symmetries
- Lattice
  - Latticeはn次元実空間 $\mathbf{R}^n$ にある点の集合であって、n個の線形独立なベクトルの整数係数線形和で表されるもののこと( $\mathbf{R}^n /\Gamma$ がコンパクトであるように $\Gamma$ のこと、とも言う
- Periodic
  - Periodicとは0ベクトルでないベクトル $t$ があって、そのベクトルについて点の集合を並行移動したときに重なるような点集合のことをそう呼ぶ
  - またこのような $t$ のことをperiodと言う
- Crystallographic
  - LatticeがperiodicであるときCrystallographicと言う
- Crystallographic restriction
  - Crystallographicであるとき、回転に関する対称性があるが、格子点が整数係数のベクトル和で表されるという性質から、回転の角に制約がある。たとえば、n=1なら $2\pi,\pi$ の２通り、n=2,3なら $\frac{2\pi}{6},\frac{2\pi}{4},\frac{2\pi}{3},\frac{2\pi}{2},2\pi$ の５通り
- ある点集合・タイリングがcrystallographicでないことが、この回転制約からすぐわかる。平面のタイリング(点集合)が８重対称性があるとき、５通りで説明できないので、「これはCrystallographicでない」と言える
3. Diffraction 回折
- 格子・結晶があって、そこにX線を当てると解説という現象がおきて、２次元の点集合(的な)像が得られる。このようにしてX線を当てて得た像からもとの格子・結晶の構造を明らかにする分野があって、たくさんのことが知られている。この章はそのかいつまんだ、数学的構成の章
- 基本的には：
  - 格子・結晶を点集合と考えて、回折像も点集合と考える
  - 格子・結晶の点集合からフーリエ変換すると回折像の点重合になる
  - 点集合に周期性があるとき、「ずらすと重なる」という性質だ、とも言い換えられるが、そのようなときauto-correlationがあるとも言う。このauto-correlationの強さを表す関数もある
  - 点集合で考えるか、auto-correlationの関数で考えるかの２つのやり方がある
  - 結局、(点集合、auto-correlation関数)x(回折前、回折後)の２ｘ２＝４つの対象があって、その間に変換関係があることが数学的な話の枠である
  - ちなみに点集合を点集合に移す(回折像を取る)のがフーリエ変換、点集合とそれの別の味方であるauto-corrleation関数との関係はdual
- 点集合をDirac combと考える(ところどころにスパイク波がある関数)
  - $w_{\Lambda} = \sum_{x \in \Lambda} \delta_x$ 、ただし $\delta_x$ は点 $x$ におけるDirac(関数)の密度(分布)
- Auto-correlationはと表現する
  - ある半径 $r$ の球( $B_r$ の中にある格子上の２点 $x,y$ のずれが格子として適当なずれならカウントする、と言うルールで半径 $r$ の球を原点中心にとることにして、そんな格子点ペアがどれくらいの密度で存在するかを考えると、 $r\to \infty$ にしたときに極限があるという話
  - 離散的な場合、Dirac combの場合はこの極限の取り方も結構簡単に書き換えられる
- フーリエ変換はフーリエ変換
  - 便利さも含めてフーリエ変換
- Crystallographicな格子のフーリエ変換回折像でこのようになるのはよいとして、crystallographicでない格子の場合でフーリエ変換像が点集合にまとまる条件って・・・とか考え出すと、十分条件・必要条件で面倒が生じてきて、そこに登場するのが順結晶。回折像の対称性から「Crystallographicではないでしょう」とアカラサマにわかったりするので
4. Quasiperiodicity and the projection method
- 決して周期的でない関数
  - $sin(x)+sin(x+\tau)$ 、たとえば $\tau = \frac{1+\sqrt{5}}{2}$ は $\tau$ が無理数なので周期性はない
  - 周期性はないけれど、あるずれを入れると、そこそこ重なる関数はできて、しかもしの重なりのよいずれは、結構たくさんある
  - Rでやってみる
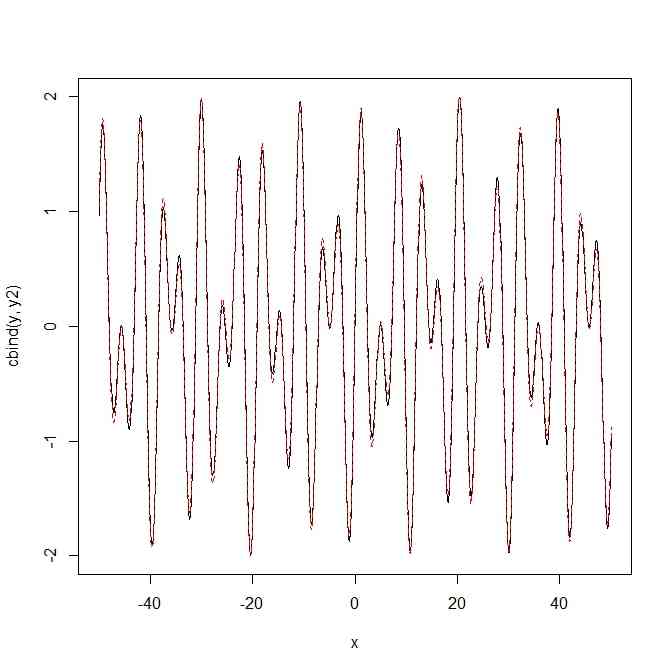
  - 確かにすごく近い

tau <- (1+sqrt(5))/2
#tau <- exp(1)
x <- seq(from=-50,to=50,length=1000)
y <- sin(x)+sin(tau*x)
# ずれを色々ためす
t <- seq(from=100,to=200,length=1000)
max.dis <- rep(0,length(t))
for(i in 1:length(t)){
	tmp.y <- sin(x+t[i])+sin(tau*(x+t[i]))
	max.dis[i] <- max(abs(y-tmp.y))
}
# ずれの値に対し、もっともずれている値をプロットすると、遠くなったり近くなったりする
plot(t,max.dis,type="l")
# 最大のずれが最小であるものを重ねて描いてみる
s <- which(max.dis==min(max.dis))[1]

y2 <- sin(x+t[s])+sin(tau*(x+t[s]))
matplot(x,cbind(y,y2),type="l")

- こんな風に十分確実に周期性ありっぽく扱えるような連続関数は三角関数の多項式近似がうまくいく
- そのことと、一般化したフーリエ級数と関係している(一般化したフーリエ級数というのは、２つの関数の積が積分すると0になるときその関数はお互いに直交しているというが、そういう直交した関数の級数展開のこと。普通のフーリエ級数に出てくるパーツ関数も『直交』している)
- この、周期性がないけれど周期性ありっぽく見える・ありっぽく扱える関数をquasiperiodicな関数と言う
- $f(x)=sin(x)+sin(y)|y=\tau x$ と書くと、周期関数 $sin(x)$ に、その周期関数に制約( $y=\tau x$ )を入れて、その制約ＯＫ分だけ付加したもの、と読める
- 周期的なものがあって、それに部分制約ＯＫだけをかぶせたものが準周期的なもの、というよう「意訳」できる
- この意訳(の一つ)がcut and projection法による準結晶生成
  - 高次元空間の次元を２つに分けて、一つは影を落とす空間、もう一つは影を作ることの許可を下す空間
  - こちらで実演
5. Minimal embedding and further examples
- ２次元の回折像が準結晶様であるとき、回折像の対称度から結晶格子がおさまる次元がいくつになるかは知られている