余る

• 双曲幾何を編み物で実現、という話(こちら)がある
• 双曲幾何の資料１
• Arithmetic hypervolic 3-manifold
• 双曲面はひらひらする
• ひらひらするのは「余」っているから
• 何が、どう、「余」っているのか
• 原点を中心に同心円を配置することを考える
• 半径の円の円周が、原点から平面的にの距離に配置するとすると、同心円は、平面上に並ぶ
• これが「同心円」による「平面」の作成法(鉤針編みでもうまくそうなるような眼の増やし方で編めば、円形コースターが編める)
• 半径の円が、原点から平面的にの距離より内側に置かなければならないとすると、「近すぎる」ので、その分を平面の外側(３次元空間の軸)に負担してもらわなければならない、そうして生じる面の曲がり方が、正の曲率で、その曲がり方が一定で続くとき、同心円の大きさには限度があって、最終的には球になる。
• 球面幾何
• 双曲幾何では、半径の円が、原点からの距離より外側に置かれることになるが、それを実現することは３次元空間でもできないので、原点から平面的にの距離のところに、円周がよりも長い円を配置することにする。半径のところにより長い周を置くには、余る長さを第３軸に負担してもらわなければならない。それが、双曲鉤針編みの「ひらひら」

• 負の曲率についての参考サイト(こちら)

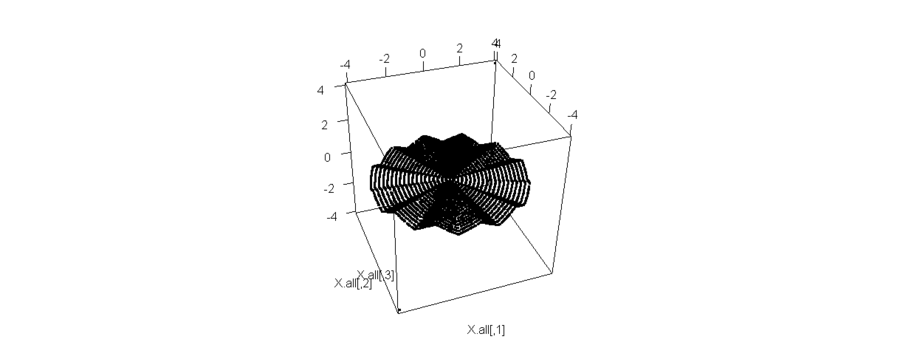
X <- list()
X.all <- matrix(0,0,3)
r <- seq(from=0,to=4,length=20)
k <- 0.01
n <- 12
N.r.pt <- 1000
for(i in 1:length(r)){
	t <- runif(N.r.pt)*2*pi
	X[[i]] <- matrix(0,length(t),3)
	X[[i]][,1] <- r[i] * cos(t)
	X[[i]][,2] <- r[i] * sin(t)
	incl.L <- 2*pi*r[i] * k
	incl.L.2 <- incl.L/(n*4)
	h <- sqrt(2*incl.L.2+incl.L^2)
	print(h)
	for(j in 1:length(t)){
		t.2 <- (t[j]%%((2*pi)/n))/(2*pi/n)
		if(t.2 < 0.5){
			X[[i]][j,3] <- h-(4*h*t.2)
		}else{
			X[[i]][j,3] <- -h+(4*h*(t.2-0.5))
		}
	}
	X.all <- rbind(X.all,X[[i]])
}
library(rgl)
X.all <- rbind(X.all,rep(max(X.all),3))
X.all <- rbind(X.all,rep(min(X.all),3))
plot3d(X.all)
rgl.snapshot("test.png")