2014-06-09

3. Path Curves in One and Two Dimenstions ぱらぱらめくる『The Vortex of Life』

ぱらぱらめくるシリーズ射影幾何 Collineation Polar opposite 極変換双対 R

１次元空間での射影変換は、第２次元の座標を加えてやって、２次元空間の点とした上で、線形変換をして１次元空間に戻してやる
不動点があるかどうか、その数が２個か１個か０個かは変換行列が決める
その具合により、Growth measure(成長尺、不動点が２個)、幾何的増加(指数関数的増加、不動点が１個と無限遠にもう１個)、Step measure(不動点が実重根)、循環尺(不動点が複素数(共役な２個))
１次元での変化は増えたり減ったり、収束したり循環したりを１次元空間上で起こす
２次元でのそれは２次元平面上の(曲)線になる
３次元空間での線形変換による軌道の写像である
３次元空間での軌道は、３次元の行列が決め、その様子は固有値の取り方で決まる。固有値が３つとも実数で異なるとき、固有値・固有ベクトルのペアが３つできる。それは２次元に対応付ければ、第３要素で第１・２要素を割った座標が対応する。その三角形の内部からの軌道はその三角形の内部しか動けない。なぜなら、この三角形の頂点とは不動だから。また、三角形の辺はその上しか動けないから。
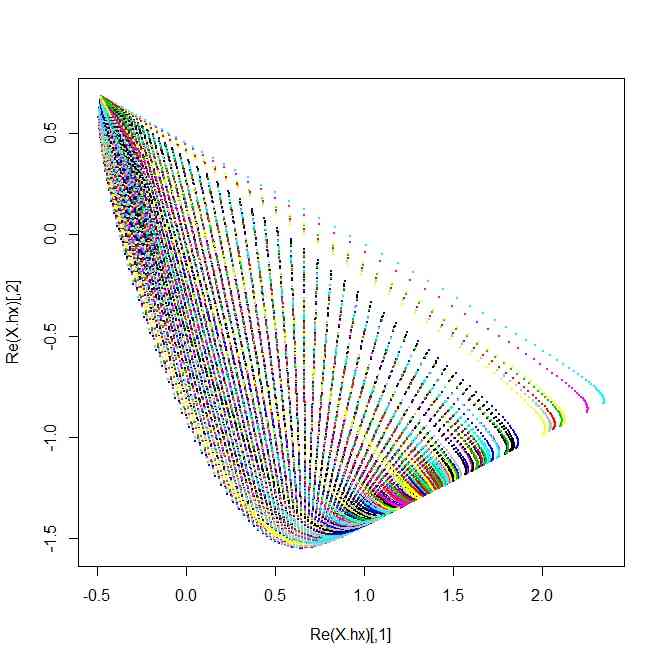
このことを使って、適当に固有値がすべて実数で異なる３ｘ３行列を作り、それの固有ベクトルを求め、その３次元固有ベクトルの２次元対応点を確認し、その３つの２次元対応点に囲まれた点を適当に発生させ、そこを通る軌道を作成すると、ハマグリのような形が得られる

# 指数行列
exp.m <- function(A,n){
	# 固有値分解
	eigen.out<-eigen(A)
	# P=V,P^{-1}=U
	V<-eigen.out[[2]]
	U<-solve(V)
	B<-diag(exp(eigen.out[[1]]*n))
	X <- V%*%B%*%U
	return(list(matrix = X, eigen.vs <- eigen.out[[1]]))
}
# d+1次元での連続軌道からd次元に戻す
my.pr.tr.cont <- function(x,M,t=seq(from=0,to=10,length=1000)){
	X <- c(x,1)
	out <- matrix(0,length(t),length(X))
	for(i in 1:length(t)){
		tmp <- exp.m(M,t[i])
		out[i,] <- tmp[[1]] %*% X
	}
	out2 <- out/out[,length(X)]
	out2[,-length(X)]
}
# 適当な回転行列を作る関数のためのパッケージ
library(GPArotation)
d <- 2 # 次元
R <- Random.Start(d+1)
# 適当な実数固有値を持たせる
M <- diag(c(2,3,4))
RM <- R %*% M
# 固有値分解
eigen.out <- eigen(RM)
# ３次元固有ベクトルを２次元対応点に変換
Vs <- t(eigen.out[[2]])
Vs <- t(Vs)/Vs[d+1,]
Vs <- Vs[1:d,]
# Dirichlet乱数を使って三角形内部の座標を得る
library(MCMCpack)
# 乱点数
n.iter <- 1000
RR <- rdirichlet(n.iter,rep(1,d+1))
# 各乱点を通る軌道の点の数
n <- 100
X.hx <- matrix(0,0,d)
t <- seq(from=-1,to=1,length=n)
for(ii in 1:n.iter){
x <- Vs[,1] + RR[ii,1] + Vs[,2]*RR[ii,2] + Vs[,3]*RR[ii,3]
X <- my.pr.tr.cont(x,RM,t)
X.hx <- rbind(X.hx,X)
}
plot(Re(X.hx),pch=20,cex=0.1,col=rep(1:n.iter,each=n))

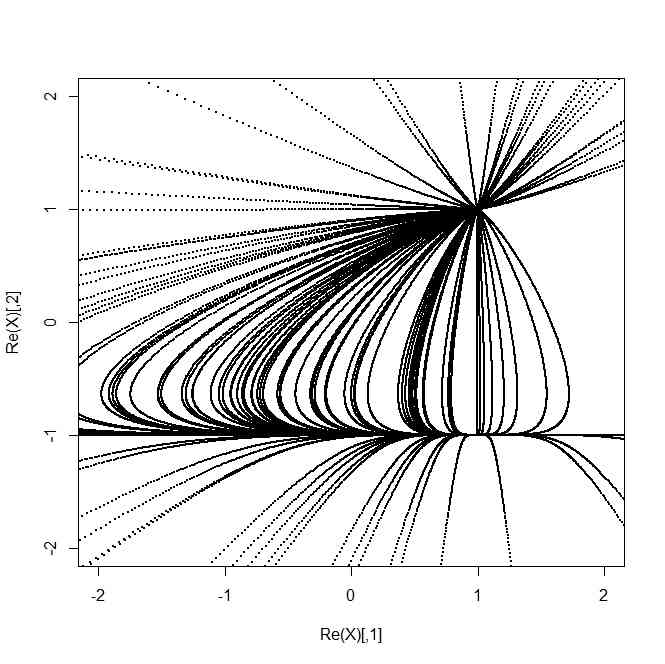
２次元の「栗」
- 不動点２点が有限、１点が無限だと、栗の平面版のようなものができる
- 二次元平面で(x1,y1),(x2,y2)を不動点、もう１点の不動点を無限遠にするに際し、第３座標を加えると、(x1,y1,1),(x2,y2,1),(x3,y3,0)にすればよい
- 今この３点を固有ベクトル(vi1,vi2,vi3)として、それぞれの固有値をkiとするような行列は
- $R \begin{pmatrix}v11 & v21 & v31 // v12 & v22 & v32 \\ v13 & v23 & v33 \end{pmatrix} = \begin{pmatrix}k1 v11 & k2 v21 & k3 v31 // k1 v12 & k2 v22 & k3 v32 // k1 v13 & k2 v23 & k3 v33 /end{pmatrxi}$ となればよいから、それを解いてRを求めてやることにする

# 固有値
ks <- c(0.8,-0.3,0.6)
# 固有ベクトル
vs <- matrix(c(1,-1,1,1,1,1,0.5,0,0),3,3)
Vs <- t(t(vs) * ks)
vs
Vs
R <- Vs %*% solve(vs)
R
eigen.out <- eigen(R)
eigen.out

n.iter <- 100
t <- seq(from=-10,to=10,length=1000)
X <- matrix(0,0,2)
for(i in 1:n.iter){
	tmp <- rnorm(2)*1
	tmpX <- my.pr.tr.cont(tmp,R,t)
	X <- rbind(X,tmpX)
}
plot(Re(X),pch=20,cex=0.1,xlim=c(-2,2),ylim=c(-2,2))