ggplot2を使ったお絵かき遊び

• 多(２)次元正規分布の混成でできているような分布が２つある
• 分布は場所によって、片方の分布から発生しやすかったり、逆にもう片方の分布から発生しやすかったりする
• それは尤度比
• そんなことを理論値や標本からの推定値でプロットしてみる

library(pracma)
library(MCMCpack)
library(ggplot2)
# 多次元複合分布を作ろう
# 次元
k <- 2
# No. 正規分布
n <- 8

# 正規分布のパラメタ
#centers <- rdirichlet(n,rep(1,k))
centers <- matrix(runif(n*k),ncol=k)
sds <- list()
for(i in 1:n){
	tmp <- t(rdirichlet(k,rep(1,100)))
	sds[[i]] <- cov(tmp)
	sds[[i]] <- sds[[i]]/sum(sds[[i]])*0.05
}

# No. 群
ng <- 2

# 群ごとの正規分布混合割合
library(mvtnorm)
ratios <- matrix(0, ng,n)
for(i in 1:ng){
	ratios[i,] <- rdirichlet(1, rdirichlet(1,rep(1,n)*10))
}
ratios <- rdirichlet(ng, rep(1,n))

# 分布ごとの位置別の確率
x <- list(seq(from = -2, to = 3, length = 100))
X <- expand.grid(rep(x,k))

D <- list()
for(i in 1:n){
	D[[i]] <- apply(X, 1, dmvnorm, mean = centers[i,], sigma = sds[[i]])
}

# 群ごとの位置別の確率
D.g <- list()
for(i in 1:ng){
	D.g[[i]] <- rep(0,length(D[[1]]))
	for(j in 1:n){
		D.g[[i]] <- D.g[[i]] + ratios[i,j] * D[[j]]
	}
}

par(mfcol=c(1,2))
image(matrix(D.g[[1]],length(x[[1]]),length(x[[1]])))
image(matrix(D.g[[2]],length(x[[1]]),length(x[[1]])))
par(mfcol=c(1,1))

df1 <- data.frame(x=rep(X[,1],2),y=rep(X[,2],2),z=c(D.g[[1]],D.g[[2]]),gr=factor(c(rep(1,length(X[,1])),rep(2,length(X[,1])))))
#df2 <- data.frame(x=X[,1],y=X[,2],z=D.g[[2]])
v <- ggplot(df1, aes(x, y, z = z)) 
v +geom_tile(aes(fill=z)) + scale_fill_gradient(low="green", high="red")+ stat_contour() + facet_wrap(~ gr)


# 群ごとに乱点を発生させよう

df <- data.frame(x=c(R[[1]][,1],R[[2]][,1]),y=c(R[[1]][,2],R[[2]][,2]),gr = c(rep(1,Npt[1]+n),rep(2,Npt[2]+n)))


gp <- ggplot(df,aes(x=x,y=y,colour = factor(gr))) + geom_point(alpha=0.3)
gp

# Likelihood ratioを計算しよう
# 片方の群の乱点からいくつか選んで、そこの尤度比を計算する
selected <- sample(1:length(R[[1]][,1]),100)

LR <- rep(0,length(selected))
LR.gauss <- LR
for(i in 1:length(LR)){
	LR[i] <- likelihoodratio.roc.kernel(R[[1]],R[[2]],c(R[[1]][selected[i],]),kernel="g")$dens.0
	LR.gauss[i] <- likelihoodratio.gauss(R[[1]],R[[2]],c(R[[1]][selected[i],]))$LR
}

df.new <- data.frame(x=R[[1]][selected,1],y=R[[1]][selected,2],z=LR)

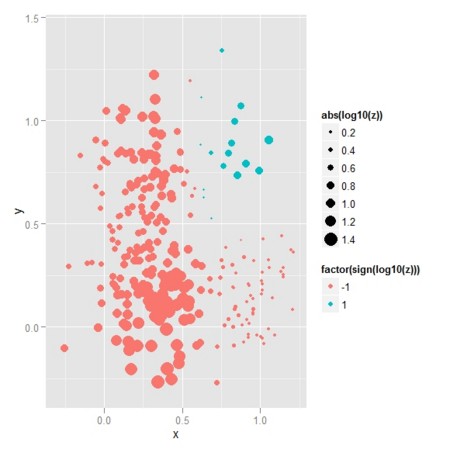
ggg <- ggplot(data = df.new,aes(x=x,y=y,size=abs(log10(z)),colour=factor(sign(log10(z))))) + geom_point()
ggg

df.new.gauss <- data.frame(x=R[[1]][selected,1],y=R[[1]][selected,2],z=LR.gauss)

ggg.gauss <- ggplot(data = df.new.gauss,aes(x=x,y=y,size=abs(log10(z)),colour=factor(sign(log10(z))))) + geom_point()
dev.new()
ggg.gauss


dev.new()
gp <- ggplot(df,aes(x=x,y=y)) + geom_point(alpha=0.3) + facet_wrap(~ gr)
gp

D.1 <- list()
for(i in 1:n){
	D.1[[i]] <- apply(R[[1]][selected,], 1, dmvnorm, mean = centers[i,], sigma = sds[[i]])
}

# 群ごとの位置別の確率
# 選んだ点について、理論的な尤度比を計算する
D.g.1 <- list()
for(i in 1:ng){
	D.g.1[[i]] <- rep(0,length(D.1[[1]]))
	for(j in 1:n){
		D.g.1[[i]] <- D.g.1[[i]] + ratios[i,j] * D.1[[j]]
	}
}

D.g.1.ratio <- D.g.1[[2]]/D.g.1[[1]]

dev.new()
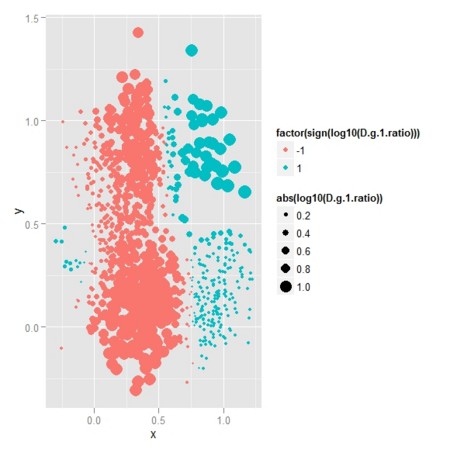
ggg.2 <- ggplot(data = df.new,aes(x=x,y=y,size=abs(log10(D.g.1.ratio)),colour=factor(sign(log10(D.g.1.ratio))))) + geom_point()
ggg.2


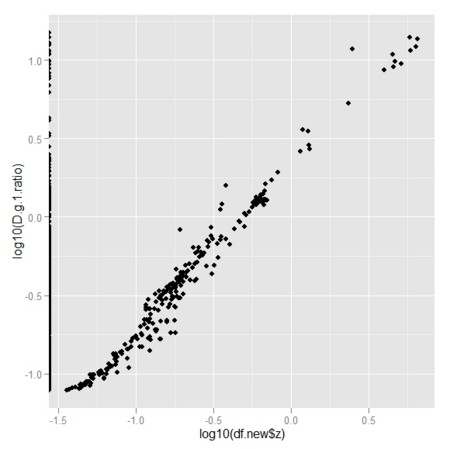
qplot(log10(df.new$z),log10(D.g.1.ratio))

• ２つの分布

• 乱点標本

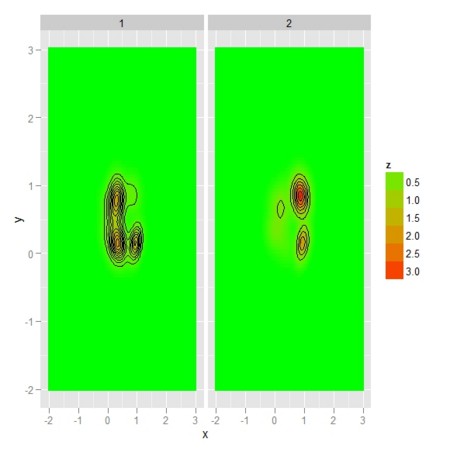
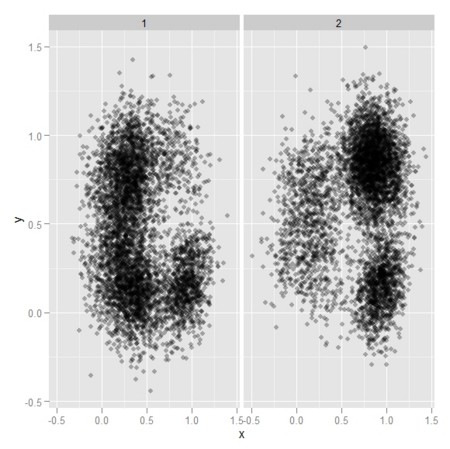
• 理論的尤度比(２色は、どちらの群が優位かを表し、点のサイズは尤度比の差の大きさを表す)

• 標本から尤度比を推定して同様にプロット

• 理論値と標本からの推定値の一致具合

• 以下、やっつけ関数群

library(sde)
library(pracma)
k <-2
c1 <- rep(0,k)

c2 <- c(1,rep(0,k-1))

x <- y <- seq(from=-2,to=3,by=pi/30)
xy <- expand.grid(x,y)

sd1 <- 0.5
sd2 <- 0.7
Npt <- 10000
A.1 <- matrix(rnorm(Npt*k,sd=sd1),ncol=k)
A.2 <- matrix(rnorm(Npt*k,sd=sd2),ncol=k)
A.2[,1] <- A.2[,1]+c2[1]

my.A <- data.frame(x=c(A.1[,1],A.2[,1]),y=c(A.1[,2],A.2[,2]),group= c(rep(1,length(A.1[,1])),rep(2,length(A.2[,1]))))

gp <- ggplot(data = my.A)
gp <- gp + aes(x=x,y=y,colour=factor(group)) + geom_point(alpha=0.3)
gp

dens.calc <- function(x,t){
	y <- t(t(x)-t)
	r <- sqrt(apply(y^2,1,sum))
	n <- length(x[1,])
	s <- Sphere.surface(n-1,r)
	return(list(r=r,s=s))
}

Sphere.surface <- function(n, r){
	2*pi^((n+1)/2) / gamma((n+1)/2) * r^n
}
my.roc<-function(x,y,t=NULL){
	Nx <- length(x)
	Ny <- length(y)
	if(is.null(t))t<-seq(from=min(x,y),to=max(x,y),length=100)
	xa<-outer(x,t,FUN="<")
	ya<-outer(y,t,FUN="<")
	xb<-apply(sign(xa),2,sum)
	yb<-apply(sign(ya),2,sum)

	xy<-data.frame(X=Nx-xb,Y=Ny-yb)
	return(xy)
}
my.roc.2<-function(x,y,t=NULL){
	Nx <- length(x)
	Ny <- length(y)
	if(is.null(t))t<-seq(from=min(x,y),to=max(x,y),length=100)
	xa<-outer(x,t,FUN="<")
	ya<-outer(y,t,FUN="<")
	xb<-apply(sign(xa),2,sum)
	yb<-apply(sign(ya),2,sum)
	X<-Nx-xb
	Y<-Ny-yb
	X.1<-(X-min(X))/(max(X)-min(X)) *2-1
	Y.1<-(Y-min(Y))/(max(Y)-min(Y)) *2-1

	xy<-data.frame(X=X.1,Y=Y.1)
	return(xy)
}

# Function to estimate polynomial coefficients and coordinates estimated
# 多項式近似の係数と、推定座標を返す関数
glmPolynomial<-function(y,x,dg){# y:dependent values (従属値列),x:descriptive values (説明変数),dg:degrees of polynomials (多項式の次数)
 # Xs: Matrix consisted of x^1,x^2,...x^{dg}
 # Xs: xの1,2,...,dg 乗の値でできた行列
 Xs<-matrix(0,length(x),dg) 
 for(i in 1:dg){
  Xs[,i]<-x^i
 }
 # glm() is generalized linear regression function in R
 # glm() はＲの一般化線形回帰関数
 fit<-glm(y~Xs[,1:dg]) 
 # beta: coefficients estimated
 # beta: 推定係数ベクトル
 beta<-fit$coefficients
 # Xs2 has an additional column for x^0
 # Xs2 には、x^0のための列を追加
 Xs2<-cbind(rep(1,length(x)),Xs)
 # predY is a matrix of values for individual degrees of x
 # predY は xの各次数の項
 predY<-t(t(Xs2)*beta)
 # apply(): Sum up all columns corresponding to 0 to dg degrees
 # apply()関数で0:dg次数のすべてを足し合わせる
 sumupPredY<-apply(predY,1,sum)
 list(beta=beta,x=x,predY=sumupPredY)
}

# 多項式近似して、その傾きを返す
poly.grad <- function(y,x,dg,t){
	glmpoly <- glmPolynomial(y,x,dg)
	ret <- rep(0,length(t))
	for(i in 1:(dg-1)){
		ret <- ret + glmpoly$beta[i+1]*i*t^(i-1)
	}
	list(glmpoly=glmpoly,deriv=ret)
}
# Generate data
x<-sort(runif(100))
y<-runif(100)+x^3*2+x^4*5

xlim<-c(min(x),max(x))
ylim<-c(min(y),max(y))
plot(x,y,xlim=xlim,ylim=ylim,col="red")

# GLM is to be applied to multiple degrees (dgs)
# GLMを複数の次数に適用
dgs<-1:5
for(i in dgs){
 outglm<-glmPolynomial(y,x,i)
 par(new=TRUE)
 # gray() changes contrast 
 # gray() 関数は線の濃淡を変える
 plot(outglm$x,outglm$predY,xlim=xlim,ylim=ylim,col=gray(i/(max(dgs)*1.5)),type="l")
}

# 多項式近似をして、係数を取り出し、それに基づいて「微分して」
tmp.fx <- function(A.1,A.2,P,npt = 512, theta=pi/6,deg=8,deriv.pt=NULL){
	# ２群の点と、着目点とのユークリッド距離の分布をとる
	# 距離0が「着目点」の位置

	d1 <- dens.calc(A.1,P)
	d2 <- dens.calc(A.2,P)
	# 鏡像分布
	R1 <- c(d1$r,-d1$r)
	R2 <- c(d2$r,-d2$r)
	
	t.2 <- seq(from=min(R1,R2),to=max(R1,R2),length=npt)
	my.roc.out <- my.roc.2(R1,R2,t.2)
	out.df <- data.frame(thres=t.2,roc.x=my.roc.out$X,roc.y=my.roc.out$Y)
	myroc.df <- data.frame(x=my.roc.out$X,y=my.roc.out$Y)
	#plot(myroc.df)
	gg.roc <- ggplot(data=myroc.df,aes(x=x,y=y))
	gg.roc <- gg.roc + geom_point() + stat_smooth()
	#dev.new()
	#gg.roc
	# 角変更
	M <- matrix(c(cos(theta),cos(pi/2-theta),sin(theta),sin(pi/2-theta)),byrow=TRUE,2,2)

	new.XY<-t(M%*%t(as.matrix(myroc.df)))
	out.df$roc.x.rotated=new.XY[,1]
	out.df$roc.y.rotated=new.XY[,2]
	
	new.XY.df <- data.frame(x=new.XY[,1],y=new.XY[,2])
	#gg.roc.new <- ggplot(data=new.XY.df,aes(x=x,y=y))
	#gg.roc.new <- gg.roc.new + geom_point() + stat_smooth()
	#dev.new()
	#gg.roc.new
	#Han <- function(y) # Hanning
  #     convolve(y, c(1,2,1)/4, type = "filter")
	#dev.new()
	#plot(new.XY.df$x,new.XY.df$y, main="Using  convolve(.) for Hanning filters")
	n<-length(new.XY.df$x)
	#lines(new.XY.df$x[-c(1  , n)      ], Han(new.XY.df$y), col="red")
	#lines(new.XY.df$x[-c(1:2, (n-1):n)], Han(Han(new.XY.df$y)), lwd=2, col="dark blue")
	#	xi <- seq(from=min(x),to=max(x), len = 81)
	#yl <- interp1(x, y, xi, method = "linear")

	## Not run: 
	#plot(x, y); grid()
	#lines(xi, yl, col="blue", lwd = 2)
	#x <- new.XY.df$x
	#y <- new.XY.df$y
	x <- out.df$roc.x.rotated
	y <- out.df$roc.y.rotated
	
	#outglm<-glmPolynomial(y,x,deg)
	#print(outglm)
	# gray() changes contrast 
	# gray() 関数は線の濃淡を変える
	#dev.new()
	#plot(x, y); grid()

	#lines(outglm$x,outglm$predY,col="blue", lwd = 2)
	#print(outglm$beta)
	if(is.null(deriv.pt)){
		deriv.pt <- sort(c(x,0))
	}
	#print(deriv.pt)
	poly.grad.out <- poly.grad(y,x,deg,deriv.pt)
	
	glmpoly <- poly.grad.out$glmpoly
	
	beta<-glmpoly$beta
	out.df$approx.x.rotated <- glmpoly$x
	out.df$approx.y.rotated <- glmpoly$predY
	
	grad.df <- data.frame(grad.x=deriv.pt,grad.rotated=poly.grad.out$deriv)
	
	#dev.new()
	df.poly <- data.frame
	#gg.poly <- ggplot(data=new.XY.df,aes(x=x,y=y))
	#gg.poly <- gg.poly + geom_point()
	#gg.poly <- gg.poly + geom_line(x=poly.grad.out$glmpoly$x,y=poly.grad.out$glmpoly$predY)
	#gg.poly
	#plot(x,poly.grad.out$deriv)
	
	# 傾きを元に戻す
	phi <- atan(grad.df$grad.rotated)
	grad.df$phi.rotated <- phi
	phi<-(phi-pi/4)*(pi/4)/(pi/4-theta)+pi/4
	grad.df$phi <- phi
	
	#dev.new()
	#plot(x,phi)
	#return(list(data=list(A.1=A.1,A.2=A.2),P=P,theta=theta,deg=deg,deriv.pt=deriv.pt,dens=list(d1=d1,d2=d2),gg.roc=gg.roc,gg.roc.new=gg.roc.new,poly.grad.out=poly.grad.out,phi=phi))
	return(list(data.df = out.df,grad.df=grad.df,poly.beta=beta))
}
likelihoodratio.roc.poly <- function(A.1,A.2,P,npt = 512, theta=pi/6,deg=8,deriv.pt=NULL){
	# ２群の点と、着目点とのユークリッド距離の分布をとる
	# 距離0が「着目点」の位置

	d1 <- dens.calc(A.1,P)
	d2 <- dens.calc(A.2,P)
	# 鏡像分布
	R1 <- c(d1$r,-d1$r)
	R2 <- c(d2$r,-d2$r)
	
	t.2 <- seq(from=min(R1,R2),to=max(R1,R2),length=npt)
	my.roc.out <- my.roc.2(R1,R2,t.2)
	out.df <- data.frame(thres=t.2,roc.x=my.roc.out$X,roc.y=my.roc.out$Y)
	myroc.df <- data.frame(x=my.roc.out$X,y=my.roc.out$Y)
	# 角変更
	M <- matrix(c(cos(theta),cos(pi/2-theta),sin(theta),sin(pi/2-theta)),byrow=TRUE,2,2)

	new.XY<-t(M%*%t(as.matrix(myroc.df)))
	out.df$roc.x.rotated=new.XY[,1]
	out.df$roc.y.rotated=new.XY[,2]
	
	new.XY.df <- data.frame(x=new.XY[,1],y=new.XY[,2])

	x <- out.df$roc.x.rotated
	y <- out.df$roc.y.rotated
	

	if(is.null(deriv.pt)){
		deriv.pt <- sort(c(x,0))
	}
	poly.grad.out <- poly.grad(y,x,deg,deriv.pt)
	
	glmpoly <- poly.grad.out$glmpoly
	
	beta<-glmpoly$beta
	out.df$approx.x.rotated <- glmpoly$x
	out.df$approx.y.rotated <- glmpoly$predY
	
	grad.df <- data.frame(grad.x=deriv.pt,grad.rotated=poly.grad.out$deriv)
	
	df.poly <- data.frame
	
	# 傾きを元に戻す
	phi <- atan(grad.df$grad.rotated)
	grad.df$phi.rotated <- phi
	phi<-(phi-pi/4)*(pi/4)/(pi/4-theta)+pi/4
	grad.df$phi <- phi
	
	return(list(data.df = out.df,grad.df=grad.df,poly.beta=beta))
}


#t.out <- tmp.fx(A.1,A.2,rep(0,k),theta=pi/10,deg=8)
t.out <- tmp.fx(A.1,A.2,rep(0,k),theta=pi/10,deg=8,npt=10^4,deriv.pt=seq(from=-1,to=1,length=513))
#t.out <- tmp.fx(A.1,A.2,rep(0,k),theta=pi/10,deg=8,deriv.pt=seq(from=-1,to=1,length=10))

gg.1 <- ggplot(data=t.out$data.df, aes(x=roc.x,y=roc.y)) + geom_point()
gg.1

gg.2 <- ggplot(data=t.out$data.df, aes(x=roc.x.rotated,y=roc.y.rotated)) + geom_point()
gg.2

gg.3 <- ggplot(data=t.out$data.df, aes(x=approx.x.rotated,y=approx.y.rotated)) + geom_point()
gg.3

gg.4 <- ggplot(data=t.out$grad.df, aes(x=grad.x,y=grad.rotated)) + geom_point()
gg.4

gg.5 <- ggplot(data=t.out$grad.df, aes(x=grad.x,y=phi.rotated)) + geom_point()
gg.5

gg.6 <- ggplot(data=t.out$grad.df, aes(x=grad.x,y=phi)) + geom_point()
gg.6

gg.7 <- ggplot(data=t.out$grad.df, aes(x=grad.x,y=tan(phi))) + geom_point()
gg.7


tan(t.out$grad.df$phi[which(t.out$grad.df$grad.x==0)])

likelihoodratio.roc.kernel <- function(A.1,A.2,P,npt.roc = 1000,npt.kernel = 10^6, density.npt = 513,kernel= c("gaussian", "epanechnikov", "rectangular","triangular", "biweight","cosine", "optcosine")){
	# ２群の点と、着目点とのユークリッド距離の分布をとる
	# 距離0が「着目点」の位置

	d1 <- dens.calc(A.1,P)
	d2 <- dens.calc(A.2,P)
	# 鏡像分布
	R1 <- c(d1$r,-d1$r)
	R2 <- c(d2$r,-d2$r)
	
	t <- seq(from=min(R1,R2),to=max(R1,R2),length=npt.roc)
	my.roc.out <- my.roc.2(R1,R2,t)
	
	x <- my.roc.out$X
	y <- my.roc.out$Y
	
	yi<-seq(from=range(y)[1],to=range(y)[2],length=npt.kernel)
	xc<-interp1(y,x,yi,method="constant")

	density.out <- density(xc,n=density.npt,from=-1,to=1,kernel=kernel)


	
	return(list(roc.df = data.frame(t=t,x=x,y=y),interpor.roc.df = data.frame(x=xc,y=yi),density.out=density.out,dens.0=density.out$y[which(density.out$x==0)]))
}

# でもそんなことをしなくても、尤度比を出すだけなら、これでもよい
likelihoodratio.gauss <- function(A.1,A.2,P){
	# ２群の点と、着目点とのユークリッド距離の分布をとる
	# 距離0が「着目点」の位置

	d1 <- dens.calc(A.1,P)
	d2 <- dens.calc(A.2,P)
	# 距離の２乗
	R1 <- d1$r^2
	R2 <- d2$r^2
	
	Prob1 <- sum(exp(-R1))/length(R1)
	Prob2 <- sum(exp(-R2))/length(R2)
	
	return(list(pr.1 = Prob1, pr.2 = Prob2, LR = Prob1/Prob2))
}